
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения с разделяющимися переменными
Простейшим дифференциальным уравнением первого порядка (Д.У. – I) является уравнение вида 
 или
или  Как известно из курса интегрального исчисления, функция у находится интегрированием
Как известно из курса интегрального исчисления, функция у находится интегрированием 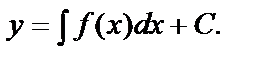
Уравнение вида 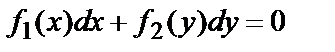 называется дифференциальным уравнением с разделёнными переменными. Это видно, если одно из слагаемых перенести в правую часть:
называется дифференциальным уравнением с разделёнными переменными. Это видно, если одно из слагаемых перенести в правую часть:

Проинтегрируем обе части последнего уравнения и получим так называемый общий интеграл (или общее решение)

Пример. Найти частное решение уравнения 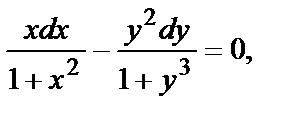 удовлетворяющее условию
удовлетворяющее условию 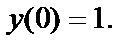
Решение: Запишем уравнение в виде 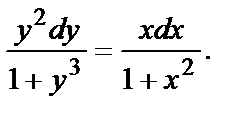 Проинтегрируем обе части и учтём постоянную интегрирования
Проинтегрируем обе части и учтём постоянную интегрирования 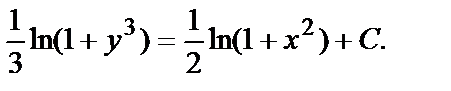
В полученный общий интеграл подставим данное начальное условие 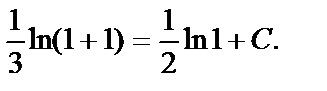 Отсюда
Отсюда 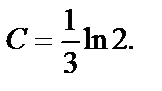 Искомое частное решение (или частный интеграл):
Искомое частное решение (или частный интеграл):
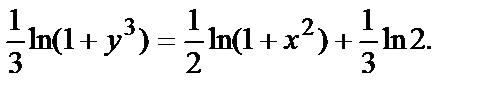
Можно упростить полученный интеграл, умножив на 6 и пропотенцировав



Заметим, что общее решение или частное решение может иметь различные формы. Правильность решения нужно доказать проверкой. В нашем случае докажем, что частный интеграл  получен правильно. Для этого продифференцируем обе части полученного равенства и из системы двух уравнений, из которых одно – полученный частный интеграл, а другое – результат его дифференцирования, получим дифференциальное уравнение, предложенное для решения.
получен правильно. Для этого продифференцируем обе части полученного равенства и из системы двух уравнений, из которых одно – полученный частный интеграл, а другое – результат его дифференцирования, получим дифференциальное уравнение, предложенное для решения.

упростим полученное равенство и запишем систему
| { | 

|
Подставив в первое уравнение выражение для 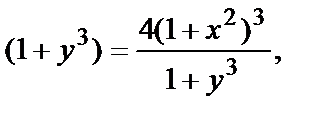 полученное из второго уравнения, имеем
полученное из второго уравнения, имеем 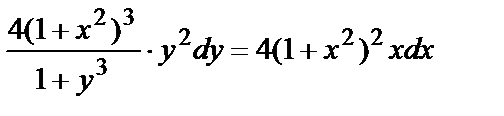 или
или  — данное Д.У..
— данное Д.У..
Определение. Уравнение вида  называется уравнением с разделяющимися переменными, если выражения
называется уравнением с разделяющимися переменными, если выражения  и
и 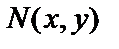 можно представить в виде произведения функций
можно представить в виде произведения функций
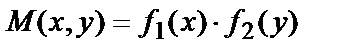 и
и

Чтобы решить такое Д.У., необходимо привести его к виду Д.У. с разделёнными переменными, для чего разделим на произведение 
Действительно, разделив все члены уравнения

на произведение 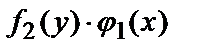 , получим
, получим
 -
-
Д.У. с разделёнными переменными. Для решения его достаточно проинтегрировать обе части уравнения

 - общий интеграл Д.У..
- общий интеграл Д.У..
При решении Д.У. с разделяющимися переменными надо знать
Правило разделения переменных:
Первый шаг. Если Д.У. содержит производную, её следует записать в виде отношения дифференциалов 

Второй шаг. Умножив на дифференциал независимой переменной (dx), сгруппировать слагаемые, содержащие дифференциал функции и дифференциал независимой переменной (dy и dx).
Третий шаг. Выражения, полученные при dy и при dx представить в виде произведения двух множителей, каждый из которых содержит только одну переменную (либо y, либо x). Если после этого уравнение примет вид
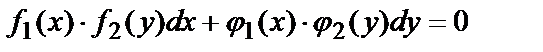
то разделив на произведение 
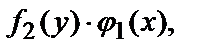 уравнение приводим к уравнению с разделёнными переменными.
уравнение приводим к уравнению с разделёнными переменными.
Четвёртый шаг. Интегрируя каждую часть уравнения, получим общее решение исходного уравнения (или его общий интеграл)
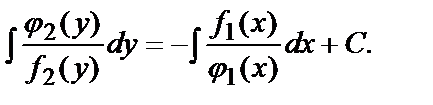
Например, рассмотрим уравнения
№ 1. 
№ 2. 
№ 3. 
Укажем, какие из них являются Д.У. с разделяющимися переменными.
Д.У. № 1 легко приводится к виду

Разделив на 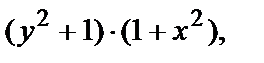 получим
получим 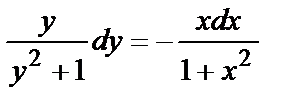 - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.
В Д.У. № 2 заменим 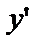 на
на 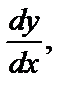 умножим на
умножим на  , получим
, получим
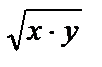 +
+ 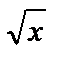


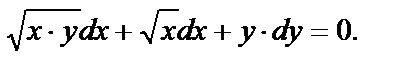
Сгруппировав первые два слагаемые, сразу вынесем за скобку множитель 
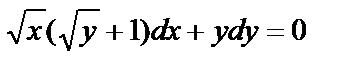 - уравнение с разделяющимися переменными. Разделив на
- уравнение с разделяющимися переменными. Разделив на  получим
получим 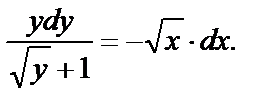
Уравнение №3 не может быть уравнением с разделяющимися переменными, т.к. записав его в виде 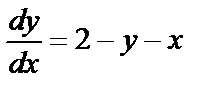 или
или  видим, что выражение
видим, что выражение  в виде произведения двух множителей (один – только с у, другой – только с х) представить невозможно.
в виде произведения двух множителей (один – только с у, другой – только с х) представить невозможно.
Заметим, что иногда нужно выполнить алгебраические преобразования, чтобы видеть, что данное Д.У. – с разделяющимися переменными.
Рассмотрим следующие Д.У.:
№4. 

Применим известную формулу

получим  или
или 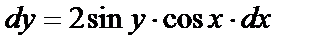 - уравнение с разделяющимися переменными. Разделив на sin y, получим
- уравнение с разделяющимися переменными. Разделив на sin y, получим 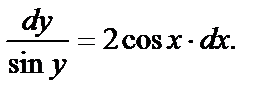 Интегрируя, получим общий интеграл
Интегрируя, получим общий интеграл
 или
или 
Можно использовать определение логарифма и записать общий интеграл в виде  (а)
(а)
Заметим, что общий интеграл данного Д.У. можно получить иначе, если постоянную интегрирования записать в виде 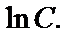 Тогда после интегрирования Д.У. общий интеграл примет вид
Тогда после интегрирования Д.У. общий интеграл примет вид

 (б)
(б)
Таким образом, общий интеграл одного и того же Д.У. может иметь различную форму. Важно в любом случае доказать, что полученный Вами общий интеграл удовлетворяет данному Д.У.. Сделаем проверку для Д.У. №4 и покажем, что и форма (а), и форма (б) общего интеграла верна.
Если в случае (а) общий интеграл 
 , то продифференцировав по х обе части этого равенства, запишем систему:
, то продифференцировав по х обе части этого равенства, запишем систему:

Исключив выражение  , получим
, получим 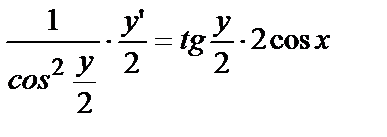 или
или 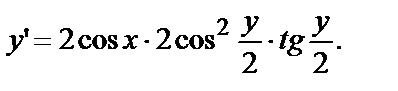
Используя формулы: 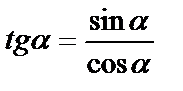 и
и  получаем Д.У.
получаем Д.У.

В случае (б) общий интеграл 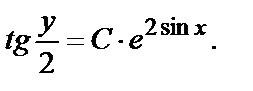 Продифференцируем это равенство по х и исключим выражение, содержащее С, из системы.
Продифференцируем это равенство по х и исключим выражение, содержащее С, из системы.
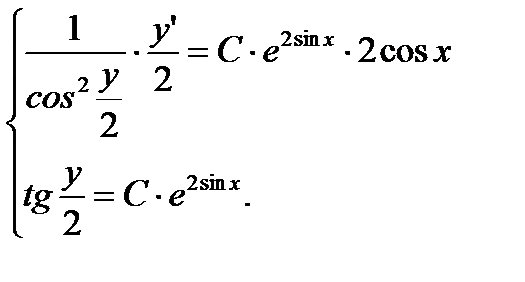
Получим 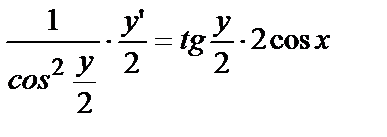 — то же уравнение, что и в случае (а).
— то же уравнение, что и в случае (а).
Найдём общее решение для Д.У..
№5. 

Умножив обе части уравнения на дробь  получим уравнение с разделенными переменными
получим уравнение с разделенными переменными  или
или
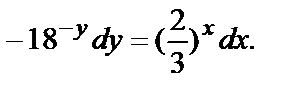 Интегрируя, получим общий интеграл
Интегрируя, получим общий интеграл 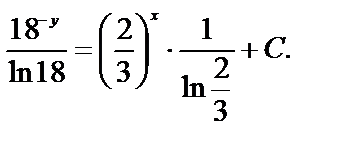
Найдём частное решение Д.У..
№6. 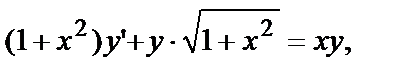 удовлетворяющее начальному условию
удовлетворяющее начальному условию 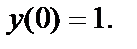
Перенесём второе слагаемое в правую часть, вынесем за скобку множитель y и получим
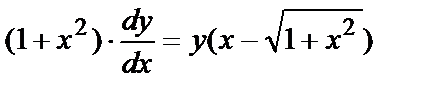 - Д.У. с разделяющимися переменными, для чего умножим на дробь
- Д.У. с разделяющимися переменными, для чего умножим на дробь 

Рассмотрим вначале нужный нам интеграл 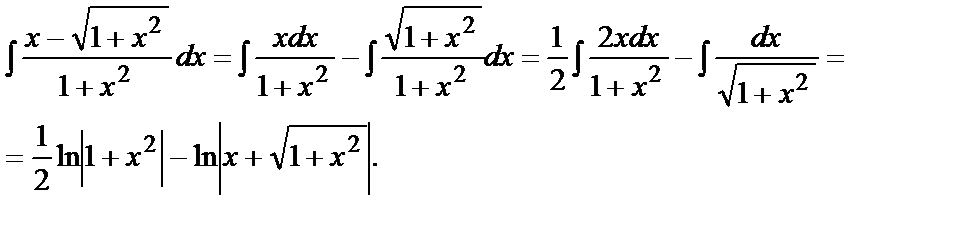
Общий интеграл данного Д.У.:

Используя известные свойства логарифмов, упростим форму общего интеграла 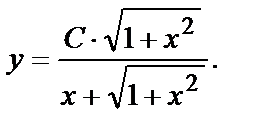
Подставив начальное условие: х=0, у=1, найдём значение постоянной С:
 С=1.
С=1.
Искомый частный интеграл 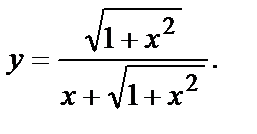
Проверка: 
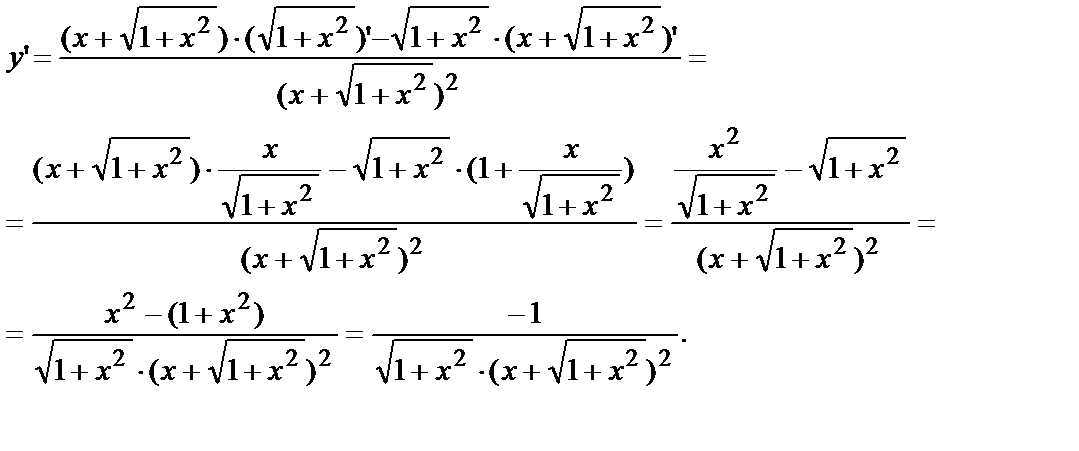
Подставим  и
и 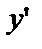 в данное Д.У.:
в данное Д.У.:

Упрощая, получим:

Получено верное равенство, что доказывает, что решение было получено правильно.
Дата добавления: 2015-01-05; просмотров: 263; Мы поможем в написании вашей работы!; Нарушение авторских прав |