
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бесконечные ряды
Приведем слова виднейшего нашего математика А.Я. Хинчина:
«Среди различных математических аппаратов, могущих служить орудиями исследований функций, первое место по простоте, гибкости, прозрачности и удобству употребления, без сомнения, занимают функциональные ряды».
Начнем рассмотрение с бесконечных числовых рядов.
Определение: Бесконечным числовым рядом называется выражение
 где
где 
числовая последовательность.
Числа  называют членами ряда,
называют членами ряда,  - общий член ряда. Иногда числовой ряд записывают с помощью символа суммирования å (сигма).
- общий член ряда. Иногда числовой ряд записывают с помощью символа суммирования å (сигма).

Рассмотрим суммы
 — n-ая частичная сумма ряда.
— n-ая частичная сумма ряда.
Рассмотрим последовательность  частичных сумм ряда и вычислим ее предел (если он существует):
частичных сумм ряда и вычислим ее предел (если он существует): 
Определение.Числовой ряд
 (1)
(1)
называется сходящимся, если существует предел его
частичных сумм  В этом случае предел
В этом случае предел 
называют суммой ряда и записывают 
Если же не существует 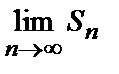 , то ряд называют расходящимся. В частности, если
, то ряд называют расходящимся. В частности, если  , ряд расходится.
, ряд расходится.
Рассмотрим примеры.
Пример 1. Для бесконечного числового ряда
1-1+1-1+1-1+...
найдем частичные суммы:
 .
.
Последовательность частичных сумм 1,0,1,0,1,... не имеет предела следовательно, ряд 1-1+1-1+1-1+... расходится.
Пример 2.Рассмотрим ряд
 .
.
Найдем его частичные суммы, преобразовав вначале дробь 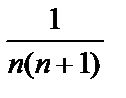 в разность:
в разность: 
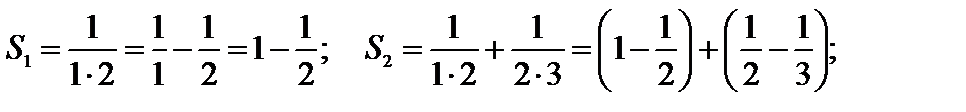
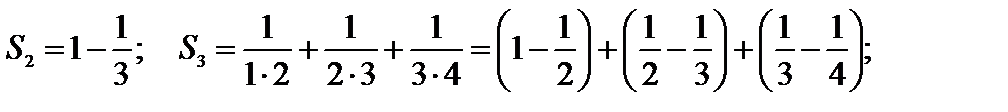

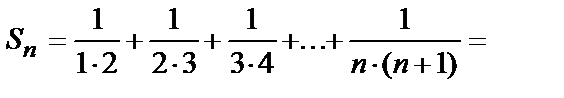

Найдем предел последовательности  частичных сумм:
частичных сумм: 
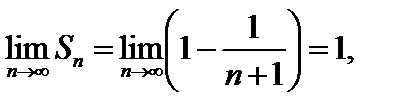 т.к.
т.к.  .
.
Следовательно, ряд сходится и
 .
.
Пример 3. Рассмотрим ряд геометрической прогрессии

Здесь  - первый член,
- первый член,  - знаменатель прогрессии.
- знаменатель прогрессии.
Сумма  членов прогрессии определяется по формуле
членов прогрессии определяется по формуле 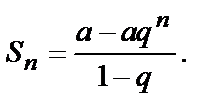
Преобразуем  таким образом:
таким образом:  и рассмотрим три случая:
и рассмотрим три случая:
1)  Тогда
Тогда  неограниченно уменьшаясь стремится к нулю
неограниченно уменьшаясь стремится к нулю
и существует 
2)  Тогда
Тогда  неограниченно возрастает при возрастании
неограниченно возрастает при возрастании 
и не существует 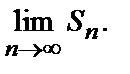
3) Если  , т.е.
, т.е.  то ряд геометрической прогрессии имеет вид:
то ряд геометрической прогрессии имеет вид:
при 
 расходится
расходится
при 
 расходится.
расходится.
Итак,ряд геометрической прогрессии
a + aq + aq2 + aq3 +…+ aqn–1 +…
сходится при  и сумма этого ряда
и сумма этого ряда  .
.
При 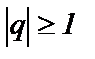 ряд геометрической прогрессии расходится.
ряд геометрической прогрессии расходится.
Например, ряд 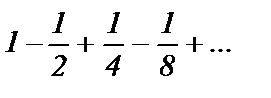 сходится, т. к.
сходится, т. к.  и его сумма
и его сумма
 .
.
Ряд 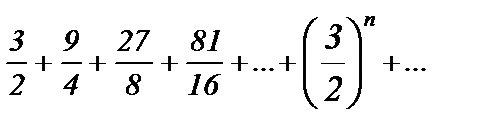 расходится, т. к.
расходится, т. к. 
Докажем теорему о необходимом условии сходимости ряда.
Теорема: Если ряд  сходится, то
сходится, то
 т. е.
т. е.
предел его общего члена стремится к нулю.
Действительно,  . А так как ряд сходится, то существует
. А так как ряд сходится, то существует 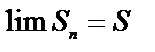 . Но тогда и
. Но тогда и 
Понятно, что  что и требовалось доказать.
что и требовалось доказать.
Замечание. Если необходимый признак сходимости ряда не выполняется, т. е. если  то ряд сходиться не может, ряд расходится.
то ряд сходиться не может, ряд расходится.
Например, числовой ряд

расходится, т. к. его общий член
 и
и  .
.
Условие  является необходимым условием сходимости, оно не является достаточным для сходимости, т. е. если
является необходимым условием сходимости, оно не является достаточным для сходимости, т. е. если  , то ряд может расходиться.
, то ряд может расходиться.
В качестве такого ряда приведем так называемый гармонический ряд:
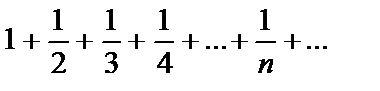
Его общий член  и
и  , но гармонический ряд расходится. Доказательство этого мы дадим позже.
, но гармонический ряд расходится. Доказательство этого мы дадим позже.
Интуитивно понятны и следующие рассуждения.
Рассмотрим ряд

Пусть k – любое натуральное число. Ряд  называется остатком ряда
называется остатком ряда  . Он получается отбрасыванием первых k его членов.
. Он получается отбрасыванием первых k его членов.
Справедлива теорема: Ряд и его остаток одновременно сходятся или расходятся.
Например, ряд геометрической прогрессии
 сходится,
сходится,
т. к.  , и его сумма
, и его сумма

Тогда сходится и ряд  т. к. он является остатком ряда
т. к. он является остатком ряда 
 , но его сумма равна
, но его сумма равна 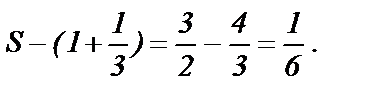
Из суммы первоначального ряда вычитаются отброшенные члены 1 и  . Проверим, что сумма найдена верно. Остаток ряда
. Проверим, что сумма найдена верно. Остаток ряда 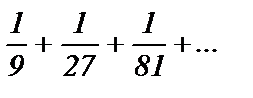 тоже является рядом геометрической прогрессии с тем же знаменателем
тоже является рядом геометрической прогрессии с тем же знаменателем  и первым членом
и первым членом  . По формуле суммы
. По формуле суммы 
Мы можем утверждать, что ряд  расходится, т. к. он является остатком расходящегося гармонического ряда
расходится, т. к. он является остатком расходящегося гармонического ряда  .
.
Ранее мы доказали сходимость ряда
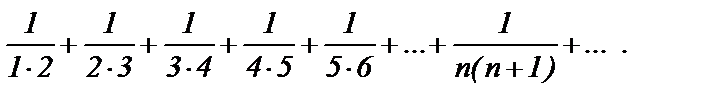
Тогда сходится, например, ряд

 .
.
Дата добавления: 2015-01-05; просмотров: 340; Мы поможем в написании вашей работы!; Нарушение авторских прав |