
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Признак Лейбница.
Если в знакочередующемся ряде
 (все
(все  )
)
члены таковы, что
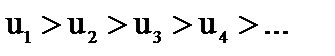 и
и 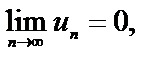 то данный знакочередующийся ряд сходится.
то данный знакочередующийся ряд сходится.
Пример 1. Знакочередующийся ряд
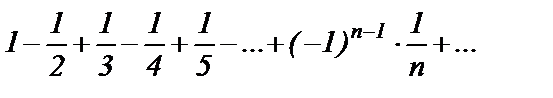 сходится по признаку Лейбница, т.к.
сходится по признаку Лейбница, т.к.
 и
и 
Пример 2. Так же просто убедимся, что знакочередующийся ряд 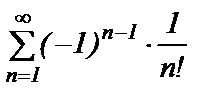 сходится.
сходится.
1) 
и 
2) 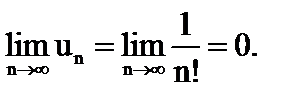
При доказательстве признака Лейбница устанавливается тот факт, что сумма сходящегося знакочередующегося ряда есть положительное число и не превосходит первого члена, т.е. 
Это позволяет дать простую оценку ошибки, которую мы совершаем, заменяя сумму  ряда его частичной суммой
ряда его частичной суммой 
Действительно, если ряд  сходится и его сумма
сходится и его сумма 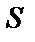 нам неизвестна, то можно положить приближенно, что сумма
нам неизвестна, то можно положить приближенно, что сумма  равна частичной сумме
равна частичной сумме  Но тогда остаток ряда
Но тогда остаток ряда  тоже представляет собой сходящийся знакочередующийся ряд, а его сумма не превосходит
тоже представляет собой сходящийся знакочередующийся ряд, а его сумма не превосходит 
Иначе говоря, если мы полагаем сумму  ряда равной
ряда равной  , то ошибка не превосходит первого отброшенного члена
, то ошибка не превосходит первого отброшенного члена 
Пример 3. Мы уже убедились, что ряд
 сходится.
сходится.
Оценим сумму  этого ряда.
этого ряда.
Если в качестве приближенного значения суммы  мы возьмем
мы возьмем  то ошибка приближения будет меньше или равна
то ошибка приближения будет меньше или равна 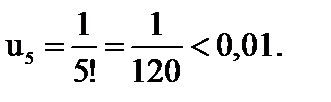 Вычислим
Вычислим 

Итак, полагая 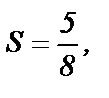 мы сделали ошибку, не превосходящую 0,01. Улучшить точность мы можем, если увеличим число
мы сделали ошибку, не превосходящую 0,01. Улучшить точность мы можем, если увеличим число  членов ряда для подсчета частичной суммы
членов ряда для подсчета частичной суммы 
Дата добавления: 2015-01-05; просмотров: 338; Мы поможем в написании вашей работы!; Нарушение авторских прав |