
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегральный признак Коши.
Пусть члены ряда  положительны и не возрастают, т.е.
положительны и не возрастают, т.е.  и пусть
и пусть  - такая непрерывная возрастающая функция, что при
- такая непрерывная возрастающая функция, что при 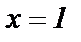
 при
при  при
при  Тогда данный ряд
Тогда данный ряд 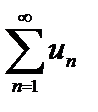 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл  Если же несобственный интеграл
Если же несобственный интеграл  расходится, то расходится и данный ряд.
расходится, то расходится и данный ряд.
С помощью интегрального признака Коши мы легко докажем расходимость гармонического ряда.
Пример 8. Для гармонического ряда


рассмотрим 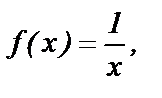 т.к. при
т.к. при 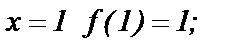 при
при  при
при 
Несобственный интеграл

Т.к. несобственный интеграл расходится, то расходится гармонический ряд 
Пример 9. Исследовать сходимость ряда



Т.к. 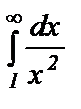 сходится, то сходится ряд
сходится, то сходится ряд 
Пример 10. Исследовать сходимость ряда


Интеграл расходится, значит, расходится ряд 
Вообще, с помощью интегрального признака Коши можно исследовать сходимость ряда общего типа:


при  (расходится)
(расходится)
при  при
при  т.к.
т.к.  и
и 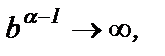 (ряд сходится).
(ряд сходится).
Вывод:
| сходится при а >1 расходится при а ≤ 1 |
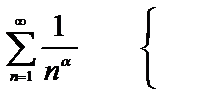
Были рассмотрены достаточные признаки сходимости рядов с положительными членами. Выбрать наиболее подходящий признак для исследования сходимости конкретного ряда можно, имея достаточный опыт.
Отметим некоторые свойства сходящихся рядов.
1. Если даны два сходящихся ряда
 и
и
 (Здесь
(Здесь 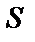 и
и  - суммы данных рядов),
- суммы данных рядов),
то сходятся ряды 
 и
и

Иначе говоря, два сходящихся ряда можно почленно складывать (вычитать).
2. Если ряд  сходится, т.е.
сходится, т.е.  то сходится ряд
то сходится ряд

Обратите внимание: свойства указывают, как находится сумма вновь полученного ряда.
Пример 11. Даны два ряда 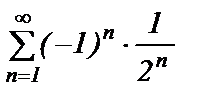 и
и 
Исследуем сходимость этих рядов:

 т.е. сумма первого ряда
т.е. сумма первого ряда 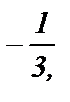 сумма второго ряда 1. Оба ряда – ряды геометрической прогрессии — сходятся и суммы их найдены по формуле
сумма второго ряда 1. Оба ряда – ряды геометрической прогрессии — сходятся и суммы их найдены по формуле 
Складывая почленно, получим

Получен ряд геометрической прогрессии с первым членом  и
и
знаменателем 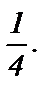 По формуле его сумма
По формуле его сумма 
Действительно, пользуясь свойством, складывая суммы данных рядов, получим 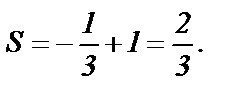
Рассмотренный пример демонстрирует справедливость свойства 1.
Рассмотрим ряды, члены которых имеют различные знаки. Начнем с так называемых знакочередующих рядов.
Дата добавления: 2015-01-05; просмотров: 316; Мы поможем в написании вашей работы!; Нарушение авторских прав |