
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение. Сходящийся знакопеременный ряд называется абсолютно
сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
В рассмотренном примере ряд  является абсолютно сходящимся.
является абсолютно сходящимся.
Определение. Сходящийся знакопеременный ряд называется условно
сходящимся, если ряд, составленный из абсолютных величин его членов, расходится.
Например, ряд 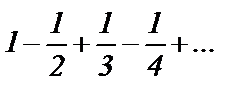 сходится по признаку Лейбница, а ряд из абсолютных величин расходится как гармонический
сходится по признаку Лейбница, а ряд из абсолютных величин расходится как гармонический  .
.
Итак, ряд  условно сходится.
условно сходится.
Между свойствами абсолютно и условно сходящихся рядов имеется глубокое различие.
В абсолютно сходящемся ряде можно переставлять местами члены ряда, т.е. в результате перестановки членов получим ряд, сумма которого не меняется.
В условно сходящемся ряде от перестановки членов ряда меняется его сумма. Более того, в условно сходящемся ряде можно так переставить члены, что полученный ряд окажется расходящимся.
Пример 2. Пусть  сумма условно сходящегося ряда
сумма условно сходящегося ряда

Переставим его члены так, чтобы после одного положительного члена шло два отрицательных. Получим ряд:

Мы получили исходный ряд, умноженный на  , сумма его также уменьшена вдвое. Получили мы этот факт только в результате перестановки членов ряда.
, сумма его также уменьшена вдвое. Получили мы этот факт только в результате перестановки членов ряда.
В этом же ряде
 (5)
(5)
переставим его члены иначе.
Для начала запишем ряд (5) в виде
 (6)
(6)
В ряде (6) первый член оказался на втором месте, второй – на четвертом и т.д. Умножим равенство (6) на 
 (7)
(7)
Сложим почленно два сходящихся ряда (5) и (7), получим новый ряд
 (8)
(8)
Ряд (8) получен из ряда (5) перестановкой его членов: второй член оказался на третьем месте, третий – на втором, четвертый – на шестом и т.д. , а сумма ряда (8) уже равна 
Таким образом, из одного и того же условно сходящегося ряда с суммой  различными перестановками его членов мы получили ряд с суммой
различными перестановками его членов мы получили ряд с суммой 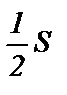 и другой ряд с суммой
и другой ряд с суммой 
Этот вывод, который на первый взгляд кажется парадоксальным, говорит о том, что бесконечные ряды отличаются по своим свойствам от сумм конечного числа слагаемых.
Еще в ХVIII веке математики часто упускали из виду это обстоятельство и приходили к неверным результатам. Строгая теория бесконечных рядов была разработана в ХIХ веке после того, как весь математический анализ был перестроен на базе теории пределов.
Дата добавления: 2015-01-05; просмотров: 287; Мы поможем в написании вашей работы!; Нарушение авторских прав |