
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Степенные ряды
Специальный класс функциональных рядов составляют так называемые степенные ряды, т.е. ряды вида

где  действительные числа. Степенные ряды построены как обобщение понятия многочлена. Они имеют наиболее простую структуру, и их свойства значительно проще, чем свойства произвольных функциональных рядов. Приведем без доказательства наиболее важные теоремы о степенных рядах.
действительные числа. Степенные ряды построены как обобщение понятия многочлена. Они имеют наиболее простую структуру, и их свойства значительно проще, чем свойства произвольных функциональных рядов. Приведем без доказательства наиболее важные теоремы о степенных рядах.
Теорема 1. Областью сходимости всякого степенного ряда является интервал с центром в начале координат.
Заметим, что степенный ряд может сходиться только в одной точке  (пример 7 п. 6.8); возможно также, что степенный ряд сходится на интервале
(пример 7 п. 6.8); возможно также, что степенный ряд сходится на интервале  т.е. при любом
т.е. при любом  (пример 8 п.6.8). Во всех остальных случаях существует такое число R>0, что степенной ряд сходится в интервале (-R,R) и расходится вне этого интервала, т.е. при
(пример 8 п.6.8). Во всех остальных случаях существует такое число R>0, что степенной ряд сходится в интервале (-R,R) и расходится вне этого интервала, т.е. при  и
и 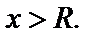 В точках
В точках  и
и  степенной ряд может как сходиться, так и расходиться. Ряд, рассмотренный в примере 1 п. 6.8, сходиться на интервале (-1,1), т.е. для всех
степенной ряд может как сходиться, так и расходиться. Ряд, рассмотренный в примере 1 п. 6.8, сходиться на интервале (-1,1), т.е. для всех  удовлетворяющих неравенству
удовлетворяющих неравенству 
Ряд в примере 3 п. 6.8 сходится на интервале  т.е. для всех
т.е. для всех  удовлетворяющих неравенству
удовлетворяющих неравенству 
Ряд в примере 6 п. 6.8 сходится для  .
.
Теорема 2. Внутри интервала сходимости степенной ряд можно почленно дифференцировать.
Следовательно, если степенной ряд сходится на интервале  и
и  его сумма, т.е. для
его сумма, т.е. для 

то при  выполняется равенство
выполняется равенство

Пример 1. Воспользуемся полученным в примере 1 п. 6.8 равенством
 для
для 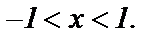
Продифференцируем обе части этого равенства для любого указанного 
Для 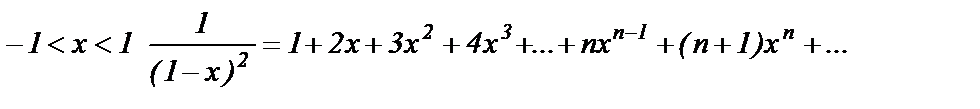
Мы получили разложение в степенной ряд функции  имея разложение для функции
имея разложение для функции 
Теорема 3. Степенной ряд можно почленно интегрировать на любом отрезке внутри интервала сходимости.
Это значит, что при  из равенства
из равенства
 для
для  следует равенство
следует равенство

Пример 2. Имеем  для
для 
Интегрируя на  , получим
, получим

Пусть  где
где 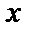 любое число из указанного интервала (-1,1).
любое число из указанного интервала (-1,1).

Для любого  из (-1,1) мы получили
из (-1,1) мы получили 
Т.к. в (-1,1) для любого 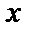 существует ему противоположное число -
существует ему противоположное число -  заменим в последнем равенстве
заменим в последнем равенстве  на
на 


Умножив на –1 обе части, получим

С помощью полученного равенства – разложения в ряд функции  - можно составить таблицу значений логарифма натурального с любой нужной нам степенью точности. Например, при
- можно составить таблицу значений логарифма натурального с любой нужной нам степенью точности. Например, при 

Если ограничиться четырьмя первыми слагаемыми, то  мы вычислим с точностью до 0,01, т.к.
мы вычислим с точностью до 0,01, т.к.  0,01.
0,01.
Действительно, мы получим  т.е. с точностью до
т.е. с точностью до  (сравните:
(сравните:  в четырехзначных таблицах).
в четырехзначных таблицах).
Пример 3.Функциональный ряд  сходится как ряд геометрической прогрессии со знаменателем
сходится как ряд геометрической прогрессии со знаменателем  для
для  (или
(или  , и его суммой является функция
, и его суммой является функция  .
.
 для
для 
Проинтегрируем полученное равенство для  из указанной области сходимости
из указанной области сходимости

Для  из (-1,1)
из (-1,1) 
мы получили разложение в ряд функции 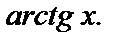
Дата добавления: 2015-01-05; просмотров: 334; Мы поможем в написании вашей работы!; Нарушение авторских прав |