
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Образец выполнения контрольного задания
Задача № 3. Среди данных последовательностей выделить арифметическую или геометрическую последовательности и для каждой из них написать формулу для суммы  первых
первых  членов.
членов.
а)  эта последовательность не является ни арифметической, ни геометрической.
эта последовательность не является ни арифметической, ни геометрической.
б)  эта последовательность является геометрической, т.к. каждый ее член получен умножением предыдущего на одно и то же число
эта последовательность является геометрической, т.к. каждый ее член получен умножением предыдущего на одно и то же число  Первый член ее
Первый член ее  знаменатель
знаменатель 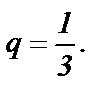 Формула общего члена:
Формула общего члена:
 Формула суммы
Формула суммы  первых
первых  членов:
членов:

в) 1, 4, 7, 10, 13, … - арифметическая последовательность с первым членом  и разностью
и разностью 

г) 49, 42, 35, 28, … — арифметическая прогрессия:

Задача № 4. Написать пять первых членов ряда и проверить, выполняется ли необходимый признак сходимости.
a) 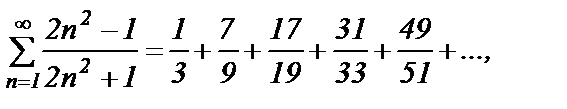
т.к. 
Найдем 
(мы разделили числитель и знаменатель на  и учли, что
и учли, что  при
при  ). Т.к. необходимый признак сходимости не выполняется, то ряд расходится.
). Т.к. необходимый признак сходимости не выполняется, то ряд расходится.
б) 
 не существует, т.к. при неограниченном увеличении аргумента
не существует, т.к. при неограниченном увеличении аргумента  синус его меняется от –1 до 1 и от 1 до –1 и не стремится ни к какому пределу.
синус его меняется от –1 до 1 и от 1 до –1 и не стремится ни к какому пределу.
Т.к.  то ряд расходится.
то ряд расходится.
Задача № 5. Исследовать сходимость ряда
а) 
Данный знакоположительный ряд сравним с рядом геометрической прогрессии  со знаменателем
со знаменателем  который сходится.
который сходится.
Т.к.  то ряд
то ряд  сходится
сходится
б)  . Исследуем этот знакоположительный ряд по признаку Даламбера.
. Исследуем этот знакоположительный ряд по признаку Даламбера. 
Вычислим 
ряд расходится.
в)  Рассмотрим вначале ряд
Рассмотрим вначале ряд  и исследуем его по интегральному признаку Коши. В качестве функции
и исследуем его по интегральному признаку Коши. В качестве функции  выберем положительную функцию
выберем положительную функцию 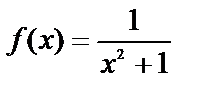 , для которой при
, для которой при  при
при 
при 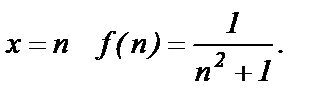
Вычислим несобственный интеграл

Т.к. несобственный интеграл сходится, то сходится ряд 
Сравним с ним данный ряд 
Т.к.  то данный ряд сходится.
то данный ряд сходится.
Задача № 6. Выяснить, какой из данных рядов сходится абсолютно, какой
сходится условно, какой расходится.
а)  знакочередующийся ряд, который представляет собой частный случай знакопеременного ряда. Исследуем ряд из абсолютных величин
знакочередующийся ряд, который представляет собой частный случай знакопеременного ряда. Исследуем ряд из абсолютных величин  по признаку Даламбера.
по признаку Даламбера.

Т.к. ряд из абсолютных величин сходится, то данный ряд
 сходится абсолютно.
сходится абсолютно.
б)  знакочередующийся ряд. По признаку Лейбница сравним абсолютные величины членов ряда:
знакочередующийся ряд. По признаку Лейбница сравним абсолютные величины членов ряда:
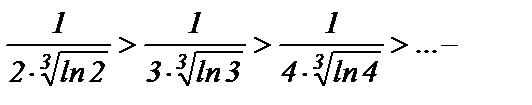 убывают. И предел общего члена
убывают. И предел общего члена  . По признаку Лейбница ряд сходится.
. По признаку Лейбница ряд сходится.
Чтобы выяснить, как сходится этот ряд, исследуем ряд из абсолютных величин  по интегральному признаку.
по интегральному признаку.
Выберем функцию  определенную на множестве
определенную на множестве  .
.
Несобственный интеграл

 расходится, тогда и ряд из абсолютных величин расходится. Поэтому данный ряд
расходится, тогда и ряд из абсолютных величин расходится. Поэтому данный ряд  сходится условно.
сходится условно.
в)  Для этого знакочередующегося ряда не выполняется условие
Для этого знакочередующегося ряда не выполняется условие 
Действительно,  Ряд расходится.
Ряд расходится.
Задача № 7. Найти область сходимости ряда 
Для любого  степенной ряд
степенной ряд
 является
является
знакопеременным рядом.
Рассмотрим ряд из абсолютных величин его членов и применим признак Даламбера




По признаку Даламбера для сходимости ряда требуется  Это значит, степенной ряд сходится при
Это значит, степенной ряд сходится при  Мы получили интервал сходимости (-1,1) данного ряда
Мы получили интервал сходимости (-1,1) данного ряда  Остается выяснить, как ведет себя ряд на концах этого интервала.
Остается выяснить, как ведет себя ряд на концах этого интервала.
Пусть  Получим
Получим  знакочередующийся ряд. По признаку Лейбница он сходится, т.к.
знакочередующийся ряд. По признаку Лейбница он сходится, т.к.
 убывают и
убывают и
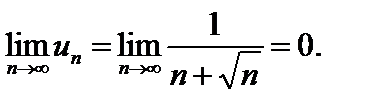
Поэтому  входит в область сходимости ряда.
входит в область сходимости ряда.
Пусть  Получим
Получим 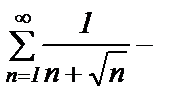 знакоположительный ряд. Общий член этого ряда
знакоположительный ряд. Общий член этого ряда  не меньше общего члена ряда
не меньше общего члена ряда  расходится, как гармонический ряд, умноженный почленно на
расходится, как гармонический ряд, умноженный почленно на 
Итак, область сходимости степенного ряда  , т.е. ряд сходится для
, т.е. ряд сходится для 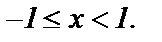
Задача № 8. Вычислить значение функции с указанной точностью,
использовав ряд Тейлора для этой функции.
С точностью 0,0001 вычислить 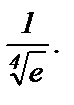 Число
Число  можно рассматривать как значение функции
можно рассматривать как значение функции  при
при  Ряд Тейлора для нее:
Ряд Тейлора для нее:

При  получим
получим

В полученном знакочередующемся ряде точность вычисления оценивается по первому отброшенному члену:
 что и требовалось.
что и требовалось.
Итак,  с точностью до 0,00001.
с точностью до 0,00001.
Задача № 9. Вычислить  с указанной точностью.
с указанной точностью.
Вычислить  с точностью до 0,001.
с точностью до 0,001.
Можно воспользоваться полученным в примере № 3 § 9 разложением функции  в ряд Тейлора. Покажем еще раз, как можно получить разложение в ряд Тейлора интеграла
в ряд Тейлора. Покажем еще раз, как можно получить разложение в ряд Тейлора интеграла 
1. Запишем ряд геометрической прогрессии
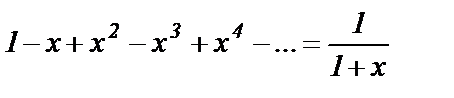 для
для 
Здесь 
 .
.
2. Подставим в этот ряд  вместо
вместо  Получим разложение для функции
Получим разложение для функции
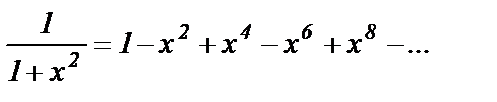 для
для 
3. Проинтегрируем последний ряд на интервале  где
где 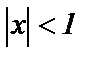
 или
или
 для
для 
4. Разделим обе части полученного равенства на 
а при  вспомним, что
вспомним, что 
 для
для 
5. Наконец, проинтегрировав на  , получим для
, получим для 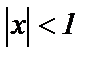
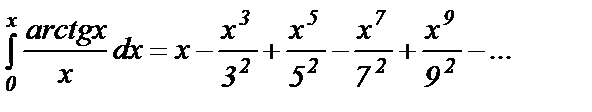
6. При  =
=
=  с точностью до 0,001, т.к.
с точностью до 0,001, т.к.


Дата добавления: 2015-01-05; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав |