
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Производная по направлению. Градиент
Пусть функция  определена в некоторой области, включающей точку М(х,у). Перейдём из точки М(х,у) в точку М1(х1,у1), перемещаясь по заданному направлению
определена в некоторой области, включающей точку М(х,у). Перейдём из точки М(х,у) в точку М1(х1,у1), перемещаясь по заданному направлению  Будем считать, что вектор
Будем считать, что вектор  образует с осями координат Ох и Оу углы a и b
образует с осями координат Ох и Оу углы a и b  тогда вектор смещения
тогда вектор смещения  ММ1 совпадает с вектором
ММ1 совпадает с вектором  Функция
Функция  получит при этом полное приращение
получит при этом полное приращение  Отношение
Отношение  полного приращения функции к длине вектора смещения равно средней скорости изменения функции.
полного приращения функции к длине вектора смещения равно средней скорости изменения функции.
Определение. Предел отношения  при стремлении точки M1 к точке М, если он существует и конечен, называется производной функции
при стремлении точки M1 к точке М, если он существует и конечен, называется производной функции  в точке М(х,у) по направлению вектора
в точке М(х,у) по направлению вектора 
Обозначают производную по направлению  Так как отношение
Так как отношение  равно средней скорости изменения функции
равно средней скорости изменения функции  на участке ММ1, то его предел при
на участке ММ1, то его предел при  естественно принять за истинную скорость изменения функции z в точке М в направлении вектора
естественно принять за истинную скорость изменения функции z в точке М в направлении вектора  Таков физический смысл производной по направлению.
Таков физический смысл производной по направлению.
Если функция  дифференцируема в точке М(х,у), то её полное приращение в этой точке
дифференцируема в точке М(х,у), то её полное приращение в этой точке

|
 Обозначим
Обозначим 
 - длина вектора ММ1,
- длина вектора ММ1, 
 - приращения независимых переменных. Очевидно, что
- приращения независимых переменных. Очевидно, что 
 и при
и при  , т.е.
, т.е. 
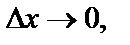


Запишем полное приращение в виде
 тогда
тогда  где
где  и
и  - бесконечно малые при
- бесконечно малые при 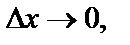
 Переходя к пределу при
Переходя к пределу при  получили
получили  и
и 
Формула для производной по направлению принимает вид:
 Легко видеть, что если направление
Легко видеть, что если направление  совпадает с направлением оси Ох, то
совпадает с направлением оси Ох, то 
 и производная по направлению оси Ох совпадает с частной производной по переменной х:
и производная по направлению оси Ох совпадает с частной производной по переменной х: 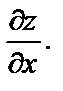 Аналогично, производная по направлению оси Оу совпадает с частной производной
Аналогично, производная по направлению оси Оу совпадает с частной производной  Таким образом, частные производные по переменным х и у являются частным случаем более общего понятия производной по направлению.
Таким образом, частные производные по переменным х и у являются частным случаем более общего понятия производной по направлению.
Если рассмотреть функцию трёх переменных  и направление
и направление  образующее с осями координат
образующее с осями координат  углы
углы  соответственно, то производная функции u в точке М(x,y,z) вычисляется по формуле
соответственно, то производная функции u в точке М(x,y,z) вычисляется по формуле
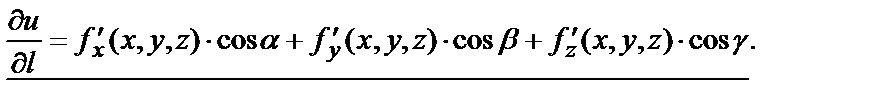
Рассмотрим примеры.
№ 1. Вычислить производную функции  в точке А(1,2) по направлению вектора
в точке А(1,2) по направлению вектора  где точка В(4,-2).
где точка В(4,-2).
Так как формула производной по направлению  то найдём
то найдём  и
и  - координаты единичного вектора направления
- координаты единичного вектора направления 
 Его координаты найдём, зная координаты конца В(4,-2) и начала А(1,2) этого вектора:
Его координаты найдём, зная координаты конца В(4,-2) и начала А(1,2) этого вектора:  Длина вектора
Длина вектора  Тогда
Тогда 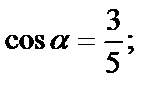

Найдём частные производные данной функции  и
и  и вычислим их значение в точке А(1,2).
и вычислим их значение в точке А(1,2). 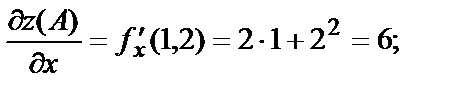
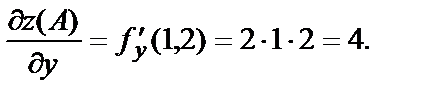 Искомая производная по направлению в точке А(1,2) имеет значение:
Искомая производная по направлению в точке А(1,2) имеет значение:

№ 2. Найти производную функции  по направлению вектора
по направлению вектора  в точках
в точках  и
и 
Запишем формулу для производной функции трёх переменных по направлению 
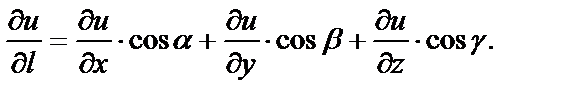
Найдём направляющие косинусы 

 вектора
вектора  или координаты его единичного вектора. Для этого разделим координаты вектора
или координаты его единичного вектора. Для этого разделим координаты вектора  на его длину
на его длину 
Получим 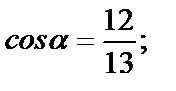

 Найдём частные производные данной функции
Найдём частные производные данной функции 

В любой точке М(x,y,z) формула производной по направлению  имеет вид:
имеет вид: 
Подставляя координаты точек А(0,-2,-1) и В(3,3,5), получим значения производной по направлению:


Рассмотрим далее очень важное для приложений понятие градиента функции.
Определение. Вектор с координатами  и
и  вычисленными в точке М(x,y), называется градиентом функции
вычисленными в точке М(x,y), называется градиентом функции 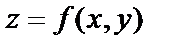 в этой точке и обозначается grad z или grad f(x,y).
в этой точке и обозначается grad z или grad f(x,y).
По определению этот вектор  или
или  где
где 
 - базисные векторы координатных осей Ох и Оу соответственно. Напомним, что любой вектор
- базисные векторы координатных осей Ох и Оу соответственно. Напомним, что любой вектор  плоскости можно разложить по базисным векторам
плоскости можно разложить по базисным векторам 
 зная координаты
зная координаты 
 этого вектора:
этого вектора: 
И если даны два вектора  и
и  то их скалярное произведение
то их скалярное произведение 
Формула производной по направлению  где
где  и
и  - направляющие косинусы направления
- направляющие косинусы направления 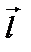 или координаты его единичного вектора. Обозначив через
или координаты его единичного вектора. Обозначив через  этот единичный вектор
этот единичный вектор  запишем его разложение по базису
запишем его разложение по базису 


Градиент функции z в точке (х,у) 
Вычислим скалярное произведение этих двух векторов  Производная по направлению в точке равна скалярному произведению градиента в этой точке и единичного вектора этого направления.
Производная по направлению в точке равна скалярному произведению градиента в этой точке и единичного вектора этого направления.
А так как по определению скалярного произведения  то
то  поскольку
поскольку  Здесь
Здесь  - угол между направлением
- угол между направлением 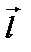 и градиентом. Принимая во внимание, что самое большое значение косинуса
и градиентом. Принимая во внимание, что самое большое значение косинуса  при
при  можно утверждать, что производная по направлению
можно утверждать, что производная по направлению  будет наибольшей, когда направление
будет наибольшей, когда направление  совпадает с направлением градиента. Итак, доказано важное физическое толкование полученного свойства:
совпадает с направлением градиента. Итак, доказано важное физическое толкование полученного свойства:
градиент функции в точке указывает направление наибольшей скорости изменения функции в этой точке.
Легко видеть, что эта наибольшая скорость изменения функции  равна модулю градиента (ведь
равна модулю градиента (ведь  ).
).
Обобщим понятие градиента для функции  трёх переменных:
трёх переменных:
 Здесь
Здесь 

 - базис в пространстве, частные производные функции
- базис в пространстве, частные производные функции 

 должны быть вычислены в точке М(x,y,z).
должны быть вычислены в точке М(x,y,z).
№ 3. Найти и построить градиент функции  в точке A(-1,0).
в точке A(-1,0).

|

 и вычислим их значения в точке A(-1,0).
и вычислим их значения в точке A(-1,0).
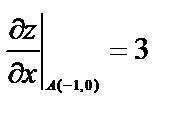 ;
; 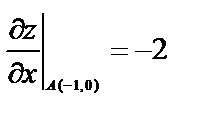
Искомый вектор 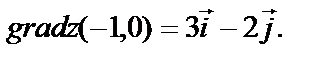
Построим его в данной точке A(-1,0).
Рассмотрим геометрическую задачу с использованием дифференциального исчисления функции двух переменных. Это задача о составлении уравнения касательной плоскости к поверхности. Прежде всего – понятие касательной плоскости.
Пусть дана поверхность уравнением  где функция
где функция 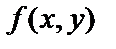 дифференцируема в точке М0(х0,у0). Будем называть касательной плоскостью к поверхности в точке Р плоскость, которая имеет с поверхностью единственную общую точку, а именно – точку Р.
дифференцируема в точке М0(х0,у0). Будем называть касательной плоскостью к поверхности в точке Р плоскость, которая имеет с поверхностью единственную общую точку, а именно – точку Р.

|
 и
и  А так как точка Р лежит на поверхности с уравнением
А так как точка Р лежит на поверхности с уравнением  то для неё третья координата
то для неё третья координата  где
где 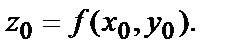
Уравнение касательной плоскости к поверхности  в точке
в точке  имеет вид:
имеет вид:
 .
.
Сравним уравнение касательной плоскости к поверхности с уравнением касательной к плоской линии  в точке, где
в точке, где  Это уравнение рассматривается и в курсе средней школы, и в курсе высшей математики (часть № 3) и имеет вид:
Это уравнение рассматривается и в курсе средней школы, и в курсе высшей математики (часть № 3) и имеет вид:
 где
где 
Аналогия очевидна. В случае функции двух переменных, при помощи которой задано уравнение поверхности, уравнение касательной плоскости содержит похожие слагаемые, которых теперь два: это произведение значения частной производной на разность между х и х0 (или между у и у0).
Рассмотрим пример № 4.
Составить уравнение касательной плоскости к поверхности 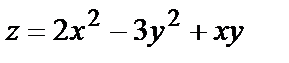 в точке, где
в точке, где 

Найдём 



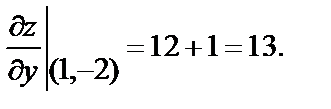
Подставим полученные значения в уравнение

Уравнение искомой касательной плоскости:
 или
или

Пример № 5. К поверхности 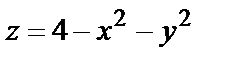 провести касательную плоскость, параллельную плоскости
провести касательную плоскость, параллельную плоскости 
В этом случае нам не даны координаты точки касания, поэтому используем условие параллельности двух плоскостей (часть 2).
Пусть  и
и

уравнения двух параллельных плоскостей. Тогда их нормальные векторы 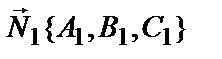 и
и  тоже параллельны, то есть
тоже параллельны, то есть  - условие параллельности плоскости. В нашем примере дана плоскость уравнением
- условие параллельности плоскости. В нашем примере дана плоскость уравнением  Вторая плоскость – касательная плоскость с уравнением
Вторая плоскость – касательная плоскость с уравнением  или
или

Условие их параллельности 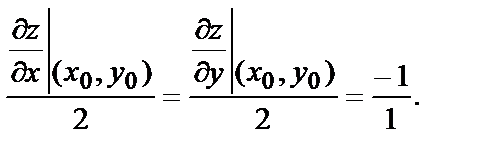
Отсюда 

Т.к. уравнение поверхности  то
то 

 и
и  Получим
Получим 
 Из уравнения поверхности
Из уравнения поверхности 
Искомое уравнение  или
или
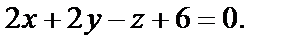
Дата добавления: 2015-01-05; просмотров: 538; Мы поможем в написании вашей работы!; Нарушение авторских прав |