
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Как выполнить экзаменационное задание
Экзаменационное задание предполагает использование большинства разделов, изложенных в темах 1 - 7 учебно-методических материалов, а именно:
решение систем уравнений;
вектор, направляющие косинусы, длина вектора, угол между векторами, операции над векторами;
уравнение прямой на плоскости;
построение графика функции;
кривые второго порядка и их уравнения;
уравнение плоскости в пространстве;
формулы и правила дифференцирования функции одной переменной;
исследование на экстремум;
дифференциальное исчисление функции двух переменных, приложения.
Все эти вопросы можно найти в любом стандартном учебнике по математическому анализу и линейной алгебре для студентов вузов. Список нужной литературы прилагается в темах 1 - 7 учебно-методических материалов.
В экзаменационном задании предлагается функция двух переменных 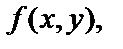 для которой нужно провести исследование на экстремум, найти наибольшее и наименьшее её значения в замкнутой области, решить несколько прикладных геометрических и физических задач. Каждая конкретная задача проанализирована и подробно решена в тексте (номер примера и номер параграфа указан). Тем не менее, ниже приведён пример выполнения одного экзаменационного задания.
для которой нужно провести исследование на экстремум, найти наибольшее и наименьшее её значения в замкнутой области, решить несколько прикладных геометрических и физических задач. Каждая конкретная задача проанализирована и подробно решена в тексте (номер примера и номер параграфа указан). Тем не менее, ниже приведён пример выполнения одного экзаменационного задания.
1. Исследовать на экстремум функцию 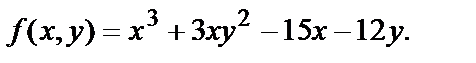
Данная функция  определена при всех
определена при всех  и
и 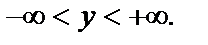
Найдём критические точки функции, для чего используем необходимые условия существования экстремума:
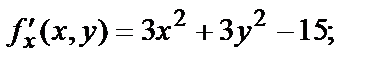
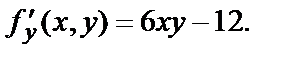
Решим систему:  или
или 
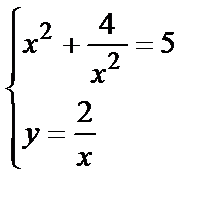

Из первого уравнения: 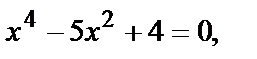 или
или  и
и 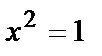 имеем четыре корня
имеем четыре корня 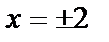 и
и 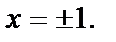 Принимая во внимание второе уравнение системы
Принимая во внимание второе уравнение системы 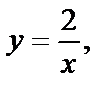 получим Р1(2,1), Р2(-2,-1), Р3(1,2), Р4(-1,-2) — четыре критические точки.
получим Р1(2,1), Р2(-2,-1), Р3(1,2), Р4(-1,-2) — четыре критические точки.
Чтобы установить, в какой из них существует экстремум, используем достаточные условия. Составим выражение  и вычислим его в каждой критической точке.
и вычислим его в каждой критической точке.

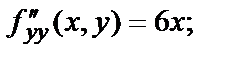

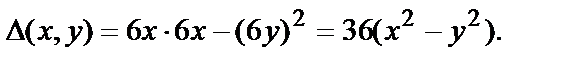
Вычислим значение 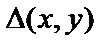 в каждой точке.
в каждой точке. 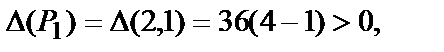 т.е. в точке Р1(2,1) есть экстремум, а т.к.
т.е. в точке Р1(2,1) есть экстремум, а т.к. 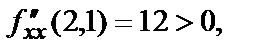 то точка Р1(2,1) – точка минимума.
то точка Р1(2,1) – точка минимума.
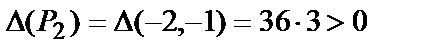 и
и  точка Р2(-2,-1) – точка максимума.
точка Р2(-2,-1) – точка максимума.
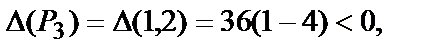 т.е. в точке Р3(1,2) – нет экстремума.
т.е. в точке Р3(1,2) – нет экстремума.
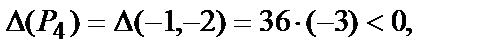 т.е. в точке Р4(-1,-2) нет экстремума.
т.е. в точке Р4(-1,-2) нет экстремума.
Остаётся вычислить минимальное и максимальное значения функции:

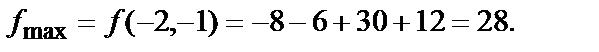
2. Найти наибольшее и наименьшее значения функции  в области, которая представляет собой четырёхугольник с вершинами О(0,0), А(3,1), С(3,3), В (0,-2).
в области, которая представляет собой четырёхугольник с вершинами О(0,0), А(3,1), С(3,3), В (0,-2).
Построим данные точки и составим уравнения сторон четырёхугольника.

|
Прямая АС имеет уравнение: х=3.
Прямая ОС имеет уравнение: у=х.
Уравнение прямой АВ получим как уравнение прямой, проходящей через две точки (х1,у1) и (х2,у2).
 Пусть
Пусть 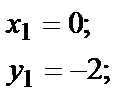
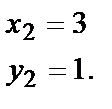
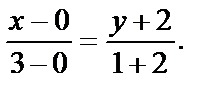 Отсюда
Отсюда 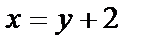 или
или 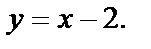
Ранее были получены четыре критических точки этой функции: Р1(2,1), Р2(-2,-1), Р3(1,2), Р4(-1,-2), из которых только одна точка Р1(2,1) принадлежит данной области. (Кстати, ОВАС - параллелограмм). Значение функции в точке Р1 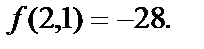 Остальные не интересуют.
Остальные не интересуют.
Найдём наибольшее и наименьшее значения функции  на границе данной области, которая состоит из четырёх отрезков разных прямых.
на границе данной области, которая состоит из четырёх отрезков разных прямых.
На ОС: у=х. Подставим в данную функцию выражение для у (у=х) и получим функцию только одной переменной х. Обозначим её 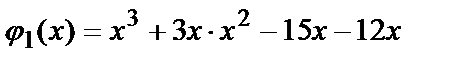 или
или 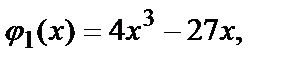 где
где 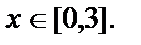
Найдём её производную и приравняем её к нулю: 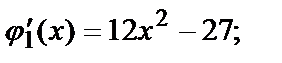
 Получим две критические точки
Получим две критические точки  и
и  из которых только
из которых только  принадлежит отрезку [0,3]. Так как у=х, то
принадлежит отрезку [0,3]. Так как у=х, то 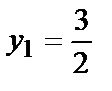 и мы получим точку
и мы получим точку  значение в которой
значение в которой 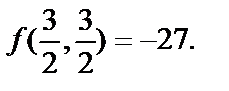 Значения функции
Значения функции 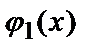 на концах отрезка [0,3] и значения данной функции в точках (0,0) и (3,3) попарно совпадают, т.е.
на концах отрезка [0,3] и значения данной функции в точках (0,0) и (3,3) попарно совпадают, т.е.
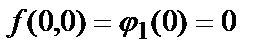

На АС: х=3. Подставим в функцию  х=3, получим функцию одной переменной у.
х=3, получим функцию одной переменной у.
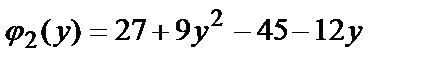 или
или
 где
где 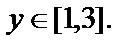

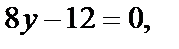
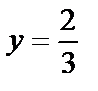 не принадлежит
не принадлежит  поэтому рассмотрим значения
поэтому рассмотрим значения 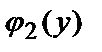 в точках
в точках 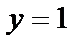 и
и 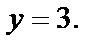 А так как
А так как 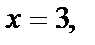 то для данной функции
то для данной функции  получим значения в точках
получим значения в точках 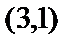 и
и 

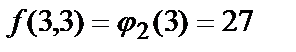 (это значение уже было вычислено).
(это значение уже было вычислено).
На АВ: 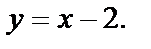 Подставив в функцию
Подставив в функцию 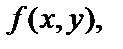 получим
получим 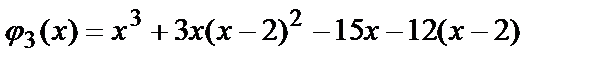 или
или
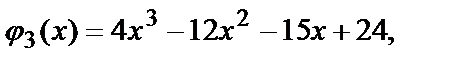 где
где 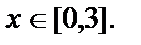
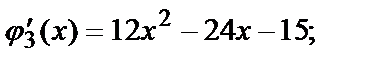
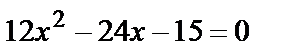 или
или 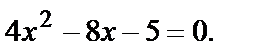 Решим квадратное уравнение:
Решим квадратное уравнение: 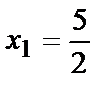 и
и 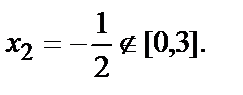
Вычислим значение функции 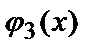 в точке
в точке  Так как
Так как  то
то 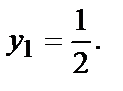
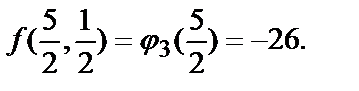
Значения на концах отрезка  и
и 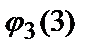 совпадают со значениями функции
совпадают со значениями функции  в точках (0,-2) и (3,1).
в точках (0,-2) и (3,1).
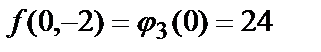
 (уже были получены).
(уже были получены).
На ОВ: 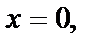 получили функцию
получили функцию
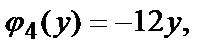 где
где 
 Не может быть
Не может быть  т.е. критических точек нет. Значения на концах отрезка уже получены.
т.е. критических точек нет. Значения на концах отрезка уже получены.
Среди значений функции  получены: -28; -27; 0; 27; -21; -26; 24.
получены: -28; -27; 0; 27; -21; -26; 24.
Наименьшее значение функция 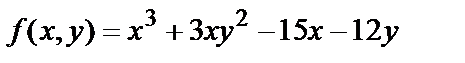 в параллелограмме ОСАВ имеет в точке Р1(2,1):
в параллелограмме ОСАВ имеет в точке Р1(2,1):

Наибольшее значение эта функция имеет в точке С(3,3):
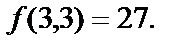
3. Составить уравнение касательной плоскости к поверхности  в точке, где
в точке, где 
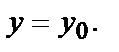
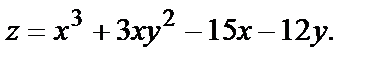
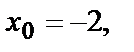

Вычислим 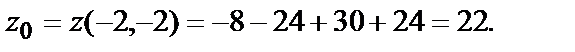
Частные производные функции  и
и 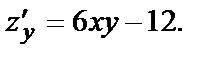
Их значения в точке (-2,-2):

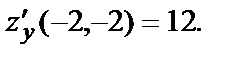
Уравнение касательной плоскости:

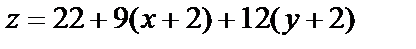 или
или
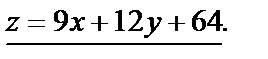
4. Найти наибольшую скорость возрастания функции 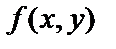 в точке М1(0,2).
в точке М1(0,2).
Наибольшая скорость возрастания функции в точке равна модулю градиента её.
Найдём 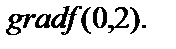
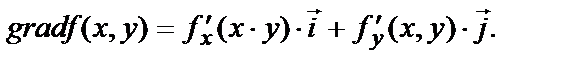


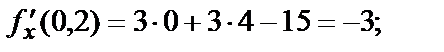
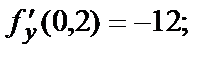
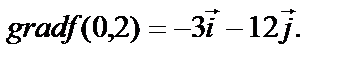
Модуль этого вектора равен
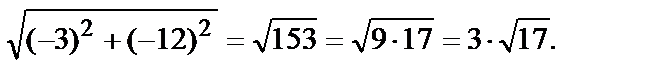
Таким образом, наибольшая скорость возрастания функции  в точке М1(0,2) равна
в точке М1(0,2) равна 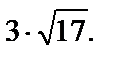
5. Вычислить производную функции 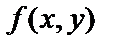 в точке М1(0,2) в направлении вектора
в точке М1(0,2) в направлении вектора 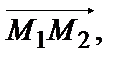 где точка М2(1,1). Каков характер изменения функции в точке М1?
где точка М2(1,1). Каков характер изменения функции в точке М1?
Формула производной по направлению 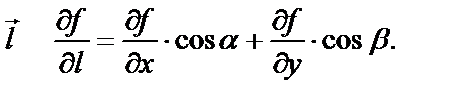
Направление 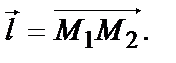 По координатам точек М1(0,2) и М2(1,1) найдём координаты вектора
По координатам точек М1(0,2) и М2(1,1) найдём координаты вектора 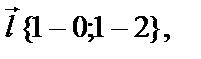 т.е.
т.е. 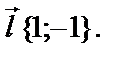 Длина этого вектора равна
Длина этого вектора равна  Разделив вектор
Разделив вектор 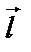 на его длину
на его длину 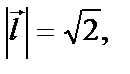 получим
получим 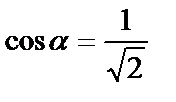 и
и 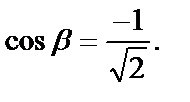 Вычислим значения
Вычислим значения 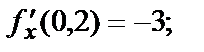
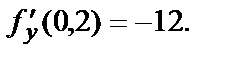 Подставим в формулу производной по направлению:
Подставим в формулу производной по направлению:
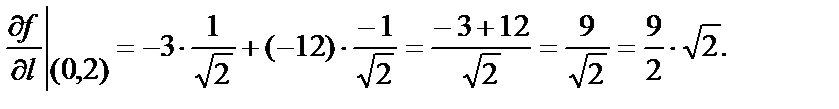
Так как 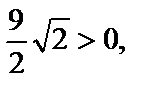 то скорость функции положительна, т.е. функция
то скорость функции положительна, т.е. функция 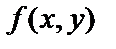 в точке М1(0,2) по направлению вектора
в точке М1(0,2) по направлению вектора 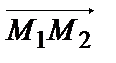 возрастает. Ранее была найдена наибольшая скорость функции, равная
возрастает. Ранее была найдена наибольшая скорость функции, равная 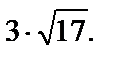
Действительно, 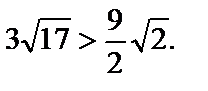
6. Найти угол между градиентами функции 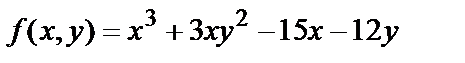 в точках М1(0,2) и М2(1,1).
в точках М1(0,2) и М2(1,1).
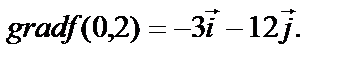
Найдём градиент в точке М2(1,1).
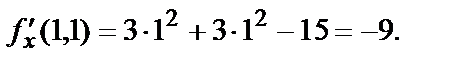


Угол между векторами  и
и 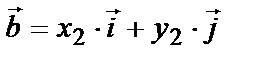 найдём по формуле
найдём по формуле 
В нашем случае

Искомый угол 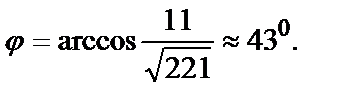

Дата добавления: 2015-01-05; просмотров: 261; Мы поможем в написании вашей работы!; Нарушение авторских прав |