
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Наибольшее и наименьшее значения функции
Понятия наибольшего и наименьшего значений функции двух переменных определяются так же, как и для функции одной переменной.
Наибольшее или наименьшее из всех значений функции нельзя смешивать с максимумом и минимумом функции.
Если функция  определена и непрерывна в замкнутой ограниченной области D, то она принимает в этой области свои наибольшее и наименьшее значения.
определена и непрерывна в замкнутой ограниченной области D, то она принимает в этой области свои наибольшее и наименьшее значения.
Пусть  и
и  - такие точки, что
- такие точки, что  - наибольшее значение,
- наибольшее значение,  - наименьшее значение. Заметим, что таких точек может быть несколько. Тогда для всех точек
- наименьшее значение. Заметим, что таких точек может быть несколько. Тогда для всех точек 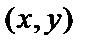 области D:
области D:
 и
и 
Если точка  (или точка
(или точка  ) лежит внутри области D, то это точка максимума (или минимума) функции
) лежит внутри области D, то это точка максимума (или минимума) функции  т.е.
т.е.  и
и  - критические точки функции внутри области D.
- критические точки функции внутри области D.
Поэтому при решении задачи отыскания наибольшего и наименьшего значений функции в области нужно найти те критические её точки, которые лежат внутри области, вычислить значения функции в них, а затем исследовать значения функции на границе области.
Чтобы найти наибольшее и наименьшее значения функции  в области D, можно руководствоваться следующим правилом:
в области D, можно руководствоваться следующим правилом:
1) Найти критические точки функции, решив систему 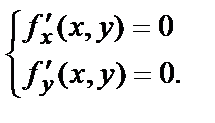
2) Не проводя исследования на экстремум, вычислить значение функции  только в тех критических точках, которые лежат в области.
только в тех критических точках, которые лежат в области.
3) Найти наибольшее (наименьшее) значение функции на границе области, для чего нужно знать уравнение этой границы и воспользоваться соответствующим правилом для функции одной переменной.
4) Из всех полученных значений функции выбрать самое большое (наибольшее значение) и самое маленькое (наименьшее значение).
Напомним, как решалась задача об отыскании наибольшего и наименьшего значений функции одной переменной на отрезке.
Правило для нахождения наибольшего и наименьшего значений функции 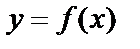 на отрезке
на отрезке 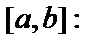
1) Найти критические точки функции  решив уравнение
решив уравнение 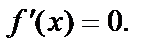
2) Вычислить значение функции  в каждой критической точке, лежащей внутри отрезка
в каждой критической точке, лежащей внутри отрезка 
3) Вычислить значения функции  на концах отрезка, т.е.
на концах отрезка, т.е. 
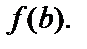
4) Из полученных значений функции выбрать самое большое и самое маленькое.
Пример № 1. Найти наибольшее и наименьшее значения функции
 на отрезке
на отрезке 
Найдём критические точки, решив уравнение 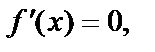 т.е.
т.е. 

 - две критические точки, из которых
- две критические точки, из которых  не входит в данный отрезок
не входит в данный отрезок  Поэтому вычислим значение данной функции
Поэтому вычислим значение данной функции  только в точке
только в точке 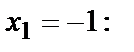
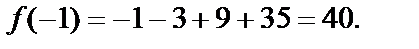
Вычислим значения  на концах отрезка:
на концах отрезка: 

Получены три значения: 40, -41, 13.
Наибольшее значение функции  на отрезке
на отрезке 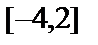 равно 40 и достигается ею в критической точке
равно 40 и достигается ею в критической точке 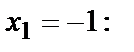

Наименьшее значение функции  равно –41 и достигается в граничной точке
равно –41 и достигается в граничной точке 

Такие задачи потребуется решать при рассмотрении поведения функции двух переменных  на границе области D.
на границе области D.
Рассмотрим несколько примеров основной задачи этого параграфа.
Решение каждой такой задачи довольно громоздко, требует внимания и аккуратности оформления.
Пример № 2. Найти наибольшее и наименьшее значения функции

 в треугольнике с вершинами О(0,0), А(6,0), В(0,6).
в треугольнике с вершинами О(0,0), А(6,0), В(0,6).
Построим треугольник ОАВ и запишем уравнения прямых, на которых лежат стороны треугольника.
Уравнение прямой АВ получим как уравнение прямой, проходящей через две данные точки:
 где
где 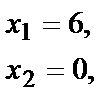

Уравнение АВ: 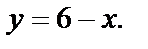
Найдём критические точки функции

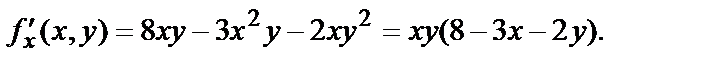
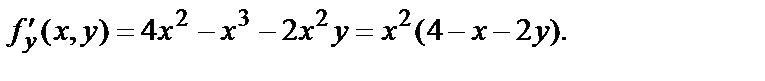
Для решения системы 
рассмотрим все возможные случаи: 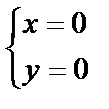


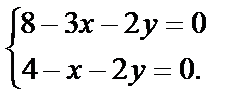
Первые три критические точки: О(0,0), М1(4,0), М2(0,4) получены из первых трёх простейших систем. Найдём координаты четвёртой, решив систему:
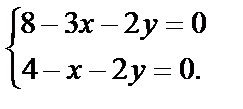
Вычитая из первого уравнения второе, получим  Тогда
Тогда  Итак, М3(2,1).
Итак, М3(2,1).
Вычислим значение данной функции  в полученных точках, так как все они находятся в пределах данного треугольника ОАВ:
в полученных точках, так как все они находятся в пределах данного треугольника ОАВ:


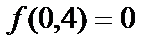
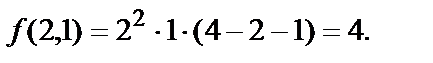
Найдём наибольшее и наименьшее значения функции  на границе данной области, которая состоит из трёх отрезков прямых: АВ, ОА, ОВ.
на границе данной области, которая состоит из трёх отрезков прямых: АВ, ОА, ОВ.
На отрезке ОА  поэтому данная функция
поэтому данная функция  принимает в каждой точке ОА постоянное значение
принимает в каждой точке ОА постоянное значение  На отрезке ОВ
На отрезке ОВ  поэтому
поэтому  На отрезке АВ
На отрезке АВ  подставим в данную функцию
подставим в данную функцию 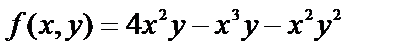 выражение
выражение  и получим функцию одной переменной х, которую обозначим
и получим функцию одной переменной х, которую обозначим

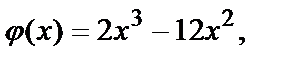 где
где 
Найдём критические точки этой функции на отрезке 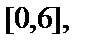 решив уравнение
решив уравнение 


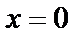 и
и  - критические точки принадлежат
- критические точки принадлежат 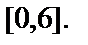
Найдём 
Так как на отрезке АВ  , то
, то
при 
 получим точку (0,6);
получим точку (0,6);
при 
 получим точку (4,2);
получим точку (4,2);
при 
 получим точку (6,0).
получим точку (6,0).
Таким образом, для данной функции двух переменных  получили значения:
получили значения:
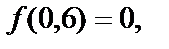


Среди различных значений функции  получены числа: 0; 4; -64.
получены числа: 0; 4; -64.
Наибольшее значение функции равно 4 – значения функции в точке (2,1), 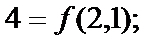
наименьшее значение функции равно –64, это значение функции в точке (4,2)

Пример № 3. Найти наибольшее и наименьшее значение функции 

|




Составим уравнение прямых
АВ:  или
или 
ВС: 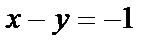 или
или 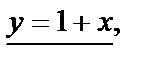
СЕ:  или
или 
ЕА:  или
или 
Найдём критические точки функции из системы 


Полученная критическая точка (6,-8) не принадлежит данной области и поэтому рассматривать её не будем.
Граница данной области состоит из четырёх отрезков:
1) на АВ  Подставив выражение для y в данную функцию
Подставив выражение для y в данную функцию  получим функцию одной переменной х:
получим функцию одной переменной х:
 или
или
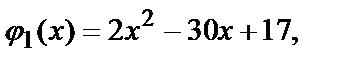 где
где 
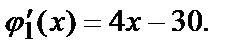
 ;
; 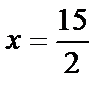 не принадлежит [0,1].
не принадлежит [0,1].
Остаётся рассмотреть  и
и 
Тогда соответствующие значения переменной  равны
равны  и
и 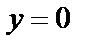 . Получили две точки (0,1) и (1,0), значения в которых для исходной функции
. Получили две точки (0,1) и (1,0), значения в которых для исходной функции 


2) На ВС  Подставив у в функцию
Подставив у в функцию  получим функцию одной переменной х:
получим функцию одной переменной х:
 или
или
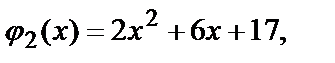 где
где 

 ;
; 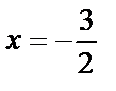 не принадлежит [-1,0].
не принадлежит [-1,0].
При 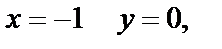 при
при 
Вычислим значения функции  в полученных точках (-1,0) и (0,1)
в полученных точках (-1,0) и (0,1)


3) На СЕ 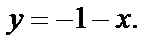 Подставив в
Подставив в  получим:
получим:
 или
или
 где
где 
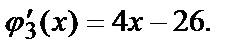
 ;
; 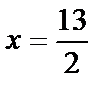 не принадлежит [-1,0].
не принадлежит [-1,0].
При  при
при 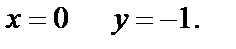
Вычислим значения функции  в полученных точках (-1,0) и (0,-1)
в полученных точках (-1,0) и (0,-1)


4) На ЕА  Подставив в
Подставив в  получим:
получим:
 или
или
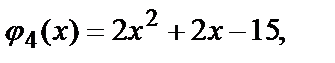 где
где 

 ;
;  не принадлежит [0,1].
не принадлежит [0,1].
При 
 , при
, при 


Среди различных значений функции  получены числа 17; -11; 13;
получены числа 17; -11; 13;
-15.
Наибольшее значение функции равно 17, наименьшее значение равно –15.


Пример № 4. Найти наибольшее и наименьшее значения функции

в замкнутой области D, ограниченный линиями  и
и 
Найдём критические точки функции:

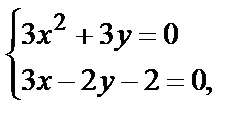


|
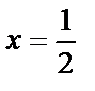 и
и 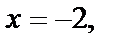 а из первого уравнения соответствующие значения
а из первого уравнения соответствующие значения  и
и  Таким образом, мы получили две
Таким образом, мы получили две
критические
точки 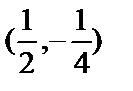 и
и  .Построим заданную область:
.Построим заданную область:  - парабола и
- парабола и  - прямая.
- прямая.
Точка (-2,-4) не принадлежит области D, её рассматривать не будем.
Вычислим значения

Граница области D состоит из двух кусков различных кривых: из дуги параболы  и отрезка прямой
и отрезка прямой  .
.
1) На прямой АВ 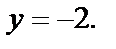 Подставим это значение у в данную функцию
Подставим это значение у в данную функцию  Получим функцию одной переменной х:
Получим функцию одной переменной х:
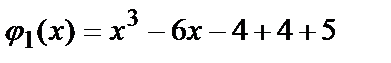 или
или
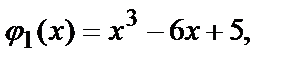 где
где 

 ,
, 
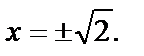
Получим две точки 

Вычислим значение функции  в этих точках и на концах отрезка в AB точках А(2,-2) и В(-2,-2).
в этих точках и на концах отрезка в AB точках А(2,-2) и В(-2,-2).




2) На дуге параболы  Подставим y в
Подставим y в 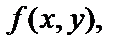 получим:
получим:
 или
или
 где
где 
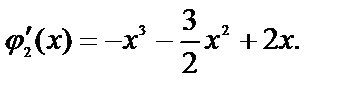
Решим уравнение:  или
или



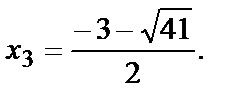
Т.к.  то
то  не принадлежит отрезку [-2,2]. Вычислим значение функции при
не принадлежит отрезку [-2,2]. Вычислим значение функции при 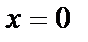 и при
и при 
При 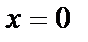 у=0 и
у=0 и 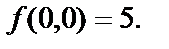
При  найдём значение
найдём значение 
 это и будет значение функции
это и будет значение функции  в точке
в точке 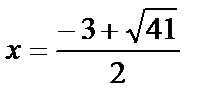 при
при 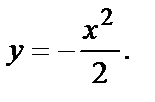
Среди различных значений функции  мы получили числа:
мы получили числа:
1; 5; 9; 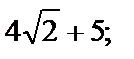



Учитывая, что 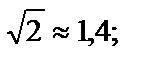
 отмечаем, что наибольшее из них равно
отмечаем, что наибольшее из них равно 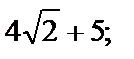 наименьшее равно
наименьшее равно 


Вопросы для самоконтроля
1. Дайте определение функции двух переменных.
2. Какова геометрическая интерпретация функции двух переменных?
3. Что называется областью определения функции двух переменных?
4. Каково геометрическое изображение функции двух переменных?
5. Дайте определение предела функции двух переменных в точке?
6. Какая функция  называется непрерывной в точке М0(х0,у0)?
называется непрерывной в точке М0(х0,у0)?
7. Что называют частным приращением функции  в точке, полным приращением в точке?
в точке, полным приращением в точке?
8. Дайте определение частной производной функции  по переменной х (по переменной у).
по переменной х (по переменной у).
9. Как вычислить значение в точке частной производной а) по х, б) по у?
10. Каков геометрический смысл частной производной по х в данной точке?
11. Дайте определение производной по направлению от функции 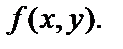
12. Какова формула для вычисления производной по направлению?
13. Что называется градиентом функции  в данной точке? Чем геометрически изображается градиент?
в данной точке? Чем геометрически изображается градиент?
14. Какова связь между градиентом и производной по направлению?
15. Каков физический смысл градиента и производной по направлению?
16. Как найти величину наибольшей скорости изменения функции в точке?
17. Что называется касательной плоскостью к поверхности? Как записать уравнение касательной плоскости к поверхности в данной точке?
18. Что называют частной производной второго (третьего) порядка для функции нескольких переменных?
19. Сколько различных частных производных второго порядка для функции  вы можете назвать? Как они обозначаются и как находятся?
вы можете назвать? Как они обозначаются и как находятся?
20. Какое значение функции  называется максимальным (минимальным)?
называется максимальным (минимальным)?
21. Дать определение точки максимума (минимума) для функции  Каково приращение функции в точке максимума (минимума)?
Каково приращение функции в точке максимума (минимума)?
22. Что называют экстремумом функции? точкой экстремума функции  ?
?
23. Каковы необходимые условия существования экстремума?
24. Что называют критической точкой функции? Всегда ли критическая точка является точкой экстремума?
25. Каковы достаточные условия существования экстремума?
26. Каково правило отыскания наибольшего и наименьшего значений функции в области?
Если вы испытываете трудности при ответе на предложенные вопросы, обратитесь вновь к настоящему курсу. Ответы на поставленные вопросы вы найдёте в указанных пунктах.
В п. 7.1 – вопросы с 1 по 6.
В п. 7.2 – вопросы с 7 по 10.
В п. 7.3 – вопросы с 11 по 17.
В п. 7.4 – вопросы 18 и 19.
В п. 7.5 – вопросы с 20 по 25.
В п. 7.6 – вопрос 26.
Дата добавления: 2015-01-05; просмотров: 1091; Мы поможем в написании вашей работы!; Нарушение авторских прав |