Ряд Тейлора

Аппарат степенных рядов играет в математическом анализе и в приложениях чрезвычайно важную роль. Рассмотрим возможность представления функции в виде степенного ряда.

Пусть степенной ряд сходится в некотором интервале к функции , т.е.

(1)

Покажем, что возможен единственный степенной ряд, сумма которого равна данной функции

Полагая в равенстве (1) получим

Продифференцируем равенство (1):

(2)

Полагая в равенстве (2) получим

или

Продифференцируем равенство (2):

(3)

Полагая в равенстве (3) получим

или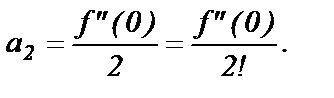

Затем аналогично,

(4)

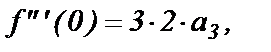или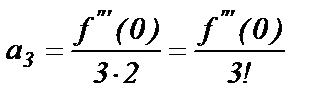

Продолжая этот процесс раз, получим

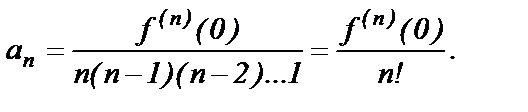
Итак, мы показали, что если функция представлена в виде степенного ряда (1), то его коэффициенты определяются по формулам

и сам ряд имеет вид

(5)

Тем самым мы показали, что не может быть двух степенных рядов, представляющих одну и ту же функцию.

Закономерен вопрос, какой должна быть функция чтобы ее можно было представить степенным рядом (5). Понятно, что для должны существовать ее производные любого порядка в точке Например, для функции 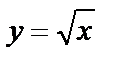ряд (5) составить нельзя, т.к. не существует.

Закономерен также вопрос и об области сходимости ряда (5) к данной функции. Может оказаться, что ряд (5) сходится не во всей области определения функции Например, функция при определена, но подсчитать значение этой функции с помощью ряда

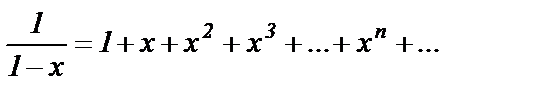при 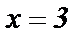нельзя, т.к. этот ряд сходится только при

Определение. Рядом Тейлора для функции называется ряд

(5)

Ряд Тейлора можно составить для определения всякой функции если она определена вместе со своими производными любого порядка в окрестности точки

Степенные ряды являются основным инструментом для изучения функций. Поэтому чрезвычайно важно знать, при каких условиях данная функция может быть суммой составленного для нее ряда Тейлора.

Обозначим через 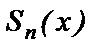частичную сумму ряда (5) и через остаток ряда. Выясним, для каких 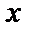суммой ряда (5) будет функция Тогда в этой области

А так как сумма ряда есть то

Таким образом доказана

Теорема: Функция является суммой ряда Тейлора (5) в области, где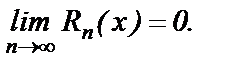

Для остатка 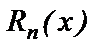справедлива формула, которую примем без доказательства

где с- некоторое число между и

Итак, если определена вместе с производными любого порядка в окрестности точки то в области, где является суммой своего ряда Тейлора, т.е. в этой области

Для определения области сходимости ряда Тейлора к функции требуется найти, для каких

Заметим, что в формуле остатка

есть дробь

Покажем, что для любого действительного числа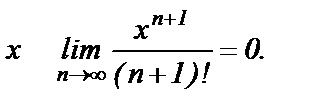

В примере 8 п.6.8 мы показали, что ряд сходится для любого Но тогда для любого 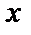выполняется необходимый признак сходимости ряда: или Это равносильно равенству 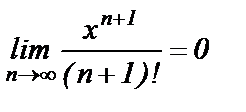для любого Рассмотрим разложение в ряд Тейлора некоторых функций.

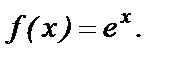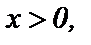Пример 1. Рассмотрим функцию Ее производная любого порядка Поэтому эта функция вместе со всеми своими производными определена для любого Формула для имеет вид где некоторое число между и Будем считать, что тогда и или т.к. функция возрастающая. Так как величина ограниченная, то каково бы ни было действительное число 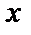А это значит, что область сходимости ряда Тейлора к функции есть интервал Имея в виду, что получим: для всех действительных

Пример 2. Эта функция и ее производные

определены для любого

Все производные четного порядка равны 0, производные нечетного порядка равны 1 или –1 (чередуясь).

Ряд Тейлора для 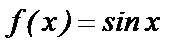имеет вид

Найдем область сходимости этого ряда к функции

рассмотрев остаток

Производная любого порядка функции равна либо либо 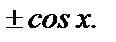В любой точке Поэтому для любого т.к. для любого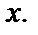

Итак, для всех действительных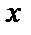

Пример 3. Получим ряд Тейлора для функции для чего достаточно продифференцировать ряд Тейлора для

Итак, для всех действительных

Заметим, что два последних ряда (для и ) подтверждают нечетность функции (ряд содержит только нечетные степени 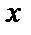) и четность функции (ряд содержит только четные степени ).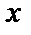

Для простоты изложения был рассмотрен ряд Тейлора в окрестности Для многих функций удобнее пользоваться более общими рядами.

.

Отметим также, что большое приложение имеет разложение функций в тригонометрический ряд Фурье: