
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функциональные ряды
Определение. Функциональным рядом называется ряд
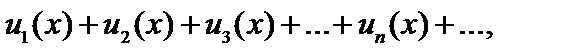 члены которого
члены которого 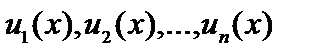 являются функциями от x.
являются функциями от x.
Давая переменной х определенное числовое значение хо, мы получим числовой ряд
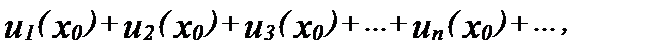
который может быть как сходящимся, так и расходящимся.
Определение.Областью сходимости функционального ряда  называется множество тех значений переменной х, при которых ряд сходится.
называется множество тех значений переменной х, при которых ряд сходится. 
Понятно, что в области сходимости сумма функционального ряда является некоторой функцией от 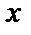 . Обозначим ее через
. Обозначим ее через 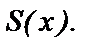

Пример 1. Рассмотрим функциональный ряд
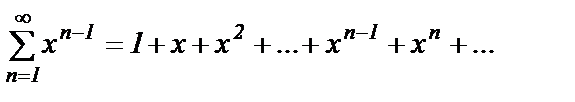
При любом значении 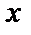 он представляет собой геометрическую прогрессию со знаменателем
он представляет собой геометрическую прогрессию со знаменателем 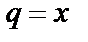 и первым членом 1. Поскольку ряд геометрической прогрессии сходится при
и первым членом 1. Поскольку ряд геометрической прогрессии сходится при  то данный ряд сходится при всех
то данный ряд сходится при всех 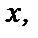 для которых
для которых 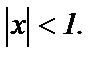 Сумма этого ряда для
Сумма этого ряда для 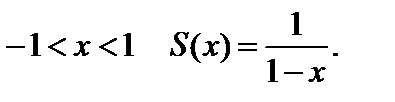
Итак, мы показали, что для всех

При всех других 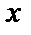 рассмотренный ряд расходится. Областью сходимости функционального ряда
рассмотренный ряд расходится. Областью сходимости функционального ряда 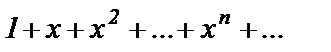 является интервал (-1,1).
является интервал (-1,1).
Пример 2. Рассмотрим функциональный ряд
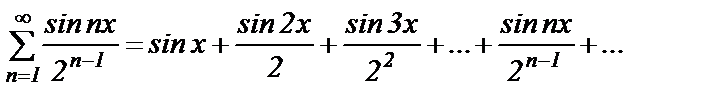
При любом конкретном значении 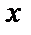 мы получим в общем случае знакопеременный ряд. Для исследования его сходимости рассмотрим ряд из абсолютных величин его членов
мы получим в общем случае знакопеременный ряд. Для исследования его сходимости рассмотрим ряд из абсолютных величин его членов  и сравним его с рядом
и сравним его с рядом
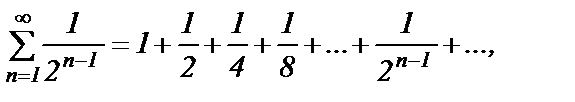 который сходится как ряд геометрической прогрессии со знаменателем
который сходится как ряд геометрической прогрессии со знаменателем 
А т.к. 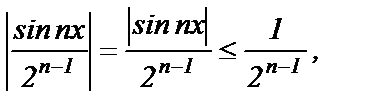 то ряд
то ряд  сходится, но тогда сходится и данный ряд при любом
сходится, но тогда сходится и данный ряд при любом 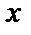 . Следовательно, областью сходимости функционального ряда
. Следовательно, областью сходимости функционального ряда 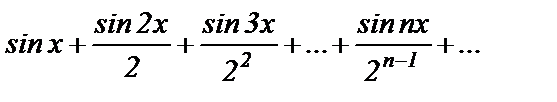 является интервал
является интервал 
Пример 3. Дан функциональный ряд

Найдем область сходимости этого ряда. При постоянном значении 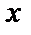 данный ряд может быть знакопеременным. Поэтому рассмотрим ряд из абсолютных величин
данный ряд может быть знакопеременным. Поэтому рассмотрим ряд из абсолютных величин 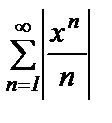 и исследуем его по признаку Даламбера.
и исследуем его по признаку Даламбера. 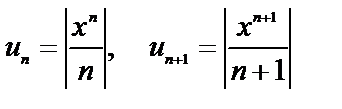 .
.
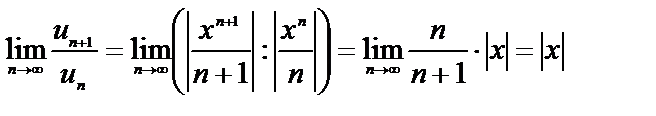
По признаку Даламбера при  ряд сходится, при
ряд сходится, при 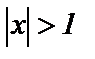 ряд расходится. Поскольку ряд из абсолютных величин сходится при
ряд расходится. Поскольку ряд из абсолютных величин сходится при 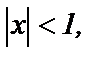 то и ряд
то и ряд  сходится при
сходится при 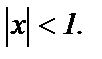 Остается рассмотреть поведение ряда при
Остается рассмотреть поведение ряда при  т.е. при
т.е. при  Это можно сделать непосредственной подстановкой
Это можно сделать непосредственной подстановкой 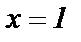 и
и 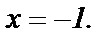
При  получим
получим  знакочередующийся ряд, который сходится по признаку Лейбница.
знакочередующийся ряд, который сходится по признаку Лейбница.
При 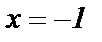 получим
получим 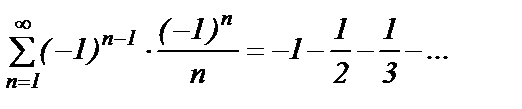 . Этот ряд можно записать в виде
. Этот ряд можно записать в виде 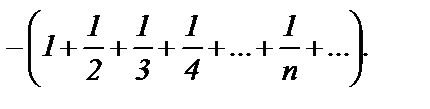 Ясно, что он расходится как гармонический. Итак, областью сходимости ряда
Ясно, что он расходится как гармонический. Итак, областью сходимости ряда  является интервал
является интервал 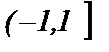 .
.
Пример 4. Найдем область сходимости функционального ряда

составленного из показательных функций. При любом х это ряд с положительными членами вида 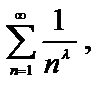 который сходится при
который сходится при 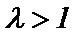 и расходится при
и расходится при 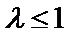 . Поэтому данный ряд
. Поэтому данный ряд 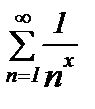 сходится при х>1. Итак, областью сходимости ряда
сходится при х>1. Итак, областью сходимости ряда  является интервал
является интервал 
Пример 5.Члены функционального ряда
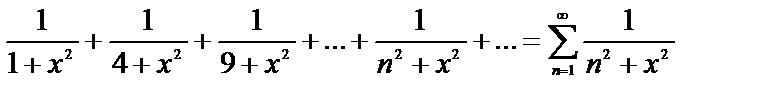
при любом х не больше соответствующих членов сходящегося ряда

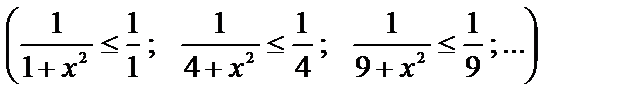 .
.
Поэтому при любом х ряд 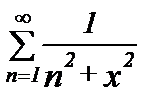 сходится, т. е. областью сходимости ряда
сходится, т. е. областью сходимости ряда  является интервал
является интервал 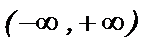 .
.
Пример 6. Функциональный ряд
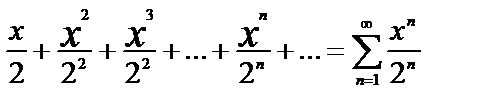
при любом 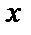 представляет собой ряд геометрической прогрессии со знаменателем
представляет собой ряд геометрической прогрессии со знаменателем  а поэтому сходится при
а поэтому сходится при 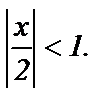
Областью сходимости ряда  является интервал (-2,2).
является интервал (-2,2).
Пример 7. Функциональный ряд 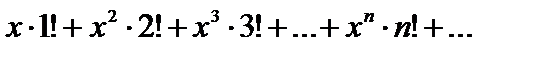
сходится только при 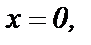 его сумма равна 0 при
его сумма равна 0 при 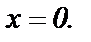
Действительно, применив признак Даламбера к ряду  из абсолютных величин, получим
из абсолютных величин, получим

при любом 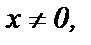 т.е. при любом
т.е. при любом 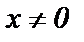 ряд расходится. Областью сходимости ряда
ряд расходится. Областью сходимости ряда  является единственное число
является единственное число 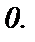
Пример 8. Очень похож на рассмотренный функциональный ряд
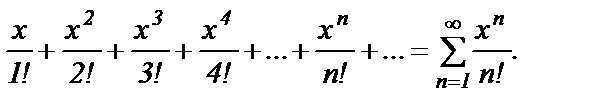
Рассуждая аналогично примеру 7, получим 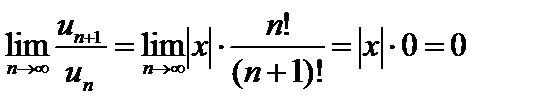
Т.е. ряд 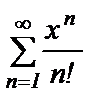 сходится при любом
сходится при любом 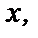 областью его сходимости является интервал
областью его сходимости является интервал 
Дата добавления: 2015-01-05; просмотров: 358; Мы поможем в написании вашей работы!; Нарушение авторских прав |