Лекция 1. МАТЕМАТИЧЕСКИЕ СХЕМЫ МОДЕЛИРОВАНИЯ СИСТЕМ

Модель системы S описывается:

множеством входных воздействий на систему

множеством воздействий внешней среды

множеством внутренних (собственных) параметров системы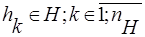

множеством выходных характеристик системы .

В общем случае являются элементами непересекающихся множеств и содержат детерминированные и стохастические составляющие; являются независимыми (экзогенными) переменными, а являются зависимыми (эндогенными) переменными. Процесс функционирования системы S описывается оператором : 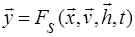- закон функционирования системы; - выходная траектория. задается функцией, алгоритмом, логическими условиями, таблицей, словесным описанием. Алгоритмом функционирования называется метод получения выходных характеристик с учетом . Если , то модель статическая; если , то модель динамическая.

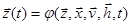Совокупность всех возможных состояний модели системы образует пространство состояний объекта , где ; - свойство системы в конкретный момент времени. Состояние системы в момент времени полностью определяется начальными условиями , входными воздействиями , внутренними параметрами , воздействиями внешней среды с помощью уравнений и .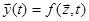

В общем случае время в модели системы рассматривается на интервале моделирования как непрерывное, так и дискретное, квантованное на отрезки длиной , где - число интервалов дискретизации. Этот принцип называется принципом , который является наиболее универсальным принципом, позволяющим определить последовательные состояния процесса функционирования системы через заданные интервалы времени, но с точки зрения затрат машинного времени он иногда оказывается неэкономичным.

Если математическая модель не содержит элементов случайности, или они не учитываются, то есть считается, что стохастические воздействия внешней среды и внутренние параметры отсутствуют, то модель считается детерминированной, тогда . В практике моделирования объектов в области системотехники и системного анализа используются типовые математические схемы, имеющие преимущество простоты и наглядности. Для детерминированных систем в непрерывном времени применяются дифференциальные, интегральные, интегро-дифференциальные уравнения, а в дискретном времени - конечные автоматы и конечно-разностные схемы. Для стохастических моделей с дискретным временем используются вероятностные автоматы, а для стохастических моделей с непрерывным временем - системы массового обслуживания. Для больших информационно-управляющих систем применяются агрегативныемодели, для которых объект или система расчленяется на конечное число частей (подсистем) с сохранением связей, обеспечивающих взаимодействие частей. [18]

Отслеживая при моделировании системы только ее особые состояния в те моменты времени, когда эти состояния имеют место, можно получить информацию, необходимую для построения функций z= 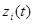по принципу особых состояний (принцип 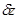),где 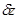- релейное (скачкообразное) изменение состояния 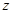. Этот принцип дает возможность существенно уменьшить затраты машинного времени на реализацию моделирующих алгоритмов по сравнению с принципом . Логика построения моделирующего алгоритма по принципу 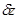включает в себя процедуру определения момента времени , соответствующего особому состоянию системы. При рассмотрении процессов функционирования некоторых систем можно выделить два типа состояний:

2. Особые, присущие системе только в некоторые моменты времени (поступления входных воздействий, возмущений внешней среды), функции состояния z= изменяются скачком.

2. Неособые, присущие системе в остальные моменты. Между особыми состояниями изменение состояний происходит плавно и непрерывно, или не происходит совсем.

Рассмотрим подробнее основные виды математических схем моделирования.