Непрерывно-стохастические модели

Непрерывно-стохастические модели (Q-схемы) реализуются схемами систем массового обслуживания (querring system, СМО). В качестве процесса обслуживания могут быть представлены различные по своей природе процессы функционирования экономических, производственных, технических и других систем, например потоки поставок продукции некоторому предприятию, потоки комплектующих на конвейере, заявки на обработку информации на ЭВМ и другие. Характерно, что появление заявок (требований) случайно, и завершение обслуживания происходит в случайные моменты времени.

В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки, поэтому -ый прибор обслуживания П_i состоит из накопителя заявок 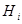, в котором может находиться одновременно заявок ( - емкость накопителя) и канала обслуживания . Потоком событий называется последовательность событий, происходящих одно за другим в случайные моменты времени. Поток называется однородным, если он характеризуется только моментами поступления этих событий (вызывающими моментами) и задается последовательностью , где 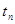- момент наступления n-го события. Поток называется неоднородным, если он зависит от моментов поступления и набора признаков события (принадлежности к определенному источнику заявок, наличия приоритета ограничений по типу канала обслуживания и др). На каждый элемент П_i поступают потоки событий, в накопитель - поток заявок , на канал - поток обслуживаний U_i. Процесс функционирования прибора представляется как процесс изменения состояний его элементов во времени , переход в новое состояние означает изменение количества заявок, которые в нем находятся. Для Q-схем, образованных композицией многих элементарных приборов используются сети массового обслуживания. Если каналы различных приборов обслуживания соединены параллельно, то Q-схема многоканальная, если П_i и их параллельные композиции соединены последовательно, то Q-схема многофазная. Связи между элементами Q-схемы изображают стрелками – линиями потока с направлением движения потока.

В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент (обратная связь отсутствует), в замкнутой Q-схеме имеются обратные связи, по которым заявки движутся в направлении, обратном движению «вход-выход».

Собственными параметрами Q-схемы является количество фаз L_ф, количество каналов в каждой фазе , количество накопителей каждой фазы , емкость -го накопителя .

Если , то есть накопитель в приборе П_i отсутствует, то СМО с потерями. Если 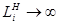, то есть накопитель имеет бесконечную емкость и очередь заявок не ограничена, то СМО с ожиданием. Если , то есть емкость накопителя ограничена, то СМО с ограниченным ожиданием.

Для задания Q-схемы необходимо описать алгоритм ее функционирования в различных ситуациях в зависимости от места их возникновения. Статические приоритеты назначаются заранее и независимы от состояний Q-схемы (фиксированы в конкретной задаче). Динамические приоритеты возникают в ходе работы модели. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель, ожидает окончания обслуживания предшествующей заявки каналом и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель , прерывает обслуживание каналом заявки с более низким приоритетом и сама занимает канал, вытесненная из заявка либо покидает систему, либо записывается на какое-либо место в накопитель .

При рассмотрении алгоритмов функционировании проборов обслуживания П_i (каналов и накопителей ) необходимо задать набор правил, по которым заявки покидают и : для - правила переполнения и ухода для - правила выбора маршрутов и направления ухода, правила блокировки канала, отражающие наличие управляющих связей в Q-схеме, регулирующих поток заявок.

Для оценки вероятностно-временных характеристик можно использовать аналитический аппарат, разработанный в теории массового обслуживания, но большими возможностями обладают имитационные модели на языках моделирования SIMULA, SIMSCRIPT, GPSS.

При исследовании СМО входящий поток требований обычно считают пуассоновским, характеризующимся интенсивностью , это означает, что требования поступают в случайные моменты времени, вероятность появления одного требования в интервале (t;t+Dt) равна и не зависит от , причем достаточно обосновано для практики, что вероятность появления в этом интервале двух и более требований пренебрежимо мала, длительности обслуживания требований предполагаются случайными с экспоненциальным законом распределения интенсивность обслуживания , то есть вероятность окончания обслуживания очередного требования в интервале (t;t+Dt) не зависит от и равна .

Уравнение

(*)

характеризует изменение за время общего числа систем , находящихся в состоянии , причем

- количество СМО в состоянии , на которые за время поступают новые требования, переводя их в состояние ;

- количество СМО, заканчивающих обслуживание заявок и переходящих в состояние из ;

- количество СМО, получивших новую заявку и перешедших из состояния в ;

- количество СМО, заканчивающих обслуживание заявок и переходящих в состояние из ;

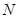- количество идентичных СМО;

- количество СМО в состоянии ;

- количество СМО в состоянии ;

- количество СМО в состоянии ;

тогда после деления уравнения (*) на , переходя к пределу при , получим уравнения «гибели и размножения»:

, при i 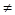0; i=0 соответственно,

применяемые для изучения изменения численности популяций в биологии, определения изменения характера обслуживания СМО.

Если СМО находится в стационарном состоянии, так называемом состоянии статического равновесия, тогда , то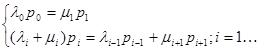

решение системы уравнений имеет вид: , где

Системы массового обслуживания могут быть классифицированы по ряду признаков:

1. В зависимости от условий ожидания начала обслуживания:

· СМО с отказами (потерями);

· СМО с ожиданием.

2. По числу обслуживающих каналов:

· одноканальные

· многоканальные.

3. По месту нахождения источника требований:

· разомкнутые, когда источник требований находится вне системы;

· замкнутые, когда источник находится в самой системе.

4. По количеству заявок в очереди:

· с ограниченной длиной очереди;

· с неограниченной длиной очереди.

Для СМО с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и теряются. Классическим примеромсистемы с отказами является телефонная станция. Если вызываемый абонент занят, то требование на соединение с ним получает отказ и теряется.

В СМО с ожиданием требование, застав все обслуживающие каналы занятыми, становится в очередь и ожидает, пока не освободится один из обслуживающих каналов.

СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ограниченной длиной очереди.

СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.

По способу отбора для обслуживания заявок из очереди различают следующие виды дисциплины очереди:

- первый пришел – первый обслуживается (FIFO);

- последний пришел - первый обслуживается (LIFO);

- ограничено время пребывания заявки в очереди;

- с приоритетами, при которых некоторые находящиеся в очереди заявки имеют право первоочередного обслуживания.

Основное содержание теории массового обслуживания составляют методы исследования характеристик СМО, находящихся под воздействием так называемых простейших потоков случайных событий. Одной из характеристик потока случайных событий является его интенсивность, или среднее число событий, происходящих в единицу времени. Для входного потока событий его интенсивность обозначается буквой l, а интенсивность обслуживания заявок одним каналом при непрерывной его работе обозначается m.

Простейшим называется поток случайных событий, обладающий тремя свойствами:

1.Стационарности, суть которого состоит в том, что вероятностные характеристики потока, в том числе его интенсивность, не зависят от времени.

2. Ординарности, означающее, что вероятность появления одного события за бесконечно малый промежуток времени dt является бесконечно малой величиной более высокого порядка.

3.Отсутствия последействия соответствует тому, что появление в потоке очередного события не зависит от того, когда появлялись в нем предшествующие события.

Одной из важнейших характеристик СМО является длина очереди. Для ее вычисления достаточно знать распределение вероятностей на множестве ее возможных дискретных значений: =L_ож

Для преобразования положим x=r/n, тогда

Найдем выражение для вычисления суммы:

при m®0

Другой важной характеристикой СМО является время обслуживания требований в системе. Время обслуживания одного требования является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и, особенно, в практических приложениях получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид: F(t) = 1-e ^–μt, означая вероятность того, что время обслуживания не превосходит некоторой величины t; μ – параметр экспоненциального закона распределения времени обслуживания требований в системе, μ = 1/ t_{ср. об .}

Вероятность обслуживания, называемая относительной пропускной способностью СМО, определяется как вероятность противоположного события по отношению к отказу:

Р_обсл = 1-Р_отк , где Р_отк = Р_R = Р_n+m = 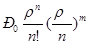, где R=n+m

Абсолютная пропускная способность системы А=Р_обслl, указывает среднее число заявок, обслуживаемых системой в единицу времени, n_ср = - среднее число каналов, занятых в системе обслуживанием заявок. Среднее число заявок, находящихся в системе, определим как сумму среднего числа заявок, ожидающих обслуживания, и среднего числа заявок под обслуживанием: L_s = L_ож + n_ср. Важнейшей характеристикой качества обслуживания является время пребывания заявки в системе, которое определяется формулой Литтла: W_s = , тогда W_q = 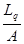- среднее время пребывания заявки в очереди.

Рассмотрим показатели эффективности работы СМО:

- экономическая эффективность Е=p_обслl с Т – G_n, где

С- средний экономический эффект от обслуживания одного требования;

Т – рассматриваемый интервал времени;

G_n- величина потерь в системе, причем:

- величина потерь для СМО с отказами G_n=(R_к M_з + R_уp_откl + R_пк M_св) Т, где

R_к – стоимость эксплуатации одного прибора обслуживания в единицу времени;

R_у - стоимость убытков в результате ухода требований из системы в единицу времени;

R_пк - стоимость простоя прибора в единицу времени;

M_з - среднее число занятых обслуживанием приборов;

M_св – среднее число свободных приборов;

- величина потерь для СМО с ожиданием G_n=(R_ож M_ож + R_к M_з + R_пк M_св) Т, где R_ож – стоимость потерь, связанных с простоем требований в очереди за единицу времени;

M_ож - среднее число требований, ожидающих начала обслуживания.

Рассмотрим основные модели СМО.