Непрерывно-детерминированные модели

Непрерывно-детерминированные модели или D-схемы (Dinamic) отражают динамику изучаемой системы, то есть ее поведение во времени, и описываются дифференциальными уравнениями, в которых независимой переменной неизвестных функций является время: , где f непрерывна и определена на n+1-мерном множестве ; - начальные условия.

Система автоматического управления – частный случай динамических систем, описываемых D-схемами. Структура многомерной системы автоматического управления имеет вид, представленный на рисунке 3.

Обозначим - вектор входных воздействий

- вектор возмущающих воздействий

- вектор сигналов ошибки

- вектор управляющих воздействий

- вектор состояния системы

- вектор выходных переменных

Рисунок 3 – Схема структуры системы управления

Современная управляющая система – это совокупность программно-технических средств, обеспечивающих достижение объектом управления определенной цели. О точности управления, например, для одномерной системы можно судить по координате состояния , а ошибка управления 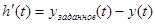. Системы, для которых ошибки управления называются идеальными, они не достижимы на практике. Задачей АСУ является изменение переменной с определенной точностью (допустимой ошибкой), для этого при проектировании АСУ необходимо выбирать параметры системы, способные обеспечить требуемую точность управления и устойчивость системы в переходном процессе.

При создании непрерывно-детерминированной модели рекомендуется применять следующую схему рассуждений:

1) Установить величины, изменяющиеся в рассматриваемом явлении или процессе и выявить законы, связывающие их.

2) Выбрать независимую переменную и функцию этой переменной, которую необходимо найти.

3) Исходя из условий задачи, определить начальные или краевые условия.

4) Выразить все величины, использованные в условии задачи, через независимую переменную, искомую функцию и ее производные, составить дифференциальное уравнение.

5) Найти общее решение, частное решение, исследовать полученные решения.

Пример. Шарик скатывается по гладкому желобу, изогнутому по циклоиде. Не учитывая сопротивление воздуха и трение, найти:

- зависимость пути, проходимого центром тяжести шарика, от времени;

- время движения шарика по желобу.

Сравнить с движением по отрезку АВ прямой, стягивающему желоб.

Решение.

Циклоида желоба имеет

уравнение:

Найдём проекцию всех сил, действующих на шарик, на касательную к циклоиде в произвольной точке траектории шарика.

Пусть касательная в рассмотренной точке наклонена под углом к оси Ох , тогда проекция силы тяжести F_т=mgSin . По II закону Ньютона F=ma, но используя физический смысл производной a=S˝(t), где S=S(t) – функция зависимости пройденного пути от времени, тогда mgSin =mS˝(t) или gSin =S˝(t), а, используя геометрический смысл производной, получаем tg =f ́(x), где f – кривая траектории, т.е.

тогда

.

Необходимо из этого уравнения исключить , выразив его через функцию S или её производные.

S(t) – длина дуги циклоиды, пройденной шариком за время t, тогда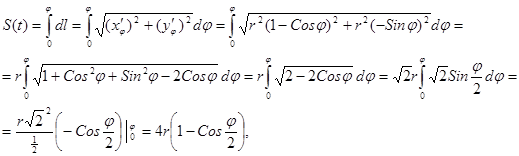

т.е. , тогда получаем дифференциальное уравнение:

,

- линейное неоднородное уравнение II порядка с постоянными коэффициентами. Решив это уравнение, получаем общее решение

Учитывая начальные условия S ́(0)=0 – скорость шарика в момент t=0, S(0)=0 – начальное перемещение шарика, получаем частное решение: .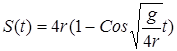

Длина циклоиды (желоба) (при 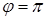) l=4r, тогда найдем t:

Сравним эти результаты со скатыванием шарика по отрезку АВ прямой:

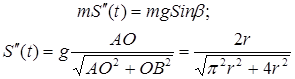
Учитывая начальные условия S ́(0)=0 и S(0)=0, получаем

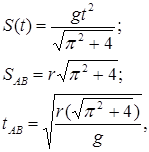
откуда видно, что .