Дискретно-стохастические модели

Дискретно-стохастические модели (Р-схемы) (probabilistic automat)реализуются вероятностными автоматами, являются дискретными потактными преобразователями информации с памятью, функционирование которых в любом такте зависит только от состояния памяти в нем и может быть описано статистически. Р-схемы применяются для проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выявления алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, для решения задач синтеза по выбранному критерию дискретных стохастических систем.

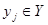Определение. Пусть ,где - множество входов, а - множество состояний, , где - множество выходов. Пусть существует закон распределения, указывающий вероятности переходов из в

			…..
			…..

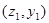
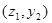
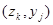
или

Y Z			…..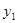
			…..
			…..
…..	…..	…..	…..	…..
			…..

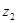
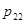
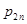
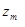
где ; - вероятность перехода автомата в состояние и появление на выходе сигнала , если бы он был бы в состоянии , и на его вход в этот момент времени поступил сигнал . Число таких распределений, представленных в виде таблиц, равно числу элементов множества . Если обозначить В - множество таблиц распределений, то множество Р={Z,X,Y,B} - вероятностный автомат.

Таблицы множества переформируем следующим образом:

Элементы Y			…..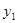
			…..
Элементы Z			…..
			…..

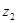
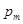
где и - вероятности перехода автомата Р в состояние и появления выходного сигнала соответственно, при условии, что автомат находится в состоянии 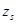, и на его вход поступил входной сигнал , причем .

Если 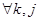, то автомат называется вероятностным автоматом Мили (существует независимость распределений для нового состояния автомата и его выходного сигнала)

Если закон распределения выходов имеет вид:

Элементы			….
			….

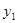
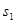
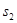
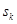
то есть определение выходов зависит лишь от состояния, в котором находится автомат в данном такте работы, тогда если 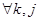, то автомат называется вероятностным автоматом Мура.

Частным случаем Р-автомата являются автоматы, у которых переход в новое состояние детерминирован (Z-детерминированный автомат) или выходной сигнал детерминирован (Y-детерминированный автомат). Подобные P-автоматы могут использоваться как генераторы марковских последовательностей, необходимых при построении и реализации процессов функционирования систем или воздействий внешней среды. Для оценки характеристик исследуемых систем могут применяться аналитические модели и имитационные модели.

Y-детерминированный P-автомат может быть задан таблицей переходов

Z			…..
			…..
			…..
…..	…..	…..	…..	…..
			…..

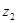
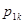
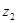
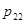
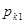
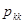
таблицей выходов

Z			…..
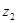
Y			…..

причем необходимо задать начальное распределение вероятностей нахождение автомата в состоянии :

Z			…..
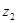
P			…..

считая, что до начала работы (до нулевого такта времени) P-автомат всегда находится в состоянии и в нулевой такт времени меняет состоянии с этим распределением, а дальнейшая смена состояний P-автомата определяется матрицей переходов , иногда для удобства начальная информация также входит в :

.

Y-детерминированный P-автомат можно задать определенным графом, вершины которого – состояние автомата, дуги возможные переходы из состояния в состояние вес дуг – вероятности перехода 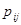пометки около вершин - значения выходных сигналов, индуцируемых этими состояниями. [18]

Пример. Пусть автомат задан матрицей

Z
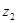
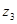
Y

Тогда граф P-автомата имеет вид: