СМО с отказами.

Последовательностьмодельного описания базируется на представлении о конечном множестве состояний системы (S₀, S_1, S₂, S₃, …, S_k, …, S_n) и исходных данных по некоторым параметрам, таких, как λ, μ, n. На этом основании можно пользоваться моделями и методами теории массового обслуживания для определения других показателей СМО.

Для определения вероятности или времени простоя каналов обслуживания, т.е. когда нет заявок, и система находится в состоянии S₀, следует пользоваться формулой: Р₀ = [ ρ^k / k!]^-1, а для определения вероятности занятости k каналов обслуживания (нахождения k требований в системе) применяют формулу: Р_k = ρ^k p_o / k!.

Вероятность отказа в обслуживании определяется вероятностью того, что поступившая на обслуживание заявка найдет все каналы занятыми, т.е. система будет находиться в состоянии S_n: Р_отк = Р_n = ρⁿ/n!*Р₀, т.е. k=n.

В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: Р_отк + Р_обс = 1 или Р_обс = 1-Р_отк.

Вероятность обслуживания или доля обслуженных заявок определяет относительную пропускную способность q: q = P_обс = n_з / ρ. Отсюда можно определить среднее число занятых обслуживанием каналов: n_з = ρ P_обс, или . Абсолютную пропускную способность СМО можно определить по формуле: А = λ*Р_обс.

Пример. В вычислительный центр с тремя ЭВМ поступают заказы на выполнение работы. Если работают все три ЭВМ, то вновь заказы не принимаются. Среднее время работы с одним заказом 3 часа, интенсивность потока заявок λ=1/4 (1/ч); μ=1/3 (1/ч). Найти Р_отк; М_з.

Решение:

ρ=λ/μ = 0,75.

Р₀ = [1+0,75+(0,75)² / 2! + (0,75)³/ 3!]^-1 = [2,1]^-1.

Р_отк = Р_n= (0,75)³/ 3!*[2,1]^-1 = 0,033.

м_з = i*p_i = p₀ ρⁱ / (i-1)! = 0,72 .

СМО с ожиданием –это СМО, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, становятся в очередь и обслуживаются по мере освобождения каналов. Общая постановка задачи состоит в следующем. Система имеет nобслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование. В систему поступает простейший (пуассоновский) поток требований с параметром λ. Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.

Время обслуживания каждого требования t_об – случайная величина, которая подчиняется экспоненциальному закону распределения с параметром μ.

СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. К замкнутым СМО относятся системы, в которых поступающий поток требований возникает в самой системе и ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится потенциальным источником требований на наладку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно.

Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами таких систем могут служить магазины, кассы вокзалов, портов и т.д. Для этих систем поступающий поток требований можно считать неограниченным. При изучении таких систем рассчитывают различные показатели эффективности обслуживающей системы. В качестве основных показателей могут быть: вероятность того, что все каналы свободны или заняты, математическое ожидание длины очереди (средняя длина очереди), коэффициенты занятости и простоя каналов обслуживания и др.

Введем в рассмотрение параметр ρ= λ/μ. Заметим, что если ρ /n < 1, то очередь не может расти безгранично. Это условие имеет следующий смысл: λ – среднее число требований, поступающих за единицу времени, 1/μ – среднее время обслуживания одним каналом одного требования, тогда: ρ= λ*1/μ – среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования. Поэтому условие ρ /n < 1 означает, что число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования. Важнейшие характеристики работы СМО:

1. Вероятность того, что все обслуживающие каналы свободны

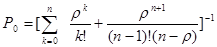
2. Вероятность того, что занято ровно k обслуживающих каналов при условии, что общее число требований, находящихся на обслуживании, не превосходит числа обслуживающих аппаратов

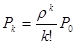при

3. Вероятность того, что в системе находится k требований в случае, когда их число больше числа обслуживающих каналов

при

4. Вероятность того, что все обслуживающие каналы заняты

при ρ /n < 1

5. Среднее время ожидания требованием начала обслуживания в системе

6. Средняя длина очереди

при ρ /n < 1

7. Среднее число свободных от обслуживания каналов

8. Коэффициент простоя каналов

9. Среднее число занятых обслуживанием каналов

10. Коэффициент загрузки каналов

11. Среднее количество требований, ожидающих начала обслуживания:

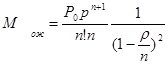
12. Общее количество требований, находящихся в системе

M=m_з+М_ож

Пример. В порту есть два причала для разгрузки грузовых судов. Интенсивность разгрузки 2 суток для 1 судна, поток заявок описывается λ=0,8ед/сут. Очередь ожидающих имеет неограниченную длину. Найти среднее число занятых причалов и среднее время пребывания судна в порту.

Решение: λ = 0,8; μ = 1/Т = ½ = 0,5; ρ = λ/μ = 1,6; n = 2; ρ/n = 1,6/2<1.

Р₀ = [1+1,6/1!+1,6²/2!+1,6³/2!(2-1,6)]^-1 = 0,11

m_з = ρ*q = 1,6*(1-Р_отк) = 1,6, при Р_отк = 0.

М_ож = 2,8.

Т_ож = M_ож / λ = 3,5.

Пример. Пусть в филиале фирмы по ремонту радиоаппаратуры работает n = 5 опытных мастеров. В среднем в течение рабочего дня от населения поступает в ремонт λ = 10 радиоаппаратов. Общее число радиоаппаратов, находящихся в эксплуатации у населения, очень велико, и они независимо друг от друга в различное время выходят из строя. Поэтому есть все основания полагать, что поток заявок на ремонт аппаратуры является случайным, пуассоновским. В свою очередь каждый аппарат в зависимости от характера неисправности также требует случайного времени на ремонт. Время на проведение ремонта зависит во многом от серьезности полученного повреждения, квалификации мастера и множества других причин. Пусть статистика показала, что время ремонта подчиняется экспоненциальному закону; при этом в среднем в течение рабочего дня каждый из мастеров успевает отремонтировать μ = 2,5 радиоаппарата. Требуется оценить работу филиала фирмы по ремонту радиоаппаратуры, рассчитав ряд основных характеристик данный СМО.

Решение. За единицу времени принимаем 1 рабочий день (7 часов).

1. Определим параметр

ρ = λ*(1/μ) = 10*(1/2,5) = 4,

так как ρ<n, то очередь не может расти безгранично.

2. Вероятность того, что все мастера свободны от ремонта аппаратуры, равна

Р₀ = 1 / 1+4+4²/2!+4³/3!+4⁴/4!+4⁵/5!(1-4/5) = 0,013

3. Вероятность того, что все мастера заняты ремонтом, равна

Р_n = 4⁵*0,013 / 5!(1-4/5) = 0,554

Это означает, что 55,4% времени мастера полностью загружены работой.

4. Среднее время обслуживания (ремонта) одного аппарата равно

t_{ср об} = (1/μ)*7 = (1/2,5)*7 = 2,8 ч/аппарат

(при условии семичасового рабочего дня)

5. В среднем время ожидания каждым неисправным аппаратом начала ремонта равно t_{ср ож} = 0,554*2,8 /(5-4) = 1,55ч

6. Длина очереди L_{ср оч} = 0,554*4 / 5(1-4/5) = 2,2аппарата

7. Среднее число мастеров, свободных от работы

N_{ср 0} = 0,013 [5-0/1*1+5-1/1!*4+5-2/2!+4²+5-3/3!*4³+5-4/4!*4⁴ ] = 0,95

Таким образом, в среднем в течение рабочего дня ремонтом заняты 4 мастера из 5.

Рассмотрим алгоритм расчета характеристик функционирования замкнутых СМО. Поскольку система замкнутая, то к постановке задачи следует добавить условие: поток поступающих требований ограничен, т.е. в системе обслуживания одновременно не может находиться больше m требований (m – число обслуживаемых объектов). Источник требований находится внутри самой системы, и интенсивность потока требований зависит от состояния системы. Потоком требований чаще всего является поток неисправностей в группе работающих устройств.

За критерий, характеризующий качество функционирования рассматриваемой системы, выберем отношение средней длины очереди к наибольшему числу требований, находящихся одновременно в обслуживающей системе – коэффициент простоя обслуживаемого объекта. В качестве другого критерия возьмем отношение среднего числа незанятых обслуживающих каналов к их общему числу – коэффициент простоя обслуживаемого канала.

Первый из названных критериев характеризует потери времени из-за ожидания начала обслуживания; второй показывает полноту загрузки обслуживающей системы. Очевидно, что очередь может возникнуть, лишь, когда число каналов меньше наибольшего числа требований, находящихся одновременно в обслуживающей системе (n<m).

Приведем последовательность расчетов характеристик замкнутых СМО и необходимые формулы:

1. Определим параметр ρ = λ/μ – показатель загрузки системы, т.е. математическое ожидание числа требований, поступающих в систему за время, равное средней длительности обслуживания (1/μ = t_{ср об}).

2. Вероятность того, что занято k обслуживающих каналов при условии, что число требований, находящихся в системе, не превосходит числа обслуживающих каналов n системы:

3. Вероятность того, что в системе находится k требований для случая, когда их число больше числа обслуживающих каналов

при

4. Вероятность того, что все обслуживающие каналы свободны, определим, используя очевидное условие:

откуда

Величину P₀ можно получить также путем подстановки в равенство значений Р₁, Р₂, …, Р_m, в которые Р₀ входит сомножителем. Подставляя их, получаем следующее уравнение для определения Р₀:

откуда

5. Среднее число требований, ожидающих начала обслуживания (средняя длина очереди):

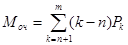
или

6.Коэффициент простоя обслуживаемого требования (объекта)

7. Среднее число требований, находящихся в обслуживающей системе, обслуживаемых и ожидающих обслуживания:

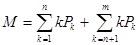
или

8. Среднее число свободных обслуживающих каналов

9. Коэффициент простоя обслуживающего канала

Вероятности состояний:

, при i=

, при i=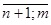

Для этой модели СМО существуют специальные формулы вычисления показателей работы:

1. Среднее число заявок на обслуживании

2. Среднее число заявок, ожидающих обслуживание

3. Среднее время простоя источника заявок

где вероятность простоя заявок

4. Среднее время простоя канала обслуживания

, где вероятность простоя канала.

5. Среднее время ожидания заявки в очереди t_оч= t_{пр источника}- 1/μ

Пример. Рабочий обслуживает группу из 3 станков. Каждый станок останавливается в среднем 2 раза/ч и процесс наладки занимает в среднем 10мин. Определить абсолютную пропускную способность наладки рабочим станков.

Решение: n-1, m=3, λ=2, μ=6. ρ=1/3.

A=μ*P_з=μ(1-Р₀); Р₀ = 0,346; А = 6(1-0,346) = 4.

СМО с неограниченным ожиданием.Для ниххарактерно отсутствие отказа в обслуживании, т.е. Р_отк=0, а, следовательно, все заявки будут обслужены. Поэтому Р_обс=1, и относительная пропускная способность q=1. При этом абсолютная пропускная способность определяется выражением А = Р_обс*λ = λ.

Вероятность того, что СМО находится в состоянии S₀, когда нет заявок, т.е. не занят ни один канал Р₀ = [ ρ^k / k! + ρⁿ⁺¹ /(n! (n-ρ))]^-1.

Вероятность занятости обслуживанием к заявок: Р_к = ρ^к / к! * Р₀ . На этом основании вероятность или доля времени занятости обслуживанием всех каналов системы равна Р_n =ρⁿ / n!*Р₀

Если же каналы уже заняты обслуживанием, то вероятность состояния

Р_к=ρ^к /( n!n^k-n )* Р_о, где величина (k-n) определяет длину очереди l_оч, тогда вероятность оказаться в очереди равна вероятности застать все каналы уже занятыми обслуживанием. Среднее число занятых обслуживанием каналов

n_ср = А/μ=ρ

Для СМОс ограниченным временем ожидания

,где n – число каналов обслуживания. [18, 21, 28]