Разыгрывание дискретных случайных величин

Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. С этой целью выбирают такую случайную величину Х, математическое ожидание которой равно а: М(Х)=а.

Практически же поступают так: вычисляют (разыгрывают) n возможных значений x_i случайной величины Х, находят их среднее арифметическое

и принимают в качестве оценки (приближенного значения) а* искомого числа а. Таким образом, для применения метода Монте-Карло необходимо уметь разыгрывать случайную величину.

Пусть требуется разыграть дискретную случайную величину Х, т.е. вычислить последовательность ее возможных значений х_i (i=1,2, …), зная закон распределения Х. Введем обозначения: R- непрерывная случайная величина, распределенная равномерно в интервале (0,1); r_i (j=1,2,…) – случайные числа (возможные значения R).

Правило: Для того чтобы разыграть дискретную случайную величину Х, заданную законом распределения

Х х₁ х₂ … х_n

P p₁ p₂ … p_n

надо:

1. Разбить интервал (0,1) оси or на n частичных интервалов:

Δ₁ =(0;р₁), Δ₂=(р₁; р₁₊р₂), …, Δ_n= (р₁+р₂+…+р_n-1; 1).

2.Выбрать случайное число r_j. Если r_j попало в частичный интервал Δ_i, то разыгрываемая величина приняла возможное значение х_i..

Разыгрывание полной группы событий

Требуется разыграть испытания, в каждом из которых наступает одно из событий полной группы, вероятности которых известны. Разыгрывание полной группы событий сводится к разыгрыванию дискретной случайной величины.

Правило: Для того чтобы разыграть испытания, в каждом из которых наступает одно из событий А_1, А_2, …, А_n полной группы, вероятности которых р_1, р₂, …, р_n известны, достаточно разыграть дискретную величину Х со следующим законом распределения:

Х 1 2 … n

P p₁ p₂ … p_n

Если в испытании величина Х приняла возможное значение x_i=i, то наступило событие А_i.

Разыгрывание непрерывной случайной величины

Известна функция распределения F непрерывной случайной величины Х. Требуется разыграть Х, т.е. вычислить последовательность возможных значений х_i (i=1,2, …).

А. Метод обратных функций. Правило 1. Для того чтобы разыграть возможное значение х_i непрерывной случайной величины Х, зная ее функцию распределения F, надо выбрать случайное число r_i, приравнять его функции распределения и решить относительно х_i полученное уравнение F(х_i) = r_i.

Если известна плотность вероятности f(x), то используют правило 2.

Правило 2. Для того чтобы разыграть возможное значение х_i непрерывной случайной величины Х, зная ее плотность вероятности f, надо выбрать случайное число r_i и решить относительно х_i уравнение

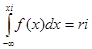
или уравнение

где а – наименьшее конечное возможное значение Х.

Б. Метод суперпозиции. Правило 3. Для того чтобы разыграть возможное значение случайной величины Х, функция распределения которой

F(x) = C₁F₁(x)+C₂F₂(x)+…+C_nF_n(x),

где F_k(x) – функции распределения (k=1, 2, …, n), С_k>0, С_i+С₂+…+С_n=1, надо выбрать два независимых случайных числа r₁ и r₂ и по случайному числу r₁ разыгрывать возможное значение вспомогательной дискретной случайной величины Z (по правилу 1):

Z 1 2 … n

p C₁ C₂ … C_n

Если окажется, что Z=k, то решают относительно х уравнение F_k(x) = r₂.

Замечание 1. Если задана плотность вероятности непрерывной случайной величины Х в виде

f(x)=C₁f₁(x)+C₂f₂(x)+…+C_nf_n(x),

где f_k – плотности вероятностей, коэффициенты С_k положительны, их сумма равна единице и если окажется, что Z=k, то решают (по правилу 2) относительно х_i относительно или уравнение

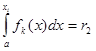
Приближенное разыгрывание нормальной случайной величины

Правило. Для того чтобы приближенно разыграть возможное значение х_i нормальной случайной величины Х с параметрами а=0 и σ=1, надо сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:

Замечание. Если требуется приближенно разыграть нормальную случайную величину Z с математическим ожиданием а и средним квадратическим отклонением σ, то, разыграв возможное значение х_i по приведенному выше правилу, находят искомое возможное значение по формуле: z_i=σx_i+a.[2]