Способы рандомизации

1) Аппаратный способ предполагает, что случайные числа вырабатываются специальной приставкой - датчиком случайных чисел, основа этих генераторов – шумы в электронных и полупроводниковых проборах, явление распада радиоактивных элементов и другие случайные процессы.

Структурная схема генератора случайных чисел изображена на рис. 6.

Рисунок 6 – Схема генератора случайных чисел.

При усилении шумов на выходе источника шума получается напряжение , являющееся случайным процессом, шумовая реализация с помощью ключевой схемы содержит случайное число выбросов. Сравнение с пороговым позволяет сформировать серию импульсов , тогда на выходе пересчетной схемы получается последовательность случайных чисел .

Если принять за единицу длину интервала 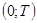, между соседними импульсами будут случайные числа .

Но этот способ не позволяет гарантировать качество последовательности случайных чисел или повторно получать при моделировании одинаковые последовательности случайных чисел.

2) Табличный способ рационально использовать при небольшом объеме таблицы случайных чисел, когда для хранения случайных чисел можно применять оперативную память.

3) Алгоритмический способ основан на формировании случайных чисел с помощью специальных алгоритмов в ЭВМ, но так как алгоритмы используют формулы, то последовательности приобретают характер детерминированности, являются псевдослучайными.

Общие требования к генератору случайных чисел:

1. Последовательность случайных величин состоит из квазиравномерно распределенных чисел:

2. Статистическая независимость.

3. Воспроизводимость.

4. Неповторяемость.

5. Минимальные затраты машинного времени.

6. Минимальный объем памяти.

Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации случайных величин. Два числа и называются конгруэнтными (сравнимыми) по модулю , т.е. , если или числа и имеют одинаковые остатки при делении на , тогда рекуррентная функция для случайной величины примет вид , где ; - заданы. Процедура получения псевдослучайных, квазиравномерно распределенных чисел реализуются:

1) Мультипликативным методом

Для машинной реализации наиболее удобна версия , где - число цифр в системе счисления; - число битов в машинном слове, тогда вычисление остатка от деления не сводится к выделению младших разрядов делимого, а преобразование в рациональную дробь из промежутка 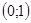осуществляется подстановкой слова и справа от двоичной или десятичной запятой.

При существует алгоритм:

1. Выбрать - нечетное

2.

3. Принять с не более чем значащими разрядами.

4. Взять младших разрядов в качестве

5. Определить дробь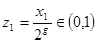

6.

7. Вернуться к пункту 3.

2) Смешанным методом , предусматривающим мультипликативный метод со сложением, что позволяет уменьшить возможную корреляцию чисел.

Результаты анализа систем при помощи статистического моделирования на ЭВМ существенно зависят от качества псевдослучайных чисел, поэтому необходимо тщательно тестировать генератор случайных чисел на равномерность, стохастичность и независимость.

Проверка на равномерность ППКРСЧ (последовательности псевдослучайных квазиравномерно распределенных случайных чисел) проводится:

1) По гистограмме: при достаточно больших 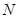кривая гистограммы должна приблизится к теоретической прямой , оценка степени приближенности проводится по критериям согласия, принимая - количество интервалов разбиения; - объем последовательности.

2) По косвенным признакам генерируемая последовательность разбивается на две подпоследовательности:

и если , то - счетчик (точка четверти круга с ).

В общем случае точка всегда попадает внутрь квадрата со стороной равной 1, тогда . При - равномерной, в силу закона больших чисел,

Проверка стохастичности производится:

1. Методом комбинаций, когда определяется закон распределения длин участков между единицами (нулями) или распределения числа единиц (нулей) в -разрядном двоичном числе теоретически закон появления единиц в разрядных числах описывается, исходя из независимости отдельных разрядов, биномиальным законом распределения , , тогда наиболее вероятное число появлений случайных чисел с единицами в разрядах , а затем проверяется гипотеза о стохастичности по критериям согласия для теоретических и экспериментальных вероятностей .

2. Методом серий, когда последовательность разбивается на элементы первого и второго рода (a и b):

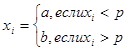
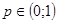
Серией называют любой отрезок последовательности, состоящий из идущих друг за другом элементов одного рода, число элементов в серии называется ее длиной.

Из независимости случайных чисел и следует возможность применения формулы Бернулли для вычисления вероятности появления серии длиной в последовательности длиной . И экспериментальные значения принимаются как частоты появления серий длиной .

При различных значениях и проводят проверку зависимости и по критериям согласия.

Проверка независимости. Элементов ППКРСЧ проводится на основе вычисления корреляционных методов и коэффициентов корреляции ,

где ;

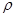Для достаточно больших N с доверительной вероятностью справедливо . Если найденное находится в этих пределах, то с вероятностью можно утверждать, что - последовательность независимых чисел.

Важнейшими характеристиками качества генератора являются длина периода и длина отрезка апериодичности , в пределах которого все числа не повторяются. Если , то повторение испытаний происходит в тех же условиях и увеличение числа реализаций не дает новых статистических результатов. Расчетные соотношения для определения и не получены в явном виде, экспериментальное определение громоздко, поэтому используют вероятностную модель.

Если имеется конечное множество 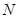различных чисел, тогда вероятность увеличения любого числа равно . Пусть случайная величина, означающая номер опыта, в котором впервые снова извлечено уже записанное ранее число, тогда , тогда , а при - грубая оценка длины отрезка апериодичности, которую можно уточнить экспериментально следующим образом: генерируются чисел , затем с программа запускается повторно и при генерации очередного числа проверяется условие ; продолжаем процесс, пока это условие не выполнится дважды при и , тогда . Проводя запуск генерации с начальными числами и , фиксируем номер (минимальный), при котором , тогда .

В теории чисел замечено, что при простом модуле и последовательности чисел , если взаимно просто с , тогда нужно найти при каких условиях равенство справедливо при минимальном значении известно, что , тогда при , если .[18]