
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение регрессионной модели
Пусть результаты моделирования представлены в виде:
| x | x1 | x2 | x3 | ..... | xn |
| y | y1 | y2 | y3 | yn |
Не существует общего правила для выбора подходящей эмпирической формулы зависимости у=f(х). Можно:
1) изобразить все значения в корреляционном поледля выяснения вида формулы;
2) использовать различные средние значения показателей эмпирического ряда (среднее арифметическое, среднее геометрическое, среднее гармоническое первого и последнего значения), вычисленные для различных видов зависимости
| Форма связи | Уравнение регрессии | хs | ys |
| Линейная | у=aх+b | 
| 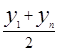
|
| Гиперболическая | y=a/x+b | 
| 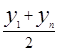
|
| Полулогарифми-ческая | y=a lg x+b | 
| 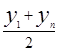
|
| Показательная | y=ax b | 
| 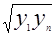
|
| Степенная | y=b xa | 
| 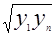
|
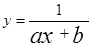
| 
| 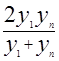
| |
| Логистическая | 
| 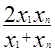
| 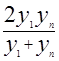
|
Находят у(  )=
)= 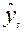 , если
, если 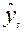 нет среди табличных значений, то находят с помощью линейной интерполяции
нет среди табличных значений, то находят с помощью линейной интерполяции  . Если величина
. Если величина 
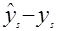 | большая, то соответствующая эмпирическая формула не пригодна.
| большая, то соответствующая эмпирическая формула не пригодна.
3) выбирают наименьшее уклонение данных от прямой Y=kX+h 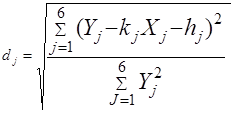 , где Yj, Xj – новые переменные зависимости Y=kX+h, полученные при помощи выравнивания данных:
, где Yj, Xj – новые переменные зависимости Y=kX+h, полученные при помощи выравнивания данных:
| Форма связи | Уравнение регрессии | Выравнивание данных |
| Гиперболическая | y=a/x+b | X=x Y=xy |
| Полулогарифми-ческая | y=a lg x+b | X=lg x Y=y |
| Показательная | y=ax b | X=x Y=ln y |
| Степенная | y=b xa | X=ln x Y=ln y |
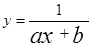
| X=x Y=1/y | |

| X=x Y=x/y |
Выбрав наиболее подходящий вид зависимости, находят ее параметры методом наименьших квадратов из системы нормальных уравнений:
| Форма связи | Уравнение регрессии | Система нормальных уравнений |
| Линейная | у=aх+b |  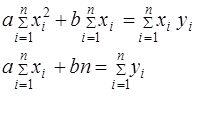
|
| Квадратичная | y=ax2+bx+c | 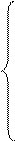 
|
| Гиперболическая | y=a/x+b |  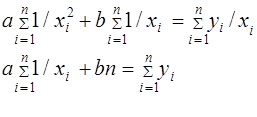
|
| Полулогарифми-ческая | y=a lg x+b | 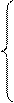 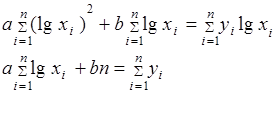 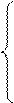
|
| Показательная | y=ax b |  
|
| Степенная | y=b xa | 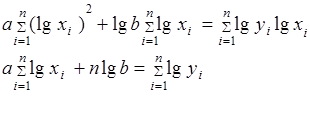 
|
Дата добавления: 2015-01-05; просмотров: 279; Мы поможем в написании вашей работы!; Нарушение авторских прав |