Сетевые модели

Для решения задач, связанных с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно протекает несколько процессов, используются сети Петри (Petri Nets). Сети Петри применяются для моделирования систем принятия решений, политических систем, макроэкономических событий, транспортных и информационных потоков, логистических систем, изучения химических реакций, военных конфликтов, биологических популяций, процессов функционирования мозга.

Формально сеть Петри (N- схема) задается четверкой множеств , где

- конечное непустое множество символов-позиций,

- конечное непустое множество символов-переходов, множество не пустое,

- входная функция (прямая функция инцидентности)

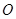- выходная функция (обратная функция инцидентности)

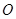Входная функция отображает переход в множество входных позиций , выходная функция отображает переход в множество выходных позиций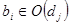

Графически N-схемы изображаются в виде двудольного ориентированного мультиграфа, представляющего собой совокупность двух типов узлов: позиций и переходов (изображаются 0 и 1соответственно). N-схема позволяет отразить статику моделируемой системы - взаимосвязь условий и событий, и не позволяет отразить динамику функции моделируемой системы. Для представления динамических свойств объекта вводится функция маркировки (разметки), обозначаемая . Маркировка ( ) – это присвоение неких абстрактных объектов, называемых метками (фишками), позициям N-схемы, причем количество меток, соответствующее каждой позиции, может меняться. Разметка отображается соответствующим числом точек, или числом внутри вершины позиции. Функционирование N-схемы отражается путем перехода от разметки к разметке.

Смена разметок происходит в результате срабатывания одного из переходов сети. Необходимым условием срабатывания перехода является , где - разметки позиции . Переход , для которого выполняется указанное условие, определяется как возбужденный переход или переход, готовый к срабатыванию. Срабатывание перехода изменяет разметку сети на разметку 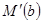по следующему правилу: , то есть переход удаляет по одной метке из каждой входной позиции и добавляет по одной метке в каждую входную позицию. Для изображения сметы разметки на применяется обозначение , то есть функционирование N-схемы выполняется путем запусков переходов под управлением количества меток и их распределения в сети. Переход запускается удалением меток из его входных позиций и образованием новых меток, помещаемых в выходные позиции. Переход разрешен, если в каждой из входных позиций N-схема имеет число меток, равное по крайне мере числу дуг из позиции в переход.

Динамика сетей Петри обусловлена правилами срабатывания переходов:

- выполняется только возбужденный переход (во всех его входных позициях имеются ненулевые метки);

- срабатывание перехода может наступить через любой конечный промежуток времени после его возбуждения;

- если в некотором состоянии сети возбужденными оказываются сразу несколько переходов, то всегда выполняется только один из них;

- в результате срабатывания перехода метки в каждой входной позиции уменьшаются на единицу, а метки во всех его выходных позициях увеличиваются на единицу;

- выполнение перехода – неделимый акт, изменение разметки входных и выходных позиций перехода при его выполнении (срабатывании) осуществляется мгновенно.[12, 24]

Пример. Представим N-схему в виде графа. ;

- позиции;

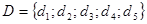- переходы;

от к (от 0 к 1)

от к (от 1 к 0)

Пример. Пусть N-схема имеет первоначальную разметку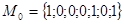

при такой начальной разметке N-схемы единственным готовым к срабатыванию является переход , его срабатывание ведет к смене разметки , где

При разметке возможно срабатывание переходов .

В зависимости от того, какой переход сработал первым, получается одна из трех возможных новых маркировок:

1) M₂={1;0;1;0;1;0;1} , где М₁d₁M₂

2) M₃={0;1;0;1;0;0;1} , где М₁d₃M₃

3) M₄={0;1;0;0;1;1;0} , где М₁d₅M₄

Функционирование N-схемы продолжается до тех пор, пока существует хотя бы один возможный переход.

Типовые N-схемы используются при построении иерархических конструкций модели, при моделировании параллельных конкурирующих процессов в различных системах. N-схема может рассматриваться как макропереход или макропозиция модели более высокого уровня, а переход или позиция N-схемы может детализироваться в форме отдельной подсети для углубленного исследования процессов в моделируемой системе S для событий произвольной длительности, так как отражает только порядок поступления событий в исследуемой системе S. Для отражения временных параметров процесса функционирования моделируемой системы на базе N-схем используется расширения аппарата сетей Петри: E-сети, сети Мерлина.[18]

Пример. Станок для обработки заготовок имеет магазин инструментов и оснащен средствами автоматической замены и подготовки инструмента к работе. Заготовки в таре поступают в накопитель 4, откуда с помощью ПР (промышленного робота) переносятся в позицию 1 загрузки станка. Освободившаяся при этом тара также с помощью ПР подается в зону выхода детали после обработки. Готовая деталь помещается в тару и с помощью ТМ (трансманипулятора) перемещается в накопитель 7 готовых деталей. Освободившийся после выполнения этой операции ТМ забирает на месте комплектации 5 очередную заготовку в таре и доставляет ее в накопитель. Представим процесс на рис. 4, 5.

Рисунок 4 - Описание процесса функционирования производственного модуля через условия и события.

Рисунок 5 - Описание процесса функционирования производственного модуля в виде сети Петри.

Позиции имеют следующий смысл:

b₁ – заготовка закреплена на станке и готова к обработке;

b₂ – инструмент подготовлен для выполнения операции;

b₃ – выдан запрос об условиях обработки очередной заготовки;

b₄ – ПР свободен;

b₅ – разрешена замена инструмента;

b₆ - тара свободна;

b₇ - ПР свободен;

b₈ – пустая тара установлена на выходе станка;

b₉ – выполняется программа обработки детали;

b₁₀ - деталь обработана;

b₁₁ – ТМ выполняет программу 1: захватывает готовую деталь, помещает ее в тару, движется к накопителю 7, разгружается в накопитель;

b₁₂ – ТМ свободен;

b₁₃ – выдан запрос об очередной заготовке, которую необходимо доставить в зону обработки;

b₁₄ – получены данные о типах заготовки и тары, адреса их хранения;

b₁₅ – очередная заготовка в таре подготовлена и находится на месте комплектации;

b₁₆ – позиция для приема новой заготовки и тары для нее на месте комплектации подготовлена;

b₁₇ – ТМ выполняет программу 2: берет тару с заготовкой в накопителе 5, переносит ее в накопитель 4, разгружается в накопителе 4;

b₁₈ – тара с заготовкой находится в накопителе 4;

b₁₉ – ТМ свободен.

Переходы имеют следующий смысл:

d₁ – ПР выполняет программу 1: берет заготовку из тары в накопителе 4, закрепляет ее на станке;

d₂ – включение программы обработки детали;

d₃ – ПР выполняет программу 2: берет пустую тару из накопителя 4, переносит ее на выход станка в зону 2, фиксирует тару в зоне 2;

d₄ – выполнена программа подготовки инструмента к обработке очередной заготовки;

d₅ – выполнена программа обработки детали;

d₆ – включается программа 1 управления ТМ;

d₇ – выполнена программа 1 управления ТМ;

d₈ – включается программа 2 управления ТМ;

d₉ – выполняется программа по определению данных о типах очередной заготовки и соответствующей тары, адресов их хранения;

d₁₀ – выполняется программа подготовки на месте комплектации очередной заготовки в таре;

d₁₁ – выполнена программа 2 управления ТМ.

Начальное состояние рассматриваемой сети описывается следующим образом: ПР закончил выполнение операции по переносу пустой тары в зону 2 из накопителя 4 и освободился для выполнения следующей операции своего производственного цикла (условие b₄ выполнено); пустая тара под готовую деталь установлена в выпускной зоне станка (условие b₈ выполнено); деталь прошла обработку (условие b₁₀ выполнено); очередная заготовка в таре ожидает на месте комплектации 5 (условие b₁₅ выполнено); поступил сигнал, разрешающий замену инструмента (условие b₅ выполнено); ТМ доставил заготовку в таре с места комплектации в накопитель 4 и освободился для выполнения очередной операции своего производственного цикла (условие b₁₉ выполнено), тогда начальная разметка имеет вид: М₀=(0001100101000010001). Возбужденным оказывается переход d₆, и получаем после его срабатывания разметку М₁=(0001100000100010000). Теперь возбужденным оказывается переход d₇, после его срабатывания получим разметку М₂=(0001100000010010000) и т.д.[24]

1.6 Модели сетевого планирования и управления (СПУ)

При планировании сложных комплексов взаимосвязанных и взаимообусловленных работ и управления ходом их выполнения наиболее эффективны модели и методы сетевого планирования и управления (СПУ). Основой методов СПУ является представление комплекса работ при помощи сетевого графика – ориентированного графа, представляющего взаимосвязь работ комплекса. Вершины графа - события, дуги (ориентированные ребра) – операции (работы), вес дуги – время выполнения работы, расход ресурса, количество исполнителей и др. Заметим, что фиктивные работы (зависимости) показывают, что одна работа предваряет другую (на графике изображаются пунктиром). Крупный проект разбивается на отдельные операции, составляется перечень и последовательность их выполнения, планируется время выполнения. Данные собираются в структурно-временную таблицу:

Правила построения сетевого графика:

- «тупиком» может быть только завершающее событие;

- все события проекта, кроме исходного, имеют предшествующие события;

- запрещено наличие циклов;

- при изображении параллельно выполняемых работ необходимо использовать фиктивные работы, чтобы два смежных события не были связаны двумя или большим количеством дуг.

На сетевом графике события изображаются геометрическими фигурами (круги, квадраты), в каждой указывают:

- номер вершины i, присвоенный согласно алгоритму правильной нумерации;

- T_i^р – ранний срок наступления i-го события;

- T_i^п – поздний срок наступления i-го события;

- k – номер вершины, при движении из которой получено значение T_i^р.

Алгоритм правильной нумерации вершин (номера концевых вершин меньше номеров начальных вершин для всех дуг).

1. Пронумеровать начальную вершину. Вычеркнуть все дуги, выходящие из пронумерованной вершины.

2. Если достигнута конечная вершина, то процесс завершен. В противном случае, перейти к п.1.

Алгоритм поиска раннего срока наступления i-го события.

1. T₁^р:=0.

2. T_i^р:= max_k { T_k^р+t_ki}, где (k,i) – дуги, входящие в i-ю вершину, .

Алгоритм поиска позднего срока наступления i-го события.

1. T_n^п:= T_n^р .

2. T_i^п:= min_k { T_k^п - t_ki}, где (i,k) – дуги, выходящие из i-й вершины, .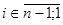

Алгоритм построения критического пути.

1. Начинают построение из конечной вершины в вершину с номером К, при движении из которой получено значение T_i^р. Если в какой-то вершине находится два номера, то путь раздваивается.

2. Процесс продолжают пока не дойдут до начальной.

При анализе сетевого графика используют временные параметры:

- ранний срок начала работы (i,j) t_ij ^рн– наименьшее допустимое время, когда работа может быть начата: t_ij ^рн= T_i^р;

- ранний срок окончания работы (i,j) t_ij ^ро = t_ij ^рн ₊ t_ij ;

- поздний срок окончания работы (i,j) t_ij ^рн– наибольшее допустимое время, когда работа может быть окончена без нарушения срока завершения всего проекта: t_ij ^по= T_j^п;

- поздний срок начала работы (i,j) t_ij ^пн = t_ij ^по - t_ij;

- критическое время T_кр – ранний срок наступления конечного события, минимальный срок выполнения всего комплекса работ;

- полный резерв времени работы (i,j) – максимально допустимое время, на которое можно увеличить продолжительность выполнения работы (i,j) или отложить ее начало, не вызвав при этом задержки выполнения всего проекта:

R_ij=T_j^п – T_i^р- t_ij;

- свободный резерв времени работы (i,j) – время, которое можно дополнительно выделить для выполнения работы (i,j) без влияния на время выполнения последующих работ, причем последующие работы могут быть начаты в свои ранние сроки: r_ij=T_j^р – T_i^р- t_ij;

- коэффициент напряженности , где t^’_кр – продолжительность отрезка рассматриваемого пути, совпадающего с критическим. Если К_н>0,8, то работы напряженные, если 0,6<К_н<0,8, то работы подкритические, если К_н<0,6, то работы с резервами, при К_н = 1 работы напряженные.

Иногда продолжительности работ трудно задать точно, тогда вместо одной детерминированной оценки задается две оценки: минимальная (оптимистичный прогноз времени выполнения) и максимальная (пессимистичный прогноз времени выполнения), и принимается, что t_ij – случайная величина, подчиняющаяся b-распределению, т.е. t_ij=(3t_max - 2 t_min)/5, с дисперсией s²=0,04(t ²_max - t ²_min), тогда вероятность p(t_кр<T)=0,5(1+Ф(z)), где z=(T- t_кр)/ s_кр ; Т – директивный уровень продолжительности выполнения всего проекта. Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности p вычисляется по формуле: T=T_кр+zs_кр, где s_кр= , D- дисперсия продолжительности критического пути, , где s_ij² – дисперсии работ критического пути.

Часто необходимо улучшить параметры сетевого графика, т.е. требуется оптимизация использования материальных, временных и трудовых ресурсов. Рассмотрим оптимизационные задачи сетевого планирования.

1 Оптимизация по времени. Пусть задан сетевой график выполнения проекта, известны d_ij – показатели минимально возможного времени выполнения работы (i,j) и h_ij - технологические коэффициенты использования дополнительных средств x_ij, позволяющих сократить длительность выполнения работы (i,j) до величины t^’_ij = t_ij - h_ij x_ij . Задача 1 состоит в нахождении величин x_ij с целью минимизации суммарных дополнительных расходов и в нахождении времени начала t_ij ^н и окончания t_ij ^о работ (i,j), чтобы проект был выполнен в срок t₀. Математическая модель задачи имеет вид: F= →min

при условиях:

,

,

,

,

Задача 2 состоит в нахождении величин x_ij с целью сокращения срока выполнения проекта и нахождения времени начала t_ij ^н и окончания t_ij ^о работ (i,j), чтобы сумма дополнительных расходов не превышала величины B. Математическая модель задачи имеет вид:

при условиях:

,

,

,

2 Оптимизация по стоимости выполнения работ (прямых затрат).

Пусть задан сетевой график выполнения проекта, известны d_ij – показатели минимально возможного времени выполнения работы (i,j) (срочный режим выполнения), которым соответствуют наибольшие затраты С_ij, и D_ij – показатели максимально возможного времени выполнения работы (i,j) (нормальный режим выполнения), которым соответствуют наименьшие затраты c_ij (предполагается, что затраты на выполнение работ обратно пропорциональны времени их выполнения). h_ij = - коэффициенты дополнительных затрат (КДЗ).

1 случай (длина критического пути не фиксирована). Если все работы выполняются в нормальном режиме, то критический срок будет наибольшим, а стоимость выполнения наименьшей, поэтому необходимо сократить критический срок до некоторого минимально возможного значения при наименьшем возрастании стоимости выполнения проекта.

Алгоритм решения задачи.

Предварительный шаг. Определить КДЗ h_ij. На основе D_ij определить T_кр , R_ij, затраты на реализацию всего комплекса работ С.

Общий шаг.

1. Среди критических работ найти работу (r,k), для которой КДЗ наименьший. Если работа (r,k) является общей для всех критических путей или этот путь один, то работа (r,k) подлежит сокращению. Если работа (r,k) не является для критических путей общей, но эти пути имеют одну или несколько общих работ, то на каждом из них найти работу с наименьшим КДЗ и суммировать их. Сравнить с КДЗ той из общих работ (l,s), для которой он наименьший. Если суммарная величина КДЗ окажется не больше h _l,s , то все работы, КДЗ которых вошли в сумму подлежат сокращению, в противном случае, сокращению подлежит работа (l,s). Если критические пути не имеют общих работ, то на каждом из них найти работу, для которой КДЗ наименьший, которая подлежит сокращению.

2. Сократить продолжительность выбранной работы, на такую величину, чтобы показатель времени выполнения работы (i,j) достиг значения d_ij или образовался новый критический путь.

3. Определить T_кр , R_ij, затраты на реализацию нового варианта сетевого графика С.

4. Проверить, все ли работы критического пути достигли минимальной продолжительности, в этом случае задача решена. В противном случае перейти к п.1.

2 случай (длина критического пути фиксирована величиной t₀). Задача состоит с минимизации стоимости выполнения проекта за счет увеличения длительности выполнения некоторых работ, но с учетом условия T_кр≤ t₀. Если T_кр= t₀, то оптимизация возможна только за счет резервов некритических работ. Если T_кр<t₀, то оптимизация возможна только за счет всех работ проекта, все работы станут критическими (план безрезервный).

Будем считать неизвестными сроки t_i свершения событий, тогда в оптимальном плане длительность работы t_ij=t_j-t_i, а ее стоимость . Математическая модель задачи имеет вид:

3 Оптимизация по ресурсам. Пусть проект задан сетевым графиком и используется один вид ресурсов в количестве R. Каждая работа характеризуется продолжительностью выполнения t_ij и интенсивностью потребления ресурса r_ij. Оптимальным распределением ресурсов считается такое размещение работ во времени, при котором в каждый момент времени было бы достаточно ресурс для выполнения работ, а время выполнения всего комплекса было бы минимальным, и работы не допускают перерыва в выполнении. Для решения этой задачи широко используют эвристические методы.

Алгоритм

Предварительный шаг. Составляют линейный график выполнения проекта (график Ганта), на котором каждая работа (i;j) изображена в привязке к оси времени горизонтальным отрезком длины t_ij, начало работы T_i^р . Находят T_кр.

Первый шаг.

1. Проецируем на ось времени начало и конец каждой работы, пронумеруем эти проекции, начиная с нуля.

2. Определяем полные резервы времени работ, расположенных над промежутком (0;1). Нумеруем эти работы в порядке возрастания полных резервов. Если полные резервы одинаковы, то нумеруем эти работы в порядке убывания интенсивностей потребления ресурса.

3. Суммируем последовательно интенсивности потребления ресурса работ, расположенных над промежутком (0;1), в порядке присвоенных им номеров и сравниваем полученные суммы с R. Все работы, для которых сумма интенсивностей меньше либо равна R, оставляем в первоначальном положении, как только сумма станет превышать R, то эту работу сдвигаем вправо на величину рассматриваемого промежутка, переходим к следующей работе, пока не будут просмотрены все работы, расположенные над промежутком (0;1).

4. Результатом выполнения этого шага является новый линейный график.

Общий шаг. Пусть выполнено k шагов алгоритма, и получен новый линейный график, k-ый момент является началом оставшейся части комплекса работ.

1. Проецируем на ось времени начало и конец каждой работы, пронумеруем эти проекции, начиная с k-1 .

2. Определяем полные резервы времени работ, расположенных над промежутком (k-1; k). Нумеруем эти работы в порядке возрастания полных резервов. Если полные резервы одинаковы, то нумеруем эти работы в порядке убывания интенсивностей потребления ресурса.

3. Суммируем последовательно интенсивности потребления ресурса работ, расположенных над промежутком (k-1; k), в порядке присвоенных им номеров и сравниваем полученные суммы с R. Все работы, для которых сумма интенсивностей меньше либо равна R, оставляем в первоначальном положении, как только сумма станет превышать R, то эту работу сдвигаем вправо на величину рассматриваемого промежутка, переходим к следующей работе, пока не будут просмотрены все работы, расположенные над промежутком (k-1; k).

4.Результатом выполнения этого шага является новый линейный график.

5. Проверяем, все ли работы комплекса просмотрены. Если да, то решение закончено, в противном случае возвращаемся к п.1 общего шага. [21, 28]