Билет № 1.

$$$ 247

функциясы берілген. нүктесіндегі дербес туындыларының қосындысының мәні:

$$$ 248

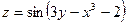функциясы берілген. нүктесіндегі дербес туындыларының қосындысының мәні:

$$$ 249

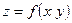функциясының толық дифференциалының формуласын көрсетіңіз:

$$$ 250

Төменде көрсетілген формулалардың ішінде қайсысы екі айнымалы функцияның градиентін көрсетеді

$$$ 251

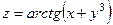функциясы берілген. нүктесіндегі дербес туындыларының қосындысының мәні:

$$$ 252

функциясының нүктесіндегі градиентінің координаттарын тап

$$$ 253

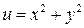функциясының нүктесіндегі градиентінің координаттарын тап

$$$ 254

функциясының нүктесіндегі градиентінің координаттарын тап

$$$ 255

функциясының нүктесіндегі градиентінің координаттарын тап

$$$ 256

функциясы экстремум немесе стационар нүктелерінде қандай шартты қанағаттандырады

$$$ 257

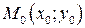функциясының нүктесінде аргументі бойынша алынған дербес туындысын көрсет

$$$ 258

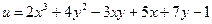функциясының 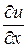- дербес туындысын тап

$$$ 259

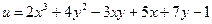функциясының - дербес туындысын тап

$$$ 260

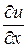функциясының - дербес туындысының нүктесіндегі мәнін тап

$$$ 261

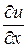функциясының - дербес туындысының нүктесіндегі мәнін тап:

$$$ 262

функциясының - дербес туындысының нүктесіндегі мәнін тап:

$$$ 263

функциясының - дербес туындысының нүктесіндегі мәнін тап:

$$$ 264

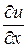функциясының - дербес туындысының нүктесіндегі мәнін тап:

$$$ 265

функциясының - дербес туындысының нүктесіндегі мәнін тап:

$$$ 266

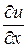функциясының - дербес туындысының нүктесіндегі мәнін тап:

$$$ 267

функциясының - дербес туындысының нүктесіндегі мәнін тап:

$$$ 268

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

$$$ 269

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

$$$ 270

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

$$$ 271

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап:

$$$ 272

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап

$$$ 273

функциясының - екінші ретті дербес туындысының нүктесіндегі мәнін тап

$$$ 274

функциясының - екінші ретті аралас туындысының нүктесіндегі мәнін тап

$$$ 275

функциясының толық дифференциалын табыңыз

$$$ 276

функциясының толық дифференциалын көрсет

$$$ 277

функциясының толық дифференциалын тап

$$$ 278

функциясының толық дифференциалын тап

$$$ 279

Екі айнымалыдан тәуелді функциясы айқындалмаған түрде берілсе, яғни , онда шартын қанағаттандыратын функциясының х бойынша бірінші ретті дербес туындысын тап

$$$ 280

функциясының - дербес туындысын тап

$$$ 281

функциясының - дербес туындысын тап:

$$$ 282

функциясының - дербес туындысын тап:

$$$ 283

функциясының - дербес туындысын тап

$$$ 284

функциясының - дербес туындысын тап

$$$ 285

функциясының - дербес туындысын тап:

$$$ 286

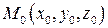бетінде жататын нүктесі арқылы жүргізілген жанама жазықтықтың теңдеуін көрсет:

$$$ 287

бетіне 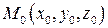нүктесі арқылы жүргізілген нормаль түзудің теңдеуін көрсет:

$$$ 288

Екі айнымалы функциясының нүктесінде экстремум болуының қажетті шартын көрсет:

$$$ 289

функциясының нүктесінде векторының бағыты бойынша алынған туындысын тап

$$$ 290

функциясының нүктесінде векторының бағыты бойынша алынған туындысын тап

Билет № 1.

Механика – наука о движении и равновесии тел. При построении теории физика заменяет реальные обьекты их идеализированными моделями. Движение – это изменение относительнеого положения тела с течением времени. Впервые принципы механики сформулированы Ньютоном в «Математических началах натуральной философии».

Тело или система тел, относительно которых определяется положение остальных тел называется простанственной системой отсчета (ПСО). В качестве ПСО можно взять произвольное твердое тело и связать с ним координатные оси, например, декартовой системы координат. Существует два вида координатных систем: 1) правая, 2) левая. Определяются они с помощью правила буравчика.

Пространство (по Ньютону) – это совокупность физического тела и возможных его продолжений.

Время – это показание каких-то часов (под часами понимается любое тело или система тел, в которых совершается периодический процесс, служащий для измерения времени).

Кинематика занимается изучением движение тела не абстрагируясь на его причины.

Движение материальной точки будет описано полностью, если известно ее положение в любой момент времени относительно выбранной системы отсчета. Полное описание движения сводится к нахождению трех координат: x = x(t); y = y(t); z = z(t); или к нахождению векторной функции r = r(t). . – мгновенная скорость. Производная скорости по времени называется ускорением материальной точки: ,

Уравнение кинематической связи –уравнение связывающее кинематические характеристики тел системы.

Закнон движения – это зависимость координат точки от времени. Закон движения можно рассматривать как уравнение траектории где t параметр.(уравнение траектории – уравнение кривой по которой движется точка.)

Материальная точка – это тело, размеры которого пренебрежимо малы, что в рассматриваемом движении их можно не принимать во внимание и считать, что все вещество тела как бы сосредоточено в одной точке. Материальная точка – это абстракция, идеализированный образ реально существующих тел.

Система мат. Точек – некоторая совокупность их числа.

Пункт 2.

Гироскоп – массивное аксиально-симметричное тело, вращающееся с большой угловой скоростью вокруг оси симметрии.

Гироскопическая сила – сила, действующая на опору со стороны быстро вращающихся масс.

Если гироскоп раскручен вокруг оси симметрии, то L=Jw=const и направление оси симметрии остаётся неизменным. Прецессия гироскопа.(к оси гир. приложена сила, линия действия которой не проходит через точку закрепления).

Ось гироскопа перемещается не в направлении сил, а перпендикулярно к ней. Элементарная теория гир.(мгн. угловая скорость вращения и мом. импульса направлены вдоль оси симметрии, w>>W). Мом. импульса: L=J_zw (J_z – мом. ин. относительно оси симметрии) Рассмотрим гир, у которого точка опоры S не совпадает с центром масс О. Мом силы тяжести: M=mglsinq, где q - угол между вертикалью и осью симметрии. dL=M*dt, при этом и ось и L прецессируют вокруг вертикали с угл скоростью W. dL=L sinq W dt dL= WxL dt M=WxL Для силы тяжести: mgl sinq = WJ_zw sinq угл скорость прецессии W=mgl/ J_zw. Если сообщить гироскопу толчок, изменяющий угол q , то прецессия перестанет быть равномерной (часто говорят: регулярной), а будет сопровождаться мелкими колебаниями вершины гироскопа – нутациями. Вектор момента импульса L описывает неподвижный в пространстве конус прецессии, и при этом ось симметрии гороскопа движется вокруг вектора L по поверхности конуса нутации. Вершина конуса нутации, как и вершина конуса прецессии, находится в точке закрепления гироскопа, а ось конуса нутации совпадает по направлению с L и движется вместе с ним. Угловая скорость нутации определяется выражением w_нут=L/J_s@J_zw/J_s где J_z и J_s - моменты инерции гироскопа относительно его оси симметрии и относительно оси, проходящей через точку опоры и перпендикулярной оси симметрии, w - угловая скорость вращения вокруг оси симметрии. Раскрутим гироскоп вокруг его оси симметрии до большой угловой скорости (момент импульса L) и станем поворачивать раму с укрепленным в ней гироскопом вокруг вертикальной оси с некоторой угловой скоростью W. Момент импульса L получит при этом приращение dL, которое должно быть обеспечено моментом сил М, приложенных к оси гироскопа. Момент М, в свою очередь, создан парой сил F+ F`, возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами Ф + Ф`. Эти силы называются гироскопическими, они создают гироскопический момент М` . Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса.

Гироскопический момент нетрудно рассчитать. Положим, согласно элементарной теории, что L=Jw Где J – момент инерции гироскопа относительно его оси симметрии, а w - угловая скорость собственного вращения. Тогда момент внешних сил, действующих на ось, будет равен M=WxL=Wx(Jw) Где W – угловая скорость вынужденного поворота ( иногда говорят: вынужденной прецессии).Со стороны оси на подшипники действует противоположный момент M`=-M= (Jw)xW Направление гироскопических сил можно найти легко найти с помощью правилa, сформулированного Н.Е.Жуковским гироскопические силы стремятся совместить момент импульса L гироскопа с направлением угловой скорости вынужденного поворота.