Пункт 2. По мере увеличения высоты давление и плотность монотонно убывают, а температура монотонно убывает лишь в нижнем десятикилометровом слое

По мере увеличения высоты давление и плотность монотонно убывают, а температура монотонно убывает лишь в нижнем десятикилометровом слое, а в более высоких слоях меняется немонотонно. Параметры атмосферы зависят как от географического положения места, так и от времени года. Сложная высотная зависимость температуры атмосферы есть результат совместного проявления процессов тепломассопереноса, инициируемых излучением Солнца.

Атмосфера делится на отдельные участки. Нижний слой атмосферы,называемый тропосферой,содержит 80% массы атмосферы, почти весь водяной пар и облака и характеризуется сильным вертикальным перемешиванием. Сверху тропосфера ограничена тропопаузой, где температура меняется очень мало. Выше расположена стратосфера,где температура повышается, и заканчивает повышаться в стратопаузе. Выше находится мезосфера, где температура опять падает. Выше находится термосфера, в которой температура опять растет до 600-2000 К. Для вычисления изменения атмосферного давления с высотой воспользуемся условием равновесия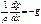

Связь между давлением и плотностью задается уравнением состояния идеального газа , т. к. влияние влажности на плотность воздуха сущ. лишь в тропиках на поверхности и ошибка <2%.

Получаем ур-ие .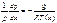

Которое можно проинтегрировать, если известно Т(х).

В качестве грубого приближения можно использовать среднее значение температуры 250 К.

Интегрируя получим барометрическую ф-лу: .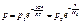

По этому же закону изменяется и плотность воздуха: .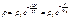

Приведенная высота (высота на которой давление падает в е раз): .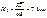

Билет № 6.

Назовем импульсом или количеством движения материальной точки вектор, равный произведению массы точки на ее скорость: Р=m×v

Импульсом или количеством движения системы материальных точек назовем векторную сумму импульсов отдельных материальных точек, из которых эта система состоит.

Произведение постоянной силы F на время ее действия называется Импульсом силыза то же время.

Закон сохранения импульса.Импульс изолированной или замкнутой системы 2-х материальных точек сохраняется, т. е. остается неизменным во времени, каково бы ни было взаимодействие между ними. Это утверждение справедливо также и для изолированной с. м. т., состоящей из сколь угодно большого числа м. т.

Запишем третий закон Ньютона для замкнутой системы, состоящей из произвольного числа материальных точек.

F₁⁽ⁱ⁾+F₂⁽ⁱ⁾+…+Fn⁽ⁱ⁾=0, (1)

где Fn⁽ⁱ⁾ – полная внутренняя сила., действующая на n-ную точку. Обозначим далее символами F₁^(e),F₂^(e),… внешние силы , действующие на материальные точки системы. Тогда на основании второго закона Ньютона можно записать

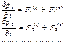
Сложив почленно эти уравнения и приняв во внимание соотношение (1) найдем

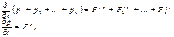(2)

где р- импульс всей системы,F^(e)-равнодействующая всех внешних сил, действующая на нее. Пусть теперь геометрическая сумма всех внешних сил равна нулю (Например, замкнутая система). Тогда (dp/dt)=0, или p=const.

Закон сохранения импульса является отражением фундаментального св-ва пространства - его однородности.

Изолированная система – система тел, настолько удаленных от всех остальных тел, что они практически не оказывают действия на рассматриваемую систему.

Замкнутая система – это система, удалённая от остальных тел, на которую не оказывается действие.

Пункт 2. На тела, погруженные в жидкость, действует выталкивающая сила, направленная вертикально вверх. Эта сила является результатом действия сил давления. Выталкивающая сила F_А, называемая силой Архимеда,может быть подсчитана при учете распределения давления по глубине и оказывается равной весу вытесненной жидкости. Извлечём из сосуда с жидкостью тело, затем дольём туда жидкости (той же). Выделим мысленно границы тела в жидкости и поймём, что сумма действ. сил на жидкость внутри условных границ =0 Þ Архимедова сила равна весу вытесненной жидкости. Центр масс погруженного тела может не совпадать с центром объема. Это несовпадение имеет большое значение для устойчивого плавания тел, погруженных в жидкость (в кораблестроении используется термин остойчивость).

Для тел, плавающих на поверхности жидкости, центр их тяжести всегда будет расположен выше центра объема, погруженного в жидкость, и остойчивость плавания достигается выбором подобающей формы корабля и его загрузки. В судостроении форму судна с учетом его загрузки рассчитывают таким образом, чтобы метацентр находился выше центра масс судна . Этот метацентр является центром кривизны кривой , проходящий через центры объемов погруженных частей корпуса корабля.,сменяющих друг друга при его боковой качке.