Билет № 7.

В нерелятивистской механики импульс системы р может быть выражен через скорость ее центра масс. Центром масс или центром инерции системы называется такая воображаемая точка, радиус-вектор R которой выражается через радиусы-векторы r₁,r₂,… материальных точек по формуле

R=(m₁r₁+m₂r₂+…)/m , где m=m₁+m₂+… .Если продифф. Выражение по времени и умножить на m то получится: 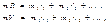, 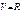-скорость центра масс системы. Таким образом, p=mV. Подставив это в (2): 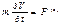Центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила - геометрической сумме всех внешних сил, действующих на систему. В релятивистском случае потятие ц. м. не является инвариантным понятием, не зависящем от выбора системы координат, и поэтому не применяется. Для материальной точки з. с. импульса означает, что в отсутствии внешних сил она движется с постоянной скоростью по прямой линии. Для СМТ в нерелятивистском случае закон утверждает, что ц. м. движется равномерно и прямолинейно.

Под однородностью пространства понимается эквивалентность всех точек пространства друг другу. Это означает, что если имеется некоторая изолированная система, то развитие в ней не зависит от того, в точках какой области пространства эта система локализована. Если все точки системы сместить на Dr, то в состоянии системы ничего не изменится, т. е. работа внутренних сил системы =0. Dr Ввиду независимости взаимодействий каждой из пар точек друг с другом Þ F_ij+F_ji=0. Þ закон созранения импульса изолированной системы материальных точек обусловлен фундаментальным свойством пространства в ИСО –– его однородности. Отсюда можно заключить, что с однородностью пространства связан и принцип относительности.

Пункт 2. Рассмотрим стационарное течение жидкости в каком-либо консервативном силовом поле, например, в поле силе тяжести. Применим к этому течению закон сохранения энергии. При этом полностью пренебрегаем теплообменом между жидкостью и средой. Выделим в жидкости бесконечно узкую трубку тока и рассмотрим часть жидкости, занимающую объём MNDC. Пусть эта часть переместилась в бесконечно близкое положение M₁N₁D₁C₁. Вычислим работу А, совершаемую при этом силами давления. Давление, действующее на боковую поверхность трубки тока, перпендикулярно к перемещению и работы не совершает. При перемещении границы MN в положение M₁N₁ совершается работа А₁=P₁S₁L₁, где L₁=MM₁- величина перемещения. Введя объём D₁V=S₁L₁,ее можно представить в виде А₁=P₁DV₁ или А₁=P(D₁m/r₁), где D₁m- масса жидкости в объеме MNN₁M₁. При перемещении границы CD в положение границы C₁D₁ жидкость совершает работу против давления P₂. Для нее, рассуждая аналогично, найдём А₂ =P₂(D₂m)/r₂ , где D₂m- масса жидкости в объеме CDD₁C₁. Но если движение стационарно, то масса жидкости в объеме M₁N₁DC не изменится, следовательно D₁m=D₂m=Dm, получим А=А₁-А₂=(P₁/r₁ -P₂/r₂) Dm. Эта работа = приращению DЕ полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M₁N₁DC не изменилась. Поэтому величина DE= разности энергий массы жидкости Dm, в положениях CDD₁C₁ и MNN₁M₁. Находим DЕ=(e₂-e₁)Dm, где e - полная энергия, приходящаяся на единицу массы жидкости. Приравняв DE к А и сократив на Dm получим: e₁+P₁/ =e₂ +P₂/r₂ . Отсюда следует, что вдоль одной и той же линии тока при стационарном течении идеальной жидкости величина e+P/r остаётся постоянной: e+P/r=B=const-это отношение называется уравнением Бернулли. Оно справедливо и для сжимаемых жидкостей. Требуется только, чтобы жидкость была идеальной, а течение- стационарным.

Линия, касательная которой указывает направление скорости частицы жидкости, проходящей в рассматриваемый момент времени через точку касания, называется линией тока. Если поле скоростей, а следовательно, соответствующие ему линии тока не меняются с течением времени, то движ. жидкости называется стационарным или установившемся.

Возьмем произвольный замкнутый контур С и через каждую точку его в один и тот же момент времени проведём линии тока. Они расположатся на некоторой трубчатой поверхности, называемой трубкой тока.Так как скорости частиц жидкости направлены по касательным к линиям тока, то при течении жидкость не может пересекать боковую поверхность трубки тока. Масса жидкости, протекающая за время dt через попер. сечение трубки будет: dm=rvSdt. Если взять 2^А сечения S₁=S₂, то: r₁v₁S₁=r₂v₂S₂, если жидкость не сжимаема, то r₁=r₂ получится: (v₁/v₂)=(S₂/S₁). Скорость жидкости в одной и той же трубке тока тем больше, чем уже поперечное сечение трубки.

Билет № 8.

Уравнение движения тел с переменной не содержат ничего принципиально нового по сравнению с законами Ньютона, и являются их следствиями. Но они представляют большой интерес в связи с ракетной техникой.

Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Пусть m(t)-масса пакеты в произвольный момент времени t, а v(t)-ее скорость в тот же момент. Импульс ракеты в этот момент будет mv. Спустя dt масса и скорость ракеты получат приращение dm и dv( dm-отрицательна). Импульс ракеты станет (m+dm)(v+dv). Сюда надо добавить импульс движения газов, образовавшихся за dt. Он равен dm_газv_газ –масса и скорость газа, образовавшихся за dt. Вычитая из суммарного импульса системы в момент t+dt импульс системы в момент t, найдем приращение этой величины за dt. Это приращение равно Fdt, где F – геометрическая сумма всех внешних сил, действующих на ракету. (m+dm)(v+dv)+dm­_газv_газ-mv = Fdt Время dt устремим к нулю. Поэтому, раскрывая скобки, отбрасываем dmdv. Далее dm+dm_газ=0 и v_отн=v_газ-v есть скорость истечения газов относительно ракеты. Тогда mdv = v_отнdm + Fdt , деля на dt m(dv/dt) =v_отн(dm/dt) + F (1)

Член v_отн(dm/dt) – реактивная сила . Уравнение (1)-уравнение Мещерского или уравнение движения точки с переменной массой.

Пусть теперь у нас F=0, тогда mdv = v_отнdm. Допустим, что ракета движется прямолинейно в направлении, противоположном скорости v_отн. Тогда проекция v_отн на направление движения будет –v_отн. Тогда dv/dm = -(v_отн/m) Пусть скорость газовой струи v_отн постоянна, тогда v= - v_отн ò(dm/m) = - v_отн ln(m) + C Значение С определяется начальными условиями. Если, в начальный момент времени скорость ракеты =0, а масса = m_0, тогда 0 = - v_отн­ ln(m₀) + C , откуда С = v_отн ln(m₀). Следовательно : v = v_отн ln(m/m₀) или m₀/m=e^{v / v отн} .(2)

Уравнение (2) – формула Циолковского. Она справедлива для нерелятивистских движений (v и v_отн­ << c ) Релятивистская формула имеет вид : , где b= v/c .

Пункт 2.

Билет № 9.

Пункт 1. Смотри предыдущий билет.

Пункт 2.

Силы вязкого трения. Ньютон установил опытным путем, что при скольжении друг относительно друга двух параллельных плоскостей, пространство между которыми заполнено жидкостью, силы вязкого трения препятствуют этому скольжению (рис. 4.1). Эта сила пропорциональна площади S и изменению скорости на единицу длины в поперечном направлении h/v (градиенту скорости в направлении, перпендикулярном движению) и зависит также от вязкости жидкости m:. F=mSv/h. h²<<S. Важно отметить, что частицы жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней (неподвижной) пластины находятся в покое (прилипают к пластине). Представим, что жидкость между пластинами состоит из плоских параллельных слоев, движущихся равномерно (рис. 4.2). Нетрудно понять, что каждый вышележащий слой увлекает за собой нижний соседний слой с силой F. В свою очередь, этот нижний слой тормозит движение верхнего слоя с той же силой. На каждый слой действуют сверху и снизу две равные, но противоположно направленные силы. Скорость слоев возрастает от нижнего слоя к верхнему линейно (рис. 4.2), а силы трения, действующие на каждый из слоев, одинаковы. Как результат, усилие приложенное к верхней пластине, передается на нижнюю пластину.

Течение вязкой жидкости.Уравнение Навье-Стокса.

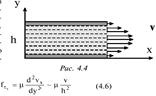
Для анализа течения вязкой жидкости в правую часть уравнения движения r(dv/dt)=F–drad p необходимо добавить силу вязкого трения, приложенную к единице объема жидкости. Для простоты ограничимся рассмотрением течения жидкости в направлении оси x, при это единственная компонента скорости vx будет зависеть от поперечной координаты y (рис. 4.3). На верхнюю грань dxdz кубика dxdydz (ось z перпендикулярна плоскости чертежа) в соответствии с F=(mSv/h) в направлении оси x действует увлекающая сила: , а на нижнюю грань тормозящая: 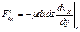. Равнодействующая сил вязкого трения, приложенная к выделенному кубику, равна F_t=F’_tx+F”_tx, a сила, приложенная к единичному объему, составит . В общем случае сила вязкого трения, вообще говоря, имеет три компоненты: f_t={f_tx, f_ty, f_tz}, где f_tx=mDv_x, f_ty=mDv_y, f_tz=mDv_z, где D= 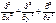— оператор Лапласа, для сокращения записи. Если теперь компоненты силы трения подставить в правые части уравнений:

для соответствующих компонент скоростей, то мы получим систему уравнений гидродинамики вязкой жидкости. Эти три уравнения могут быть записаны в виде одного векторного уравнения Навье-Стокса:

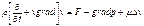
Течение вязкой жидкости по трубе. Формула Пуазейля.Если мы подсоединим тонкую горизонтальную стеклянную трубу с впаянными в нее вертикальными манометрическими трубками при помощи резинового шланга к водопроводному крану (рис. 4.6). При небольшой скорости течения хорошо видно понижение уровня воды в манометрических трубках в направлении течения (h 1 >h 2 >h 3 ). Это, в свою очередь, указывает на наличие градиента давления вдоль оси трубки — статическое давление в жидкости уменьшается по потоку. При равномерном прямолинейном течении жидкости силы давления уравновешиваются силами вязкости. Уравнение Навье-Стокса для этого случая запишется в виде:

-grad p+mDv=0. (4.12)

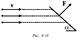
Распределение скоростей в поперечном сечении потока вязкой жидкости можно наблюдать при ее вытекании из вертикальной трубки через узкое отверстие (рис. 4.7). Если, например, при закрытом кране К налить вначале неподкрашенный глицерин, а затем сверху осторожно добавить подкрашенный, то в состоянии равновесия граница раздела Г будет горизонтальной. Если кран К открыть, то граница примет форму, похожую на параболоид вращения. Приравняем нулю сумму сил вязкости и давления, действующих на цилиндрический объем жидкости радиуса r и длиной dx (рис. 4.8): (p(x) – p(x+dx))pr²+m2prdx(dv/dr)=0(4.13)

Отметим, что равнодействующая сил давления направлена по потоку (вдоль оси x), а сила вязкого трения, приложенная к боковой поверхности выделенного цилиндра — против потока, поскольку dv/dr<0. Произведя сокращение и разделив (4.13) на dx, получаем:

–(dp/dx)+2mdv/(rdr)=0 (4.14)

Величина градиента давления dx/dp в (4.14) не зависит от радиуса r, т.к. давление p=p(x) и в поперечном сечении x=const не меняется. Это позволяет проинтегрировать (4.14):

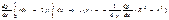(4.15)

Поток вектора скорости через поперечное сечение трубы, или объем жидкости, протекающей через сечение в единицу времени (на практике употребляют термин «расход жидкости») оказывается равным: .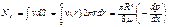

Для практических целей расход жидкости определяют по формуле Пуазейля: 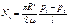Здесь расход воды N_v пропорционален разности давлений p₁– p₂ на длину.

Билет № 10.

Пункт 2.Число Рейнолдса также определяет относительную роль инерции и вязкости: при больших числах Рейнольдса более важна роль инерции, при малых – вязкости.Силы вязкости,возникающие в потоке, обратно пропорциональны квадрату характерного поперечного размера потока и пропорциональны скорости. Давления р₁ и р₂ по разные стороны изогнутой трубки тока будут разные. Возникающий градиент давления связан с ускореним частиц жидкости уравнением: r(dv/dt)@–grad p Для частицы: F_и–grad p+mDv=0 Þ силы вязкости значительно меньше сил инерции. В общем случае силы инерции обратно пропорциональны поперечному размеру потока и пропорциональны квадрату скорости. Re=rvh/m – число Рейнольдса, характеризующее отношение сил инерции к силам вязкости. Re>1 Þ жидкость можно рассматривать как невязкую.

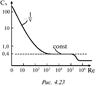
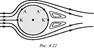
Тело в потоке вязкой жидкости. Лобовое сопротивление.Поток реальной жидкости или газа действует с некоторой силой на тело, помещенное в этот поток. Для осесимметричного тела с осью симметрии, направленной вдоль потока, эта сила также будет направлена вдоль потока. Она получила название силы лобового сопротивления.Основные физические причины возникновения лобового сопротивления можно установить наиболее просто, если рассмотреть обтекание потоком шара радиуса r. На рис. 4.21. изображена зависимость силы лобового сопротивления от числа Рейнольдса. При малых скоростях течения, когда Re<10² F_||~v, т. к. на шар действуют силы вязкости, возникающие вследствие существования тонкого пограничного слоя вблизи поверхности шара (d@r/(Re)^1/2). При таких скоростях происходит ламинарное (слоистое) течение жидкости. Вне этого слоя реальная жидкость течет так же, как и идеальная, обтекая шар симметрично. Наоборот, при числах Re ~ 1 говорить о пограничном слое некорректно, т.к. градиенты скорости существенны в области, размеры которой значительно больше радиуса шара. При малых числах Рейнольдса сила лобового сопротивления для шара подчиняется закону Стокса: F_||=6pmrv. При Re>10², симметрия обтекания нарушается — позади шара происходит отрыв линий тока (рис. 4.22). При таких скоростях пограничный слой становится очень тонким, а поперечные градиенты скорости в нем — большими. Силы вязкости, которые при этом возрастают, тормозят движение частиц среды, движущихся вдоль поверхности шара, настолько, что они не в состоянии полностью обогнуть шар. Хотя течение в тонком пограничном слое остается ламинарным, позади шара образуются вихри. Симметрия давлений в точках А и A’ нарушается. F_||=C_X Srv²/2, где C_X — коэффициент лобового сопротивления для тела данной формы. Область квадратичной зависимости силы F от скорости v простирается вплоть до чисел Рейнольдса Re~10⁵. При больших скоростях пограничный слой постепенно турбулизуется, и при Re=3 10⁵ он полностью турбулентен. Для ламинарного и турбулентного обтекания тел можно использовать единую формулу для расчета силы лобового сопротивления: F_||=C_X(Re)Srv²/2, в которой коэффициент лобового сопротивления должен зависеть от скорости так, как это изображено на рис. 4.23.

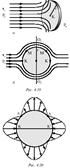
Взаимодействие тела с потоком идеальной жидкости.Еще Ньютоном была сформулирована получившая название ударной теория, базирующаяся на представлении воздуха в виде отдельных не связанных друг с другом материальных частиц. Согласно этой теории сила давления воздушного потока на площадку S, наклоненную под углом a (углом атаки) к направлению потока, равна: F=rSv²sin²a. Эта формула легко получается, если подсчитать импульс неупругих ударов составляющих ее материальных частиц. Опытная проверка этой формулы показала, что она неверно описывает зависимость силы F от угла атаки. И только при скоростях потока, значительно больших скорости звука, формула Ньютона оказывается справедливой. Модель воздуха как совокупности дискретных частиц является неверной. Реальные же силы могут быть подсчитаны на основе гидродинамического подхода, учитывающего обтекание тела движущимся потоком континуальной среды. Пусть в движущемся со скоростью v₀ потоке помещены диск и шар одинакового радиуса r (рис. 4.19). В центре диска точке K, называемой критической, поток останавливается (v = 0), и давление, согласно уравнению Бернули, равно: p_k=p₀+(rv₀²/2). Из-за поворота трубок тока на 90⁰ давление в других точках на поверхности диска будет таким же, как и в точке К. Поэтому, если позади диска давление равно p₀ , то поток действует на диск с силой F_||=(p_k–p₀)pr²=rv₀²S/2. Гидродинамическая сила F , которая может трактоваться как сила лобового сопротивления при движении диска со скоростью v0 в потоке, вдвое меньше силы, вычисляемой на основе ударной теории ((1) при sin a=1). Если теперь в поток поместить шар, то по ударной теории на него будет действовать та же сила, что и на диск. При гидродинамическом подходе эта сила будет отсутствовать вовсе. Действительно, при симметричном потоке относительно сечения О₁ О₂ давления в произвольной точке М и симметричной точке M' будут одинаковы, поскольку одинаковы скорости потока в этих точках. Равенство нулю результирующей силы при плавном (безотрывном) обтекании идеальной жидкостью шара, цилиндра и другие. называется парадоксом Даламбера. Давление в любой точке потока вблизи поверхности шара можно рассчитать, пользуясь уравнением Бернулли: p_k=p₀+(rv₀²/2)–(rv²/2). На рис. 4.20 изображено распределение избыточных сил давления s_p=p–p₀, действующих по нормали к поверхности шара. Отсутствие сил в точках А и Aґ есть результат равенства скоростей в этих точках исходной скорости потока. При больших числах Рейнолдса сила лобового сопротивления обусловлена разностью давлений, а при малых – вязкостью.

Пункт 1. Момент импульса материальной точки.Пусть положение некоторой материальной тоски относительно точки О, принятой за начало координат, характеризуется радиусом-вектором r. Моментом импусльса материальной точки относительно О называется вектор L=r´p.

Моментом импульса системы материальных точек относительно тоски О , принятой за начало, называется сумма моментов импульса, материальных точек, составляющих систему.

Моментом силы F относительно точки O называется векторное произведение радиус-вектора r на силу F: M=[rF].

Момент силы относительно оси есть проекция на эту ось его момента относительно точки лежащей на той же оси.

Закон сохранения момента импульса.Этот закон справедлив лишь для изолированных систем. Для них момент внешних сил М равен нулю и уравнение моментов принимает вид dL/dt=0

Интегрируя это уравнение получаем L=const, L_x=const, _y=const, L_z=constЭто равенство выразает закон сохранения момента импульса:момент импусльса изолированной системы не изменяется при любых процессах, происходящих внутри системы. Может случится, что система не является полностью изолированной, но на некоторое направление, например на ось z, проекция момента сил равна нулю. Тогда уравнение моментов озапишится в проециях в следующем виде: dL_x/dt=M, dL_y/dt=M, dL_z/dt=0. L_z=const. Поэтому закон сохранения момента импульса можно применять не только к полностью изолированным системам, но и к частичнро изолированным.

Билет № 11.

Работой силы F на перемещении ds называется проэкция Fs на направление перемещения, умноженная на само перемещение: dA = Fds = F*ds*cosx , где x – угол между векторами F и ds. Величина dA называется элементарной работой. Энергия системы – это запас ее работы. Кинетическая энергия – запаса работы системы которую она может совершить двигаясь до полной остановки. Потенциальная энергия – запас той работы системы которую она может совершить изменением своей конфигурации (взаимного расположения своих частей).

Пункт 2.

Подъемная сила – перпендикулярная составляющая силы действующей на тело со стороны потока.

Если неподвижный круглый цилиндр обтекается равномерным потоком воздуха, перпендикулярным к его оси, то вследствие симметрии возникает только лобовое сопротивление, но никакой подъемной силы не появляется. Если однако цилиндра привести во вращение, то появляется подъемная сила перпендикулярная к направлению внешнего потока, и цилиндр отклоняется в сторону. Это явление называется эффектом Магнуса.

Билет № 12.

Консервативными наз. силы, зависящие только от конфигурации системы, и работа которых по любому замкнутому контуру равна 0. Все силы, не являющиеся консервативными, называются неконсервативными. К ним относятся прежде всего диссипативные силы. Диссипативными называются такие силы, полная работа которых при любых движениях в замкнутой системе всегда отрицательна. Примером может служить сила трения или силы сопротивления в жидких и газообразных средах.

Какое-либо произвольное положение системы условно примем за нулевое. Работа, совершаемая конс. силами при переходе системы из рассматриваемого положения в нулевое, называется потенциальной энергией системы в первом положении. Потенциальная энергия при фиксированном нулевом положении зависит только от координат материальных точек системы. Иными словами, потенциальная энергия системы U является функцией только ее координат. В системе с одними только конс. силами полная энергия остается неизменной. Могут происходить только превращения энергий, но полный запас измениться не может (закон сохр. энергии).

Пункт 2.

Колебания – это повторяющееся движение. Число степеней свободы – это число независимых величин, которые необходимо задать для того, чтобы однозначно определить положение тела в пространстве.

Колебания с одной степенью свободы – это колебания при которых движения системы можно описать одним независимым параметром (координатой). Пример: колебания математического маятника, колебания физического маятника (твёрдое тело, подвешенное за точку и способное колебаться вокруг оси, не проходящей через ц. м.), колебания груза на пружинке. Колебания происходящие по закону sinуса или cosинуса наз. гармоническими. Собственными называются колебания системы под действием лишь внутренних сил без внешних воздействий.

Уравнение собственных незатухающих колебаний: x’’+vx’=0. Его решение: x=Asin(wt+j) или x=Bcos(wt+j). Величина A называется амплитудой, w -частотой, wt+j -фазой, j - начальной фазой.

Билет № 13.

Абсолютно неупругим ударом, называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело.

Сталкивающиеся тела деформируются, возникают упругие силы и т.д. Однако если удар неупругий то, в конце концов все эти процессы прекращаются, и в дальнейшем оба тела, соединившись вместе, движутся как единое твёрдое тело.

v₁ v₂

m₁ m₂

Рассмотрим абс. неупругий удар на примере столкновения двух шаров. Пусть они движутся вдоль прямой, соединяющей их центры, со скоростями v₁ и v₂. В этом случае говорят что удар является центральным. Обозначим за V общую скорость шаров после соударения. Закон сохр. Импульса даёт:

m₁v₁+m₂v₂=(m₁+m₂)V Þ V=(m₁v₁+m₂v₂)/(m₁+m₂)

Кин. энергии системы до удара и после: K₁=1/2(m₁v₁²+m₂v₂²) K₂=1/2(m₁+m₂)V Пользуясь этими выраж. получаем: K₁-K₂=1/2m(v₁-v₂) ² где m =m₁m₂/(m₁+m₂) приведенная масса шаров. Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кин. энергии макроскопического движения, равная половине произведения приведённой массы на квадрат относительной скорости.

Абсолютно упругим ударомназывается столкновение тел, в результате которого их внутренние энергии не меняются. Пример: Столкновение бильярдных шаров из слоновой кости, при столкновениях атомных, ядерных частиц. Рассмотрим центральный удар двух шаров, движущ-ся навстречу друг другу:

(m₁v₁²)/2+(m₂ v₂²)/2=(m₁u₁²)/2+(m₂ u₂²)/2

и:

m₁v₁+m₂v₂=m₁u₁+m₂u₂

u1=[(m₁-m₂)v₁+2m₂v₂]/(m₁ +m₂)

u2=[(m₂-m₁)v₂+2m₁v₁]/(m₁+m₂)

При столкновении двух одинаковых абсолютно упругих шаров они просто обмениваются скоростями.

Пункт 2. см. предыдущий билет. Начальные условия: Гармоническое колебание полностью характеризуется частотой, амплитудой и начальной фазой.Частота зависит от физических свойств системы. Для определения амплитуды и начальной фазы колебаний надо знать положение и скорость материальной точки в некоторый момент времени.

Билет № 14.

Неинерциальные системы отсчёта (НИСО).НИСО называется система, движущаяся ускоренно относительно инерциальной. СО связана с телом отсчёта, которое, по определению, принимается за абсолютно твёрдое. Опр 2: в СО, в которых имеются силы тяготения и в к-х не выполняется 1-ый з-н Ньютона, наз. НИСО.

Описание движения мат. точки в НИСО.Чтобы описать движение в некоторой СО, необходимо разъяснить содержание высказывания о том, что такие-то события произошли в таких-то точках в такие-то моменты времени. Для этого надо, чтобы в СО $ единое время, но в НИСО единого времени в указанном §7 учебника Матвеева смысле не существует. Понятие длительности процессов, начинающихся в одной точке, а заканчивающихся в другой, теряет смысл, поскольку скорость хода часов в различных точках различна. Также трудно определить понятие длинны движущегося тела, если не ясно, что такое одновременность в различных точках. Эти трудности можно частично обойти, если принять во внимание, что интервал собственного времени не зависит от ускорения. Поэтому анализа пространственно-временных соотношений в некоторой бесконечно малой области НИСО можно воспользоваться пространственно-временными соотношениями ИСО, которая движется с той же скоростью, но без ускорения, как и соответствующая бесконечно малая область НИСО. Такая ИСО наз. сопровождающей. Рассмотрим движения с малыми скоростями, когда все эти трудности не возникают и можно использовать преобразования Галилея, считая, что пространственно-временные соотношения с НИСО таковы же, как если бы она была ИСО.

Силы инерции: переносная и кориолисова. В НИСО $ ускорения, которые не связаны с силами такого же характера, какие известны в ИСО. В НИСО, так же как и в инерциальных, ускорения вызываются силами, но наряду с «обычными» силами взаимодействия $ ещё и силы особой природы, называемые силами инерции. 2-ой з-н Ньютона формулируется без изменения, но наряду с силами взаимодействия необходимо учесть силы инерции. Силы инерции берутся такими, чтобы обеспечить в НИСО те условия, которые фактически имеются. 2-ой з-н Ньютона в НИСО: ma’=F+F_ин., где a’ – ускорение в НИСО, F – «обычные силы», F_ин – силы инерции. Переносная сила инерции направлена противоположно переносному ускорению НИСО и равна F_ин= – ma₀. Рассмотрим силы инерции во вращающейся СК:

F_ин=m(a’–a)=m(–a₀–a_K)=mw²R–2m[w v’]=F_цб+F_К. F_цб= mw²R – центробежная сила инерции. F_К=–2m[w v’] – сила инерции связанная с кориолисовым ускорением называется силой Кориолиса. Она перпендикулярна плоскости, в которой лежат векторы угловой и относительной скоростей. Если эти векторы колинеарны, то Кориолисово ускорение равно 0.