Центробежная и кориолисова силы инерции. Примеры проявления их действия.

Аабс=Аотн+2[w*Vотн]+dv0/dt+[w[wr]]+[dw/dt*r],2[w*Vотн]=Акор, [dw/dt*r]=Ацб, Fкор=-mАкор=2m[Vотн*w], Fцб=-[dw/dt*r]. Центробежные силы инерции существуют лишь в ускоренно движущихся (вращающихся) системах отсчета и исчезают при переходе к инерциальным системам. (Рассуждения на тему см. в Сивухине стр.374). бь

Примеры: пассажир в движ. транспорте на поворотах и т.п.

Кориолисова сила инерции возникает, когда матер. точка движется относительно вращающейся системы отсчета. От других сил инерции кориол. сила отличается тем, что она зависит от относительной скорости Vотн.

Пример: маятник Фуко, пассажир на повороте идет по автобусу и т.п.

Кориол. сила всегда перпендикулярна к относительной скорости, поэтому при относительном движении она не совершает работы. Следов., она является гироскопической силой (см. Сивухин, стр.145).

Пункт 2.

Сложение гармонических колебаний одинаковой частоты.x₁=A₁cos(wt+j₁), x₂=A₂cos(wt+j₂). Представим в комплексной форме: x=x₁+x₂=A₁e^i(wt+j1)+A₂e^i(wt+j2)=e^iwt(A₁e^ij1+A₂e^ij2), A₁e^ij1+A₂e^ij2=Ae^ij, A²=A₁²+A₂²+2A₁A₂cos(j₁–j₂,), tg j=(A₁sinj₁+A₂sinj₂)/(A₁cosj₁+A₂cosj₂) Þ x=x₁+x₂=Ae^i(wt+j) Þ x=Acos(w t–j).

Сложения гармонических колебаний с близкими частотами.x₁=A₁cos(w₁t+j₁), x₂=A₂cos(w₂t+j₂). Каждое из колебаний представим в комплексной форме, а сложение будем производить векторно. Пусть A₁>A₂. Cуммой двух колебаний с близкими частотами является колебание с изменяющейся амплитудой (от А₁–А₂ до А₁+А₂) и с частотой |w₁–w₂|. Колебания амплитуды с частотой W=|w₁–w₂| называются с биениями, а частота W – частотой биения.

Билет № 15.

Пункт 1. см. билет № 14. пункт 1.+ Опыт Гука. Закон Бэра. В северном полушарии правый берег выше левого(в общем). Износ рельсов.

Пункт 2.Затухающие колебания.Воспользуемся наиболее простым случаем «жидкого» или «вязкого» трения, когда сила трения направлениа противоположно скорости и пропорциональна скорости. Колебания при наличии трения становятся затухающими: . - коэффициент трения,

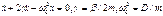
Решение этого уравнения удобно искать в виде

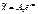. Учитывая, что ,

, находим

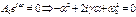
Решение этого уравнения: , где

,(*)

При не очень больших - вещественная величина и - гармоническая функция. Вещественная часть колебания, описываемого равенством (*), представляется формулой:

Отсюда видно, что амплитуда колебаний уменьшается в е=2,7 раза в течение времени -время затухания, а - показатель (коэффициент, декремент) затухания. Всё выше написанное относится к случаю не очень больших коэффициентов трения и когда W – действительное число.