Логарифмический декремент

, ,

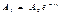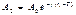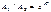
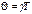- логарифмический декремент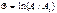

Другая интерпретация: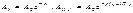

При 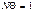амплитуда уменьшается в е раз, поэтому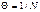

Добротность.Q=A_рез/А_ст=w₀/2d=2p/2dT=p/q, т. к. w_рез²=w₀²+2d².

Время релаксации: t=1/b. Время релаксации – характерное время установления равновесия в системе. Время релаксации – время за которое амплитуда убывает в e раз.

Билет № 16.

Пункт 2. Вынужденные колебания под действием гармонической внешней силы.Если на систему постоянно действует постоянно меняющаяся внешняя, зависящая от времени сила, то такие колебания наз. вынужденными.mx``=-Dx-bx`+F<sub>0</sub>coswt x``+2gx`+w₀²x=(F₀/m)coswt

Решение уравнения: x=A₀cos(wt+j) (в комплексной форме 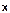(t)=A .) w - частота внешней силы, tg j = (2gw)/(w₀²-w²)

Процесс установления колебаний.Каковы бы ни были условия в момент начала действия внешней силы, осциллятор будет совершать одни и те же установившиеся гармонические колебания. Процесс установления колебаний называется переходным режимом. Он происходит потому, что с течением времени затухнут собственные колебания. Время установления колебаний определяется временем затухания колебаний, которые имелись в момент начала действия силы - t = 1/g. Даже если начальных колебаний не было, то все равно время установления будет тем же.

a) малые частоты: w<<w₀, w₀А=(F₀/m)sinwt, A(t)=( F₀/m w₀²)sinwt =( F₀/k) sinwt

б) большие частоты: w>>w₀, Ä@(F₀/m)sinwt, А=(F₀/mw²)sin(wt-p)

в) резонанс: w»w₀: Рассмотрим подробнее именно этот режим. С этой целью пе­репишем уравнение в комплексном виде:

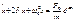(12.29) а его частное решение будем искать в виде 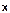(t)=A . (12.30) Реальная часть этого решения будет решением уравнения (12.27)(вместо в 12.29. cos wt) Подставляя (12.30) в (12.29), получаем 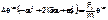Из условия стационарности решения (независимости его от вре­мени) следует, что a=w, откуда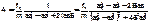

A есть комплексное число, которое удобно представить в экспоненциальном виде A=x+iY=Ao 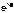. Тогда модуль А будет Aо= 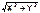, а его фаза tgj=Y/X. . Получаем, tg j = (2gw)/(w₀²-w²). Работа за период: A_пер.=(F₀²bw²T)/((w²₀-w²)+4w²b²)

Билет № 17.

Пункт 1.

Точкой приложения равнодействующей сил назовем геом. Точку относительно которой сумма моментов всех этих сил равна 0.

Массовыми назовем силы пропорциональные массам. Силы тяготения вообще говоря не являются массовыми. Их можно считать массовыми, если размеры рассматриваемой области, шде материальные точки подвержены действию гравитационных сил, достаточно малы.

Центром масс системы мат. Точек является точка приложения всех массовых сил.

Центр тяжести – точка приложения равнодействующей всех сил тяжести.

Центр инерции – точка приложения равнодействующей всех сил инерции.

Центр масс, Центр тяжести и центр инерции совпадают если силы тяжести и силы инерции являются массовыми

Принцип эквивалентности Эйнштейна. Силы инерции и силы тяготения эквивалентны друг другу (и локально не различимы).

Пункт 2. АЧХ и ФЧХ. Резонанс.

АЧХ-кривая,описывающая зависимость амплитуды вынужденных установившихся колебаний от частоты внешней силы.

ФЧХ-то же для разности фаз вынужденных колебаний и внешней силы. резонанс: w»w₀ А=А₀sin(w₀t+j) Ä+w₀²A=0 2gÁ=(F₀/m)sinw₀t

A=(F₀/2mgw₀)sin(wt-p/2) A₀=F₀/2mgw₀=( F₀/mw₀²)*(w₀/2p)=(F₀/k)*Q

tg j = (2gw)/(w₀²-w²)

½(w₀-w)/w½ << 1

(w₀²-w²)² = (w₀-w)²*(w₀₊w)²; w₀₊w ≈ 2ω; 4γ²ω² ≈ 4γ²ω₀²

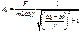– Формула Лоренца

∆ω = 2δ=ω₀/Q - ширина резонансной кривой.g=d — дектремент затухания.

W=(ω₀²-g²)^1/2.

Билет № 18.

1. Постулат относительности. Все законы механики и электромагнетизма имеют один и тот же вид во всех инерциальных системах отсчета.

2. Постулат постоянства скорости света. Свет распространяется во всех инерциальных системах отсчета в вакууме с одинаковой универсальной скоростью, равной C.

Пункт 2. Не сделано.

Билет № 19.

Преобразования Лоренцаобоснованы на принципе относительности (Утверждение, впервые высказанное Г. Галилеем, о том, что во всех инерциальных системах координат механические явления протекают одинаково, называется принципом относительности Галилея. В дальнейшем в результате изучений других явлений, в частности электромагнитных, справедливость этих положений была признана для любых явлений. В таком общем виде оно называется принципом относительности СТО или просто принципом относительности) и принципа постоянства скорости света (независимость скорости света от скорости источника и скорости наблюдателя. Это постулат).

Однородность пространства:начало системы координат может быть помещено в любой точке и все геометрические соотношения между любыми геометрическими объектами при этом совершенно одинаковы с теми, которые получаются при помещении начала координат в любую другую точку.

Изотропность пространства:в каждой точке пространства можно ориентировать оси СК произвольным образом. При этом соотношения между геометрическими обьектами не имменются.

Однородность и изотропность времени является его главными свойствами в ИСО.

Однородность времени:это одинаковость развития и изменения данной физической ситуации независимо от того, в какой момент эта ситуация сложилась.

Из однородности пространства и времени следует, что преобразования должны быть линейными. x’=Ф1(x,y,z,t),

y’=Ф(x,y,z,t),

z’=Ф3(x,y,z,t),

t’=Ф4(x,y,z,t).

Исходя из изотропности и однородности пространтва, мы можем как угодно поворачивать и смещать оси СК. ориентируем оси так:

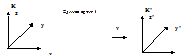
Начало координат: Пусть в t=0 x=y=z=0 совпадает с x’=y’=z’=0 , тогда А5=0

y’ = a1x + a2y + a3z + a4t;

z’ = b1x + b2y + b3z + b4t;

Т.к. оси Y,Y’ и Z,Z’ параллельны след: y=0 y’=0, z=0 z’=0

0 = a1x + a3z + A4t;

0 = b1x + b2y + b4t; что возможно лиш при а1=а3=а4=0 0=в1=в3=в4 След. y’=ay и z’=az y=y’/a z=z’/a так как масштаб в С.К. изменятся одинаково, значит а=1/а , значит а=1. Следовательно y’=y; z=z’.

Преобразования для x и t:Вследствие линейности преобразований: x’=a(x–vt) Þ x=a’(x’+vt)

Докажем, что a’=a. Пусть некоторый стержей покоится в системе К’: x₂’–x₁’=l. В системе К он движется Þ x₁’=a(x₁–vt₀), x₂’=a(x₂–vt₀) Þ x₂ –x₁=(x₁’–x₂’)/a=l/a..

Пусть теперь тот же стержень в системе К и имеет в ней длину l. Þ x₂–x₁=l. В системе К’, принятой за неподвижную, этот стержень двигается с v. Þ x₁=a’(x₁’+v₀ t’), x₂=a’(x₂’+v₀ t’) Þ x₂’–x₁’=(x₂–x₁)/a’. Согласно принципу относительности обе системы равноправны и длинна одного и того же стержня, движущегося в этих системах с одинаковой скоротью, должна быть обнакова Þ a’=a. Воспользуемся постулатом скорости света: x’=ct’, x=ct. Þ

ct’=a t(c–v), ct=a t’(c+v) Þ a= Þ vt’=(x/a)–x’=(x/a)–a(x–vt)=avt+x((1/a)–a)Þt’= , x’= 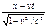, y=y’, z=z’. Обратные преобразования получаются заменой штрухованных элементов на нештрихованные и измененим знака скорости.

Инвариантом преобразований Лоренца явл. пространтвенно-временной интревал или просто интервал. Интервалом между точками (x₁, y₁, z₁, t₁) и (x₂, y₂, z₂, t₂) наз. величина s=(x₁–x₂)²+(y₁–y₂)²+(z₁–z₂)²–c²(t₁–t₂)²– эта величина имеет во всех СК одно и то же значения, т. е. явл. инвариантом преобразований Лоренца.

s²>0 Þ интервал пространственноподобный.

s²<0 Þ интервал времениподобный.

s²=0 Þ интервал нулевой (такой интервал $ существуе между событиями, которые могут быть связаны сигналом, распространяющимся со скоростью света).

Время, которое измеряется по часам, связанным с движущейся точкой, наз. собственным временем этой точки.

Длина, которая измеряется прибором, связанным с движущимся стержнем, наз. абсолютной длинной.

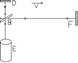Опыт Майкельсона.Идея опыта состоит в сравнении прохождения светом двух путей, из которых один совпадает с направлением движения тела в эфире, а другой ему перпендикулярен (свет рассматривался как волновой процесс в среде, эту среду назвали “мировым эфиром”.)

Луч монохромного света (света определенной частоты) из источника A падает на полупрозрачную пластину B, расположную под углом 45 градусов. Здесь луч разделяется на два когерентных луча: один отражается от пластинки и направляется к зеркалу D, а другой проходит через пластинку и направляется к зеркалу F. От зеркал D и F лучи света отражаются и возвращаются к пластинке B. Луч, частично отразившись от D и пройдя сквозь полупрозрачную пластинку B, встречается в интерферометре E, с лучом, отразившимся от зеркал F и пластинки B. Таким образом, в интерферометре встречаются два когерентных луча, прошедших от места разделения два различные пути. Ясно, что если эти пути пройдены ими за одинаковое время, то в точке встречи между их колебаниями имеется та же самая разность фаз j, как и в точке разделения. Изменение освещенности в зависимости от разности фаз слагаемых световых колебаний называется интерференцией. Наблюдая интерференцию, можно сделать заключение о разности фаз пришедших в интерферометр когерентных волн, а отсюда вычислить время запаздывания одной волны относительно другой.

Расчет разности хода лучей. BF||V: t_bf =l1/(c-v), t_fb =l1/(c+v), t_|| =(2L1/c)*(1/(1-V^2/c^2)). t_bd = t_db =L2/c_перп.=(L2/c)*(1/)( Ö1-v^2/c^2), t_перп.=(2*L2/c)*(1/( Ö1-v^2/c^2)). Величина (V^2/c^2) имеет порядок 10^-8, поэтому можно разложить t_перп и t_|| в ряд относительно этой величины и ограничится первым членом. t_|| =(2L1/c)*(1+V^2/c^2), t_перп.=(2*L2/c)*( 1+1/2*v^2/c^2). Следовательно, разность времени хода лучей равна: dt(1)=(2/c)*(v^2/c^2)(L1-L2/2)+(2/c)(L1-L2). Теперь повернем прибор на 90 градусов. BD||V разность хода вычисляется аналогично но следует заменить l1 на l2. Учитывая, что l1 перпендикулярно скорости, а l2 паралельно, получаем: dt(2)= -(2/c)*(v^2/c^2)(L2-L1/2)-(2/c)(L2-L1). Таким образом полное изменение разности хода лучей по времени при попороте прибора на 90 градусов равно: dt=-((l1+l2)/c)* (v^2/c^2).

Результаты опыта: скорость света во всех направлениях одинакова.