КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематика поступательного и вращательного движения
Краткая теория
· Радиус-вектор материальной точки задаёт положение её в пространстве (рис.1.1):
,
где x, y и z – координаты точки; 
– единичные векторы (орты), направленные вдоль осей OX, OY и OZ соответственно. Модуль вектора 
:
.
· Кинематическое уравнение движения:
;
или в координатной форме:
где t – время.
· Средняя скорость:
,
где 
– перемещение материальной точки за интервал времени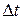 
, 
и 
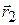– радиус-векторы начального и конечного положения точки соответственно.
· Средняя путевая скорость (средняя скорость вдоль траектории):
где 
– путь (длина траектории), пройденный точкой за интервал времени .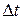
· Мгновенная скорость:
; 
,
где 
, 
, 
– проекции скорости 
на оси координат.
· Модуль скорости:
.
· Закон сложения скоростей:
,
где – абсолютная, 
– переносная, 
– относительная скорости.
· Ускорение:
; 
,
где 
, 
, 
– проекции ускорения 
на оси координат.
· Модуль ускорения: 
.
· При равномерном движении 
и 
.
· Кинематическое уравнение равномерного движения материальной точки:
,
или вдоль оси х:
,
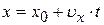где 
и 
– радиус-вектор и координата начального положения точки; 
и 
– начальная скорость и её проекция на ось OX; t – время.
· При равнопеременном движении 
.
· Скорость точки при равнопеременном движении:
,
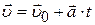или в проекции на ось OX:
.
где и 
– ускорение и его проекция на ось OX.
· Кинематическое уравнение равнопеременного движения:
или вдоль оси x:
.
Криволинейное движение
· Ускорение при криволинейном движенииможно представить как сумму нормальной 
и тангенциальной 
составляющих (рис.1.2):
;
.
· Нормальное ускорение равно
и направлено к центру кривизны траектории перпендикулярно ей. Здесь R – радиус кривизны траектории в данной точке.
· Тангенциальное (касательное) ускорение равно
и направлено по касательной к траектории.
· Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) φ.
· Кинематическое уравнение вращательного движения:
.
· Средняя угловая скорость:
,
где 
–угол поворота за интервал времени .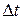
· Мгновенная угловая скорость:
.
· Угловое ускорение:
.
Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения (рис.1.3).
· Связь между угловыми величинами и линейными:
;
;
,
,
где – путь, пройденный точкой по дуге окружности радиусом R, – соответствующий угол поворота,
· При равномерном вращении 
, 
.
· Кинематическое уравнение равномерного вращения:
,
где 
– начальная угловая координата; t – время.
· Частота вращения:
,
где N – число оборотов, совершаемых телом за время t; Т – период вращения (время одного полного оборота).
· Связь угловой скорости с периодом и частотой:
.
· При равнопеременном вращательном движении 
.
· Угловая скорость при равнопеременном вращении:
,
где – начальная угловая координата; 
– начальная угловая скорость, t – время, ε – угловое ускорение.
· Кинематическое уравнение равнопеременного вращения ( .)
.
Дата добавления: 2014-10-31; просмотров: 153; Мы поможем в написании вашей работы!; Нарушение авторских прав |