КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Молекулярно-кинетическая теория
Краткая теория
Относительная молекулярная (атомная) масса – отношение массы молекулы (атома) 
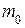данного вещества к 
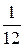массы атома углерода 
(изотопа 12С):
.
Моль – количество вещества, в котором содержится столько же молекул или атомов, сколько атомов содержится в 0.012 кг углерода 12С.
В одном моле любого вещества содержится одно и то же число молекул или атомов,которое называется числом (постоянной) Авогадро. Число Авогадро равно
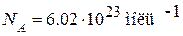
Количество вещества ν – число молей, равное отношению числа молекул N к числу Авогадро:
.
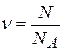Молярная массаµ – масса одного моля вещества:
,
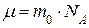где 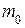– масса одной молекулы; 
– число Авогадро. Поскольку масса вещества – это произведение массы одной молекулы на их количество: 
, то количество вещества равно:
.
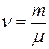Относительная молекулярная масса вещества:
,
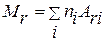где ni – число атомов i-го химического элемента, входящего в состав молекулы данного вещества; 
– относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева.
Связь молярной массы с относительной молекулярной массой:
.
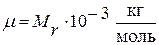Давление, производимое газом на стенки сосуда:
,
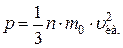где n – концентрация молекул; 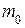– масса одной молекулы; 
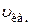– средняя квадратичная скорость молекул.
Концентрация молекул – число молекул в единице объёма:
.
Средняя квадратичная скорость (по определению):
,
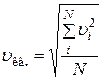где N – число молекул; суммирование происходит по всем молекулам. Или:
,
где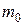 
– масса молекулы; 
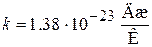– постоянная Больцмана; Т – термодинамическая температура µ – молярная масса газа; 
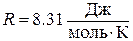– универсальная газовая постоянная.
Универсальная газовая постоянная равна
,
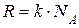где k – постоянная Больцмана; – число Авогадро.
Уравнение состояния идеального газа (уравнениеМенделеева-Клапейрона:
, или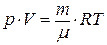 
,
где m – масса газа; µ – его молярная масса; Т – термодинамическая температура;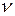 
– количество вещества; R – универсальная газовая постоянная.
Термодинамическая температура (температура по шкале Кельвина):
,
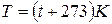где t – температура в градусах Цельсия.
Давление газа равно:
,
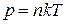где k – постоянная Больцмана; n – концентрация молекул, Т термодинамическая температура.
Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений входящих в смесь газов:
,
где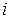 
– номер компоненты смеси; 
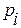– её парциальное давление, то есть то давление, которое производил бы данный сорт газа, если бы только один занимал весь объём, равный полному объёму смеси; K – число компонентов смеси.
Массовая доля i-го компонента смеси газов
,
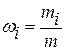где mi – масса i-го компонента смеси; m – масса смеси.
Основное уравнение молекулярно-кинетической теории
– для давления:
;
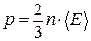– для температуры:
,
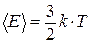где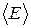 
– средняя кинетическая энергия поступательного движения молекул газа.
Теорема о равнораспределении энергии по степеням свободы. На любую степень свободы приходится в среднем одинаковая энергия, равная
.
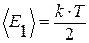Число степеней свободы 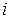равно числу независимых координат, однозначно определяющих положение тела (или молекулы) в пространстве. Для одноатомных молекул 
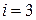, для двухатомных 
, для произвольных жёстких многоатомных – 
.
Средняя энергия одной молекулы, у которой 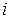степеней свободы, равна
.
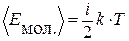Внутренняя энергия U идеального газа:
,
где i – число степеней свободы молекул газа.
Дата добавления: 2014-10-31; просмотров: 160; Мы поможем в написании вашей работы!; Нарушение авторских прав |