КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Динамика материальной точки
Краткая теория
· Второй закон Ньютона (уравнение движения материальной точки):
, или 
,
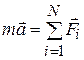где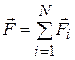 
– векторная сумма сил, действующих на материальную точку (равнодействующая всех сил); т – масса; 
– ускорение; N – число сил, действующих на точку.
В проекциях на координатные оси:
; 
, 
,
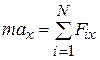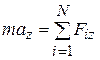или
; 
, 
,
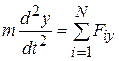где под знаком суммы стоят проекции сил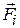 
, на соответствующие оси.
· Импульс тела массой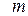 
, движущегося со скоростью 
:
.
При скоростях 
, сравнимых со скоростью света в вакууме (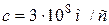 
), необходимо использовать формулы для релятивистского импульса:
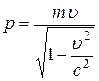или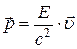 
,
где Е – полная энергия частицы, равная сумме энергии покоя 
и кинетической энергии: 
. Полная энергия частицы и её импульс связаны следующей релятивистской формулой:
.
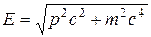· Импульс силы:
,
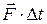где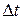 
– промежуток времени, в течение которого действовала сила 
.
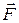· Второй закон Ньютона в импульсной форме:
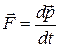, или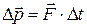 
где 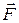– равнодействующая, 
– импульс тела, 
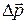– изменение импульса за промежуток времени 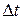действия силы.
· Третий закон Ньютона. Тела действуют друг на друга с силами, равными по величине и направленными противоположно вдоль одной прямой:
,
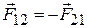где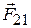 
– сила, с которой первое тело действует на второе, а 
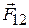– второе на первое.
· Центр масс. Радиус-вектор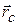 
центра масс равен
,
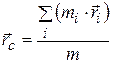где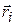 
– радиус-вектор точечной массы 
, 
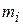– масса всей системы (тела).
Координаты центра масс системы материальных точек:
, 
, 
,
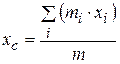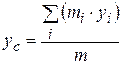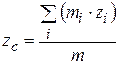где xi, yi;, zi – координаты i-й материальной точки.
Закон всемирного тяготения
,
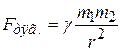где γ – гравитационная постоянная; m1 и m2 – массы взаимодействующих тел, рассматриваемые как материальные точки; r – расстояние между ними.
Сила притяжения тела массой m к Земле (или другому небесному телу) массой M радиусом R на высоте h над поверхностью (сила тяжести):
.
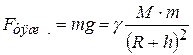Здесь γ – гравитационная постоянная, g – ускорение свободного падения на высоте h: 
.
Сила тяжести на поверхности Земли:
,
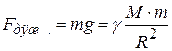где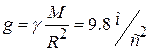 
– ускорение свободного падения
Вес тела, движущегося с ускорением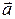 
:
,
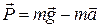где m – масса тела. Если ускорение тела направлено вертикально вверх, то вес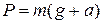 
; а если вертикально вниз, то 
.
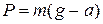Сила трения скольжения:
,
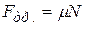где 
– коэффициент трения скольжения; N – сила нормального давления.
Сила упругости (закон Гука):
,
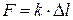где k – коэффициент упругости (коэффициент жесткости); 
– абсолютная деформация.
Относительная продольная деформация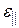 
(или просто 
) – это изменение длины тела по отношению к первоначальной длине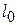 
(рис.2.1):
.
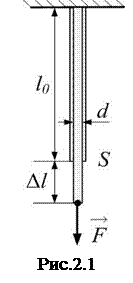
Механическое напряжение (нормальное механическое напряжение) σ – это сила, приходящаяся на единицу площади сечения тела (сила приложена перпендикулярно сечению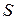 
):
.
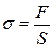Закон Гука в локальной (дифференциальной) форме:
,
где 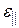– относительная деформация; σ – механическое напряжение; 
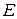– модуль Юнга материала.
Давление – это сила F, приходящаяся на единицу площади S:
.
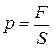Плотность тела
,
где m – масса тела; V – его объём.
Гидростатическое давление:
,
где ρ – плотность; g – ускорение свободного падения; h – глубина под свободной поверхностью жидкости.
Выталкивающая (Архимедова) сила:
,
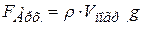где ρ – плотность жидкости (газа); Vпогр. – объём погружённой части тела.
Момент силы:
,
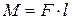где l – плечо силы (кратчайшее расстояние от линии силы до оси вращения).
Условие равновесия твёрдого тела
равнодействующая всех сил равна нулю:
;
сумма моментов всех сил относительно любой оси тоже равна нулю:
.
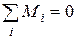Дата добавления: 2014-10-31; просмотров: 197; Мы поможем в написании вашей работы!; Нарушение авторских прав |