
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Законы сохранения. Закон сохранения импульса: в замкнутой системе полный импульс сохраняется.
Краткая теория
 Закон сохранения импульса: в замкнутой системе полный импульс сохраняется.
Закон сохранения импульса: в замкнутой системе полный импульс сохраняется.
Закон сохранения импульса справедлив и в случае, если внешние силы действуют на систему, но компенсируют друг друга:
если  , то
, то  (или
(или 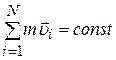 ).
).
где N — число материальных точек (или тел), входящих в систему.
Даже если равнодействующая внешних сил не равна нулю, но равна нулю её проекция на какую-либо ось, то проекция полного импульса системы на ту же ось сохраняется:
если  , то
, то 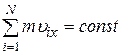 .
.
 Работа, совершаемая постоянной силой:
Работа, совершаемая постоянной силой:
 ,
,
где  – угол между направлениями векторов силы
– угол между направлениями векторов силы 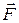 и перемещения
и перемещения 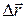 .
.
 Работа, совершаемая переменной силой:
Работа, совершаемая переменной силой:
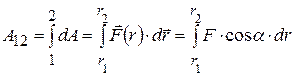 ,
,
где интегрирование ведется вдоль траектории от точки 1 с радиус-вектором  до точки 2 с радиус-вектором
до точки 2 с радиус-вектором 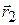 .
.
 Средняя мощность – работа за единицу времени:
Средняя мощность – работа за единицу времени:
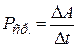 ,
,
где ΔА – работа, совершённая за время Δt.
 Мгновенная мощность – быстрота совершения работы:
Мгновенная мощность – быстрота совершения работы:
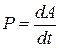 , или
, или  .
.
 Коэффициент полезного действия (КПД):
Коэффициент полезного действия (КПД):
 .
.
 Кинетическая энергия материальной точки (или тела), движущейся поступательно:
Кинетическая энергия материальной точки (или тела), движущейся поступательно:
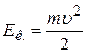 , или
, или 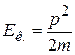 .
.
 Потенциальная энергия тела в однородном поле силы тяжести:
Потенциальная энергия тела в однородном поле силы тяжести:
 ,
,
где h – высота тела над уровнем, принятым за начало отсчета. Эта формула справедлива при условии 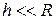 , где R – радиус Земли. Если это условие не соблюдается, то
, где R – радиус Земли. Если это условие не соблюдается, то
 .
.
Здесь 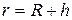 – расстояние до центра планеты.
– расстояние до центра планеты.
 Потенциальная энергия упруго деформированного тела:
Потенциальная энергия упруго деформированного тела:
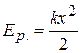 ,
,
где k – жёсткость (коэффициент упругости), x=Δl – абсолютная деформация (удлинение) тела.
 Закон сохранения энергии. Полная энергия замкнутой системы сохраняется:
Закон сохранения энергии. Полная энергия замкнутой системы сохраняется:
если 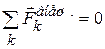 , то
, то 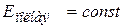 , или
, или  ,
,
где Е1 – начальная полная энергия системы (сумма всех видов энергии: механической, внутренней, электромагнитной и т.д.); Е2 – конечная полная энергия системы.
 Закон сохранения механической энергии. Полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, остаётся постоянной:
Закон сохранения механической энергии. Полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, остаётся постоянной:
если 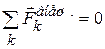 , то
, то 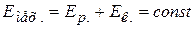 , или
, или  .
.
При наличии диссипативных сил (силы трения, вязкости, силы неупругой деформации) закон сохранения (изменения) механической энергии при переходе системы из состояния 1 в состояние 2:
 ,
,
Если есть любые внешние силы:
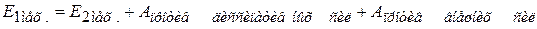 .
.
Дата добавления: 2014-10-31; просмотров: 394; Мы поможем в написании вашей работы!; Нарушение авторских прав |