Момент импульса материальной точки. Момент силы. Уравнение моментов. Закон сохранения момента импульса.

Момент импульса материальной точки относительно точки представляет собой векторное произведение радиус-вектора материальной точки, проведенного из точки 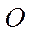, и ее импульса :

, модуль момента импульса рассчитывается по формуле: , где − угол между векторами и ; − плечо импульса. Направление вектора момента импульса определяется по векторному произведению.

Моментом импульса относительно закрепленной оси называется проекция 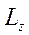на эту ось момента импульса . Момент импульса относительно оси определяется проекцией импульса точки на плоскость, перпендикулярную к оси , где − момент инерции материальной точки (тела) относительно оси , − угловая скорость вращения материальной точки (тела) относительно этой оси.

Момент силы относительно точки представляет собой векторное произведение радиус-вектора материальной точки и силы , действующей на эту материальную точку: ,

модуль момента силы рассчитывается по формуле: , где − угол между векторами и ; − расстояние между точкой 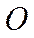и линией действия силы − плечо силы. Направление вектора момента силы определяется по векторному произведению.

Моментом силы относительно закрепленной оси вращения , проходящей через точку , называют проекцию вектора 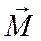на ось 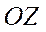. Если разложить радиус вектор материальной точки и силу на составляющие параллельную и перпендикулярную к оси : , то составляющие, параллельные оси не дадут вклад в проекцию момента на ось. Следовательно,

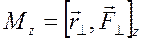
Закон сохранения момента импульса −суммарный момент импульса замкнутой системы материальных точек не изменяется с течением времени: .