Колебания. Гармонические колебания и их основная характеристика. Графическое представление гармонических колебаний и представление в комплексной форме.

Колебания – периодически повторяющиеся с течением времени изменения физической велечины.

Гармонические колебания − колебания физической величины, происходящие по гармоническому закону − по закону или .

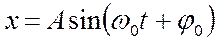Уравнение гармонических колебаний: или , где 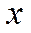− смещение тела из положения равновесия; − амплитуда гармонических колебаний − максимальное смещение тела из положения равновесия; − фаза гармонических колебаний; − фаза колебаний в начальный момент времени; − циклическая частота или собственная частота гармонических колебаний; 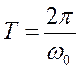− период гармонических колебаний − время, за которое совершается одно полное колебание; 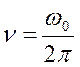− частота гармонических колебаний − количество колебаний, совершаемых за единицу времени.

Рассмотрим графический способ представления гармонического колебания

.

Выберем координатную ось . Из начала координат (точки ) проведем вектор , длина которого равна амплитуде рассматриваемого гармонического колебания , а направление вектора образует с осью угол 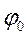, равный начальной фазе колебаний. Тогда проекция вектора на координатную ось в начальный момент времени будет равна , т.е. представляет собой смещение системы из положения равновесия в начальный момент времени. Если заставить вектор вращаться с постоянной угловой скоростью (равной собственной частоте гармонических колебаний) вокруг начала координат 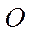, то угол между направлениями вектора и оси будет изменяться с течением времени по закону 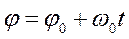. В это случае проекция вектора на координатную ось в любой произвольный момент времени будет равна 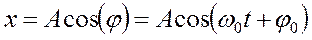, т.е. представляет собой смещение системы из положения равновесия в момент времени .

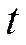Скорость, ускорение и энергия (потенциальная, кинетическая, полная) гармонических колебаний.

Скорость материальной точки, совершающей гармонические колебания:

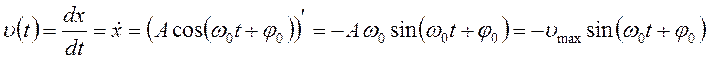, где − максимальная скорость материальной точки.

Ускорение материальной точки, совершающей гармонические колебания:

, где − максимальное ускорение материальной точки.

Энергия материальной точки, совершающей гармонические колебания:

кинетическая энергия ,

потенциальная энергия ,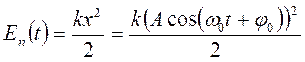

полная энергия гармонических колебаний .