Модель гармонического осциллятора. Пружинный маятник. Математический и физический маятник.

Математический маятник −материальная точка, подвешенная на невесомой нерастяжимой нити.

Период и собственная циклическая частота колебаний математического маятника: , , где − длина нити маятника; − ускорение свободного падения.

Физический маятник − тело, способное совершать свободные колебания относительно оси, проходящей выше центра масс.

Период и собственная циклическая частота колебаний физического маятника: , , где − момент инерции маятника относительно оси, проходящей через точку подвеса; − масса маятника; − расстояние между точкой подвеса и центром масс маятника; − ускорение свободного падения.

Пружинный маятник − тело, подвешенное на невесомой пружине.

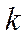Период и собственная циклическая частота колебаний математического маятника: , , где − масса маятника; −коэффициент жесткости пружины.

Гармонический осциллятор – материальная точка, совершающая малые колебания около положения равновесия под действием квазиупругой силы.
Законы Кеплера. Космические скорости.

I Закон: Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.

II Закон: Радиус-вектор планеты за равные интервалы времени описывает одинаковые площади.

III Закон: Квадраты периодов обращения любых двух планет относятся как кубы больших полуосей их орбит: .

Законы Кеплера справедливы также для движения спутников вокруг планеты.

Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:

v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг НТ и не падать на поверхность НТ).

v2 — преодолеть гравитационное притяжение небесного тела.

v3 — покинуть звёздную систему, преодолев притяжение звезды.

v4 — покинуть галактику, преодолев притяжение сверхмассивной черной дыры.
Вынужденные колебания. Дифференциальное уравнение для вынужденных колебаний и его решение.

Вынужденные колебания − колебания, которые совершаются при наличии внешнего периодически изменяющегося воздействия.

Дифференциальное уравнение вынужденных колебаний при наличии силы сопротивления 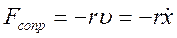и изменяющейся по гармоническому закону вынуждающей силы :

, где − смещение тела из положения равновесия; − масса материальной точки (тела), − скорость материальной точки; − коэффициент сопротивления; − ускорение материальной точки; −коэффициент затухания; − циклическая частота собственных незатухающихколебаний.

Уравнение установившихся вынужденных колебаний:

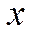, где − смещение тела из положения равновесия; − циклическая частота вынужденных колебаний;

− амплитуда вынужденных колебаний;

− разность фаз между колебаниями вынуждающей силы и тела.

Амплитуда вынужденных колебаний зависит от соотношения между циклическими частотами вынуждающего воздействия 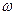и собственных колебаний . Резонансная частота и резонансная амплитуда , .