Движение точки по окружности. Угол поворота, угловая скорость, частота и период обращения. Связь между линейной и угловой скоростью.

При вращении материальной точки вокруг неподвижной оси вводится вектор углового перемещения , модуль которого равен углу поворота , а направление вектора связано с направлением вращения правилом правого винта (т.о. вектор углового перемещения является аксиальным вектором).

Угловая скорость (мгновенная) − векторная величина, равная первой производной угла поворота материальной точки по времени: 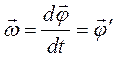, где − угол поворота материальной точки при движении по окружности.

Модуль угловой скорости: ;

Направление вектора определяется по правилу правого винта: если рукоятку правого винта вращать в направлении движения материальной точки по окружности, то направление движения острия винта совпадает с направлением вектора угловой скорости .

При равномерном движении по окружности — движении с постоянной угловой скоростью используются следующие характеристики:

Период обращения по окружности − время, за которое материальная точка (тело) совершает один полный оборот при движении по окружности: ;

Частота 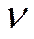обращения по окружности − количество оборотов, совершаемых материальной точкой (телом) за единицу времени при движении по окружности: .

Связь между линейной и угловой скоростью

, где − вектор скорости материальной точки; − вектор угловой скорости материальной точки; − радиус-вектор материальной точки.

Для модулей векторов: 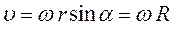, где − модуль скорости материальной точки; − модуль угловой скорости материальной точки; 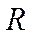− радиус окружности, по которой движется материальная точка; − угол между направлениями векторов и .