Изопроцессы

Изопроцессы - это процессы, протекающие при неизменном значении одного из макроскопических параметров (р, V, Т).

Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называют изотермическим.

Изотермический процесс описывает закон Бойля- Мариотта, открытый в 1861 г. английским ученым Р. Бой-лем (1627-1691) и в 1876 г. французским ученым Э. Мари-оттом (1620-1684). При постоянной массе газа pV = const.

Для газа данной массы произведение давления на его объем постоянно, если температура не меняется.

Графики изотермического процесса в координатах р-V; р-Т; V-Т имеют следующий вид (рис. 27):

Процесс изменения состояния термодинамической системы при постоянном давлении называется изобарным. Из уравнения Менделеева-Клапейрона следует, что при

постоянной массе газа

Для данной массы газа отношение объема к температуре постоянно, если давление газа не меняется.

Этот закон был установлен экспериментально в 1802 г. французским ученым Ж. Гей-Люссаком (1778-1850).

Графики изобарического процесса в координатах р-V; V-Т; р-Т имеют следующий вид (рис. 28):

Процесс изменения состояния термодинамической системы при постоянном объеме называется изохорным. Из уравнения Менделеева-Клапейрона можно записать:

Для данной массы газа отношение давления к температуре постоянно, если его объем не меняется. Графики изохорного процесса в координатах р-V; V-Т; р-Т имеют следующий вид (см. рис. 29). Этот закон был установлен экспериментально в 1787 г. Ж. Шарлем (1746-1823).

16!

Вну́тренняя эне́ргия — принятое в физике сплошных сред, термодинамике и статистической физике название для той части полнойэнергии термодинамической системы, которая не зависит от выбора системы отсчета^[1] и которая в рамках рассматриваемой проблемы может изменяться^[2]. То есть для равновесных процессов в системе отсчета, относительно которой центр масс рассматриваемого макроскопического объекта покоится, изменения полной и внутренней энергии всегда совпадают. Перечень составных частей полной энергии, входящих во внутреннюю энергию, непостоянен и зависит от решаемой задачи. Иначе говоря, внутренняя энергия — это не специфический вид энергии^[3], а совокупность тех изменяемых составных частей полной энергии системы, которые следует учитывать в конкретной ситуации.

Деление полной энергии системы на потенциальную, кинетическую, внутреннюю и т. д. зависит от формальных определений этих понятий и поэтому достаточно условно^[4]. Так, иногда во внутреннюю энергию не включают потенциальную энергию, связанную с полями внешних сил^[2][5][6]. Важно, что правильность получаемых при решении конкретной задачи результатов зависит от корректности составления уравнения энергетического баланса, а не от терминологических нюансов.

Воспринимаемые органами чувств человека нагрев или охлаждение макроскопического объекта есть проявления изменения внутренней энергии этого объекта. Обратное неверно: постоянство температуры объекта не означает неизменность его внутренней энергии. Первое начало (закон) термодинамики представляет собой конкретизацию закона сохранения энергии для термодинамических систем. В рамках традиционного подхода первое начало формулируют как соотношение, устанавливающее связь между внутренней энергией, работой и теплотой: одна из этих физических величин задаётся с помощью двух других, которые, будучи исходными объектами теории, в рамках самой этой теории определены быть не могут просто потому, что не существует понятий более общих, под которые можно было бы подвести подлежащие определению термины^[22]. В соответствии с интерпретацией Г. Гельмольца первое начало трактуют как определение внутренней энергии для закрытых систем^[23]:

(Первое начало в формулировке Гельмгольца)

где — изменение внутренней энергии системы в равновесном термодинамическом процессе, — количество теплоты, полученное системой в этом процессе, — работа, совершенная системой. В этом выражении использовано «теплотехническое правило знаков для теплоты и работы».

Термодинамика заимствует понятия энергии и работы из других разделов физики, тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. По этой причине логичнее сразу трактовать первое начало так, как это делали Клаузиус^[19] и его последователи, а именно, как определение теплоты через внутреннюю энергию и работу^[24]. С использованием «теплотехнического правила знаков» математическое выражение для первого начала в формулировке Клаузиуса имеет вид:

(Первое начало в формулировке Клаузиуса)

Первое начало в формулировке Гельмгольца вводит внутреннюю энергию как физическую характеристику системы, поведение которой определяется законом сохранения энергии, но не определяет её как математический объект, т. е. функцию конкретных параметров состояния^[25]. Альтернативное определение внутренней энергии предложено К. Каратеодори (1909), который сформулировал первое начало термодинамики в виде аксиомы о существовании внутренней энергии — составной части полной энергии системы — как функции состояния, зависящей для простых систем^[26] от объёма системы , давления и масс составляющих систему веществ , , …, , …^[27]:

(Первое начало в формулировке Каратеодори)

Важно, что данное определение внутренней энергии справедливо для открытых систем^[28]. В формулировке Каратеодори внутренняя энергия не представляет из себяхарактеристическую функцию своих независимых переменных.

Калорические уравнения состояния[править | править вики-текст]

Внутренняя энергия системы есть однозначная, непрерывная и ограниченная функция состояния системы^[29]. Для определённости полагают внутреннюю энергию ограниченной снизу. За начало отсчёта внутренней энергии принимают её значения при абсолютном нуле температуры^[30]. Уравнение, выражающее функциональную зависимость внутренней энергии от параметров состояния, носит название калорического уравнения состояния^[31][32]. Для простых однокомпонентных систем калорическое уравнение связывает внутреннюю энергию с любыми двумя из трёх параметров 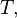т. е. имеется три калорических уравнения состояния:

(Калорическое уравнение состояния с независимыми переменнымиT и V)

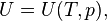
(Калорическое уравнение состояния с независимыми переменными Tи p)

(Калорическое уравнение состояния с независимыми переменными Vи p)

Выбор независимых переменных для калорического уравнения состояния, теоретически не имеющий принципиального значения, важен с практической точки зрения: удобнее иметь дело с непосредственно измеримыми величинами типа температуры и давления.

Применение термодинамики для решения практических задач часто требует знания параметров, конкретизирующих свойства изучаемого объекта, т. е. требуетсяматематическая модель системы, с необходимой точностью описывающая её свойства. К таким моделям, называемым в термодинамике уравнениями состояния, относятся термическое и калорическое уравнения состояния. Для каждой конкретной термодинамической системы её уравнения состояния устанавливают по экспериментальным данным или находят методами статистической физики, и в рамках термодинамики они считаются заданными при определении системы^[33]. Если для системы известны её термическое и калорическое уравнения состояния, то тем самым задано полное термодинамическое описание системы и можно вычислить все её термодинамические свойства^[32].

15! В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна

Так как в одном киломоле содержится молекул, то внутренняя энергия одного киломоля газа будет

Учитывая, что , получим

Для любой массы m газа, т.е. для любого числа киломолей внутренняя энергия

(10.12)

Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества

17! В изобарном процессе расширения газа P = const. Следовательно, при любом сколь угодно большом увеличении объема сила давления газа будет постоянной, и формула работы сохранит свой вид

A = P·(V2 - V1).

18! ервый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:
Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.
ΔU = Q – A.
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
Q = ΔU + A.
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.

Применим первый закон термодинамики к изопроцессам в газах.

В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно,
Q = ΔU = U (T2) – U (T1).
Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля) . При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением
A = p (V2 – V1) = p ΔV.
Первый закон термодинамики для изобарного процесса дает:
Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV.
При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.

В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.

Первый закон термодинамики для изотермического процесса выражается соотношением
Q = A.
Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.
19!