
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Способы изменения внутренней энергии
Внутренняя энергия тела зависит от средней кинетической энергии его молекул, а эта энергия, в свою очередь, зависит от температуры. Поэтому, изменяя температуру тела, мы изменяем и его внутреннюю энергию.При нагревании тела его внутренняя энергия увеличивается, при охлаждении уменьшается.
Проделаем опыт. Укрепим на подставке тонкостенную латунную трубку. Нальем в нее немного эфира и плотно закроем пробкой. Теперь обовьем трубку веревкой и начнем натирать ею трубку, быстро вытягивая в веревку то в одну, то в другую сторону. Через В некоторое время внутренняя энергия трубки с эфиром возрастет настолько, что эфир закипит и образовавшийся пар вытолкнет пробку (рис. 60).

Этот опыт показывает, что внутреннюю энергию тела можно изменить путем совершения над телом работы, в частности трением.
Изменяя внутреннюю энергию куска дерева путем трения, наши предки добывали огонь. Температура воспламенения дерева равна 250 °С. Поэтому, чтобы получить огонь, нужно тереть одним куском дерева по другому до тех пор, пока их температура не достигнет этого значения. Легко ли это? Когда таким способом попробовали добыть огонь герои романа Жюля Верна "Таинственный остров", у них ничего не вышло.
"Если бы энергию, которую затратили Наб с Пенкрофом, можно было превратить в тепло, ее, наверное, хватило бы для отопления котла океанского парохода. Но результат их усилий равнялся нулю. Куски дерева, правда, разогрелись, но значительно меньше, чем сами участники этой операции.
После часа работы Пенкроф был весь в поту и с досадой отбросил куски дерева, сказав:
- Не говорите мне, что дикари добывают огонь таким образом! Я скорее поверю, что летом идет снег. Легче, пожалуй, зажечь собственные ладони, потирая их одну о другую".
Причина их неудачи заключалась в том, что огонь следовало добывать не простым трением одного куска дерева о другой, а сверлением дощечки заостренной палочкой (рис. 61). Тогда при определенной сноровке можно за 1 с увеличить температуру в гнезде палочки на 20 °С. А чтобы довести палочку до горения, потребуется всего лишь 250/20=12,5 секунды
20! Среди равновесных процессов, которые происходят с термодинамическими системами, отдельно рассматриваются изопроцессы, при которых один из основных параметров состояния остается постоянным.
Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.

Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:

т.к. CV=dUm/dt,

Тогда для произвольной массы газа получим
 (1)
(1)
Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V1 до V2 равна
 (2)
(2)
и равна площади заштрихованного прямоугольника (рис. 2). Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то
 и
и 
откуда

Тогда выражение (2) для работы изобарного расширения примет вид
 (3)
(3)
Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2 —T1 = 1К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.

Рис.1
В изобарном процессе при сообщении газу массой m количества теплоты

его внутренняя энергия возрастает на величину (т.к. CV=dUm/dt)

При этом газ совершит работу, определяемую выражением (3).
Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:

Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Исходя из формул для работы газа и уравнения Менделеева-Клайперона найдем работу изотермического расширения газа:

Так как при Т=const внутренняя энергия идеального газа не изменяется:
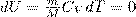
то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса

т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
 (4)
(4)
Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения.
21!Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством.  Серьёзное исследование адиабатических процессов началось в XVIII веке[1].
Серьёзное исследование адиабатических процессов началось в XVIII веке[1]. 
Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётсяравновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы[3].
Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона.  Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике.
Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике. 
22! 23 2
1. Испарение. Существует три агрегатных состояния вещества: твердое, жидкое и газообразное.
Переход вещества из жидкого состояния в газообразное называется парообразованием, а обратный переход – конденсацией.
Виды парообразования: испарение и кипение.
Испарение обусловлено хаотическим движением молекул и и происходит только со свободной поверхности, граничичащей с газообразной средой. Вылетая из жидкости, молекулы должны преодолеть силы притяжения, действующие со стороны других молекул, т.е. совершить работу выхода. Сделать это могут только быстрые молекулы. Таким образом, в жидкости остаются молекулы с малой кинетической энергией, поэтому жидкость при испарении охлаждается.
Испарение и конденсация всегда происходят одновременно, но один из этих процессов может преобладать. Скорость испарения зависит от:
– природы жидкости;
– температуры;
– площади свободной поверхности;
– плотности паров жидкости над поверхностью;
– внешнего давления.
Поскольку среднее расстояние между молекулами в жидком состоянии меньше, чем в газообразном, объем вещества при парообразовании увеличивается.
Парообразование сопровождается поглощением теплоты из окружающей среды. Теплота парообразования прямо пропорциональна массе вещества:

Удельная теплота парообразования измеряется количеством теплоты, необходимым для превращения в пар единицы массы жидкости.
[L] = Дж/кг.
С ростом температуры удельная теплота парообразования уменьшается.
2. Насыщенный пар. Если плотность пара над поверхностью жидкости велика, то конденсация может происходить с той же скоростью, что и испарение, т.е. число молекул, покидающих жидкость в единицу времени, равно числу молекул, возвращающихся в нее. В таком случае говорят, что пар находится в состоянии подвижного равновесия со своей жидкостью.
Пар, находящийся в подвижном равновесии со свей жидкостью, называется насыщенным.
Покажем, что насыщенный пар газовым законам не подчиняется. Пусть в цилиндре с поршнем находится ненасыщенный пар (рис. 6.1.A). При изотермическом сжатии давление и плотность увеличиваются до тех пор пока пар не приходит в состояние насыщения (рис. 6.1.B). При дальнейшем сжатии в цилиндре появляется жидкость, а давление пара остается постоянным (рис. 6.1.C). После того как весь пар превращается в жидкость, дальнейшее сжатие ведет к резкому скачку давления (рис. 6.1.D).

Рис. 6.1.
На рис. 6.2 показана зависимость давления от объема в данном опыте, и отмечены точки A, B, C и D, отражающие состояния пара, изображенные на рис. 6.1. Пока в цилиндре ненасыщенный пар, сжатие происходит по изотерме в соответствии законом Бойля–Мариотта (участок AB). При дальнейшем сжатии объем жидкости увеличивается, а давление остается постоянным (участок BD). Таким образом, давление насыщенного пара не зависит от объема.

Рис. 6.2.
Давление и плотность насыщенного пара увеличиваются с ростом температуры. Плотность насыщенного пара показывает какое максимальное количество пара может содержаться в единице объема при данной температуре.
Закон Дальтона:
Давление смеси паров и газов равно сумме давлений, создаваемых каждым из них в отдельности, если между ними нет химического взаимодействия.
Следствием закона Дальтона является утверждение: присутствие над поверхностью насыщенного пара одной жидкости не мешает испаряться другой.
3. Влажность воздуха.
Количество водяного пара, содержащегося в 1 м3 воздуха, называется абсолютной влажностью.
[  а ] = г/м3.
а ] = г/м3.
Относительная влажность воздуха это число, показывающее сколько процентов от плотности насыщенного пара при данной температуре составляет абсолютная влажность.

Температура, при которой воздух в процессе своего охлаждения становится насыщенным водяными парами, называется точкой росы.
[tр ] = °C
4. Критическое состояние вещества. С повышением температуры плотность насыщенного пара увеличивается, а плотность жидкости в результате теплового расширения уменьшается (рис. 6.3).

Рис. 6.3.
Температура, при которой плотность жидкости и плотность ее насыщенного пара становятся одинаковыми, называется критической.
При критической температуре различия между жидкостью и паром стираются. Вещество при этом находится в критическом состоянии, и параметры этого состояния называются критическими. Для воды, например, tкр = 374 °C, pкр = 219 атм,  кр = 329 кг/м3.
кр = 329 кг/м3.
5. Реальный газ.
График изотермического процесса для идеального газа в координатах p,V представляет гиперболу. Для реального же газа экспериментальная изотерма имеет горизонтальный участок (рис. 6.4).

Рис. 6.4.
Если состояние идеального газа описывается уравнением Клапейрона-Менделеева:
pV =  RT,
RT,
то для описания состояния реального газа следует использовать экспериментально полученное уравнение Ван-дер-Ваальса:

Параметры a и b в этом уравнении индивидуальны для каждого газа. Для воды, например, они равны:


Параметры a и b могут быть выражены через критические параметры газа:


здесь Vкр – объем 1 моля газа в критическом состоянии.
24! Жидкости занимают промежуточное положение между газообразными и твердыми веществами. При температурах, близких к температурам кипения, свойства жидкостей приближаются к свойствам газов; при температурах, близких к температурам плавления, свойства жидкостей приближаются к свойствам твердых веществ. Если для твердых веществ характерна строгая упорядоченность частиц, распространяющаяся на расстояния до сотен тысяч межатомных или межмолекулярных радиусов, то в жидком веществе обычно бывает не более нескольких десятков упорядоченных частиц - объясняется это тем, что упорядоченность между частицами в разных местах жидкого вещества так же быстро возникает, как и вновь «размывается» тепловым колебанием частиц. Вместе с тем общая плотность упаковки частиц жидкого вещества мало отличается от твердого вещества - поэтому их плотность близка к плотности твердых тел, а сжимаемость очень мала. Например, чтобы уменьшить объем, занимаемый жидкой водой, на 1%, требуется приложить давление ~ в 200 атм, тогда как для такого же уменьшения объема газов требуется давление порядка 0,01 атм. Следовательно, сжимаемость жидкостей примерно и 200 : 0,01 = 20000 раз меньше сжимаемости газов.
Выше отмечалось, что жидкости имеют определенный собственный объем и принимают форму сосуда, в котором находятся; эти их свойства значительно ближе к свойствам твердого, чем газообразного вещества. Большая близость жидкого состояния к твердому подтверждается также данными по стандартным энтальпиям испарения ∆Н°исп и стандартным энтальпиям плавления ∆Н°пл. Стандартной энтальпией испарения называют количество теплоты, необходимое для превращения 1 моль жидкости в пар при 1 атм (101,3 кПа) . То же количество теплоты выделяется при конденсации 1 моль пара в жидкость при 1 атм. Количество теплоты, расходуемое на превращение 1 моль твердого тела в жидкость при 1 атм, называют стандартной энтальпией плавления (то же количество теплоты высвобождается при «замерзании» («отвердевании» ) 1 моль жидкости при 1 атм) . Известно, что ∆Н°пл намного меньше соответствующих значений ∆Н°исп, что легко понять, поскольку переход из твердого состояния в жидкое сопровождается меньшим нарушением межмолекулярного притяжения, чем переход из жидкого в газообразное состояние.
Ряд других важных свойств жидкостей больше напоминает свойства газов. Так, подобно газам жидкости могут течь - это их свойство называется текучестью. Сопротивляемость течению определяется вязкостью. На текучесть и вязкость влияют силы притяжения между молекулами жидкости, их относительная молекулярная масса, а также целый ряд других факторов. Вязкость жидкостей ~ в 100 раз больше, чем у газов. Так же, как и газы, жидкости способны диффундировать, хотя и гораздо медленнее, поскольку частицы жидкости упакованы гораздо плотнее, чем частицы газа.
Одно из важнейших свойств именно жидкости - ее поверхностное натяжение (это свойство не присуще ни газам, ни твердым веществам) . На молекулу, находящуюся в жидкости, со всех сторон равномерно действуют межмолекулярные силы. Однако на поверхности жидкости баланс этих сил нарушается, и вследствие этого «поверхностные» молекулы оказываются под действием некой результирующей силы, направленной внутрь жидкости. По этой причине поверхность жидкости оказывается в состоянии натяжения. Поверхностное натяжение - это минимальная сила, сдерживающая движение частиц жидкости в глубину жидкости и тем самым удерживающая поверхность жидкости от сокращения. Именно поверхностным натяжением объясняется «каплевидная» форма свободно падающих частиц жидкости.
25!Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.
Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости[1].
Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности  — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
— сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
В 1983 году было доказано теоретически и подтверждено данными из справочников (посмотреть статью: Журнал физической химии. 1983, № 10, с. 2528—2530), что понятие поверхностного натяжения жидкости однозначно является частью понятиявнутренней энергии (хотя и специфической: для симметричных молекул близких по форме к шарообразным). Приведенные в этой журнальной статье формулы позволяют для некоторых веществ теоретически рассчитывать значения поверхностного натяжения жидкости по другим физико-химическим свойствам, например, по теплоте парообразования или по внутренней энергии (подробнее о физической природе поверхностного натяжения жидкости см.соотв. статью на викиучебнике или [2] , [3])
В 1985 году аналогичный взгляд на физическую природу поверхностного натяжения, как части внутренней энергии, при решении другой физической задачи был опубликован В. Вайскопфом (Victor Frederick Weisskopf) в США (V.F.Weisskopf, American Journal of Physics 53 (1985) 19-20.; V.F.Weisskopf, American Journal of Physics 53 (1985) 618—619.).
Поверхностное натяжение может быть на границе газообразных, жидких и твёрдых тел. Обычно имеется в виду поверхностное натяжение жидких тел на границе «жидкость — газ». В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.
В общем случае прибор для измерения поверхностного натяжения называется тензиометр.
26! Смачивание. Мениск. Давление создаваемое искривленной поверхностью жидкости. Капиллярные явления в быту. В природе, технике. Капилляры и их свойства.
Смачивание - это поверхностное явление, заключающееся во взаимодействии жидкости. Смачивание бывает двух видов:
- Иммерсионное (вся поверхность твёрдого тела контактирует с жидкостью)
- Контактное (состоит из трёх фаз — твердая, жидкая, газообразная)
Смачивание зависит от соотношения между силами сцепления молекул жидкости с молекулами смачиваемого тела и силами взаимного сцепления молекул жидкости.
Степень смачивания характеризуется углом смачивания. Угол смачивания (или краевой угол смачивания) это угол, образованный касательными плоскостями к межфазным поверхностям, ограничивающим смачивающую жидкость, а вершина угла лежит на линии раздела трёх фаз. Измеряется методом лежащей капли. В случае порошков надёжных методов, дающих высокую степень воспроизводимости, пока (по состоянию на 2008 год) не разработано. Предложен весовой метод определения степени смачивания, но он пока не стандартизован.
Мениск - искривлённая свободная поверхность жидкости в месте её соприкосновения с поверхностью твердого тела. Образуется у стенок сосудов, в каналах-порах губчатых тел, пропитанных жидкостью, и т.д.
В тонкой трубке (капилляре) мениск имеет сферическую форму, в достаточно узком зазоре между плоскими пластинами — цилиндрическую. Кривизна мениска определяется соотношением сил межмолекулярного взаимодействия на границе трёх фаз — твёрдого тела, жидкости и газа. Жидкость, смачивающая данную поверхность, образует вогнутый мениск, несмачивающая — выпуклый. В первом случае взаимное притяжение молекул жидкости слабее их притяжения молекулами поверхности твёрдого тела. Во втором, наоборот, силы когезии преобладают над силами адгезии. Давление паров над вогнутым мениском ниже, а над выпуклым выше, чем над плоской поверхностью жидкости.
Капилляры — физическое явление, заключающееся в способности жидкостей изменять уровень в трубках, узких каналах произвольной формы, пористых телах. Поднятие жидкости происходит в случаях смачивания каналов жидкостями, например воды в стеклянных трубках, песке, грунте и т. п. Понижение жидкости происходит в трубках и каналах, не смачиваемых жидкостью, например ртуть в стеклянной трубке.
На основе капиллярности основана жизнедеятельность животных и растений, химические технологии, бытовые явления (например, подъём керосина по фитилю в керосиновой лампе, вытирание рук полотенцем). Капиллярность почвы определяется скоростью, с которой вода поднимается в почве и зависит от размера промежутков между почвенными частицами.
27! Твёрдое тело — это одно из четырёх агрегатных состояний вещества, отличающееся от других агрегатных состояний (жидкости,газов, плазмы) стабильностью формы и характером теплового движения атомов, совершающих малые колебания около положений равновесия[1].
Различают кристаллические и аморфные твёрдые тела. Раздел физики, изучающий состав и внутреннюю структуру твёрдых тел, называется физикой твёрдого тела. То, как твёрдое тело меняет форму при воздействиях и движении, изучается отдельной дисциплиной — механикой твёрдого (деформируемого) тела. Движением абсолютно твёрдого тела занимается третья наука —кинематика твёрдого тела.
Технические приспособления, созданные человеком, используют различные свойства твёрдого тела. В прошлом твёрдое тело применялось как конструкционный материал и в основе употребления лежали непосредственно ощутимые механические свойства как то твёрдость, масса, пластичность, упругость, хрупкость. В современном мире применение твёрдого тела основывается на физических свойствах, которые зачастую обнаруживаются только при лабораторных исследованиях.
28!Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.
| Причины отказа механики |
| Прогиб |
| Коррозия |
| Пластическая деформация |
| Усталость материала |
| Удар |
| Трещина |
| Плавление |
| Износ |
| Шаблон: Просмотр • Обсуждение • Править |
Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия (другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (то есть выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).
Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.
29! 1.1. Кристаллические и аморфные тела.
Мы будем рассматривать в дальнейшем свойства только кристаллических тел, то есть свойства тел, образующих в твердом состоянии упорядоченную структуру. Реально переход тела из жидкой (или газообразной) фазы к твердое состояние не обязательно сопровождается кристаллизацией тела, а может приводить к аморфизации тела, в том числе и к образованию стеклообразного состояния, которое получается из вязкого расплава при быстром его охлаждении, т. е. твердением без кристаллизации.
При первом знакомстве с кристаллами прежде всего бросается в глаза их правильная многогранная форма. Этот образ кристалла в виде правильного многогранника возник у нас от драгоценных камней, природных минералок и искусственных кристаллов. Прозрачный кварц и красный рубин, мягкий тальк и сверхтвердый алмаз, микроскопические крупинки сахарного песка и гигантские сталактиты — вот лишь некоторые представители удивительно многообразного царства кристаллов. На рис. 1.1.1 приведена фотография друзы горного хрусталя.
 Такие кристаллы часто называют монокристаллами, чтобы отличить их от поликристаллов — конгломерата микроскопических кристалликов, которыми является большинство минералов и металлов. Как правило, нас будут интересовать физические свойства монокристаллов, так как свойства поликристаллов определяются не только свойствами самих микроскопических кристалликов, а во многом их взаимным расположением и способом соединения
Такие кристаллы часто называют монокристаллами, чтобы отличить их от поликристаллов — конгломерата микроскопических кристалликов, которыми является большинство минералов и металлов. Как правило, нас будут интересовать физические свойства монокристаллов, так как свойства поликристаллов определяются не только свойствами самих микроскопических кристалликов, а во многом их взаимным расположением и способом соединения
Рис. 1.1.1
Многие выращивали в школьные годы из водных растворов квасцов большие октаэдры кристаллов, поражающие своей геометрической правильностью. Монокристалл может иметь и кубическую форму, как кристалл поваренной соли, форму ромбической призмы, как кристалл сегнетовой соли, октаэдра или плоского треугольника, как кристалл титаната бария. Его форма может быть и более сложной комбинацией простых геометрических фигур, но это — его естественная форма. Таким его сотворила природа.
Естественно возникает вопрос, почему форма кристаллов так геометрически совершенна? Ответ был дан уже в конце XVI в. И. Кеплером и Р. Гуком. Правильную форму кристаллов поваренной соли и квасцов они объясняли тем, что эти кристаллы состоят из плотно упакованных частичек сферической формы. Идея решетчатого строения кристаллов буквально «носилась в воздухе», однако высказана она была впервые в конце XVII в. французским кристаллографом Р. Аюи.
Вот какая легенда дошла до нас о счастливом случае, натолкнувшем Аюи на мысль о внутреннем решетчатом строении кристаллов.
Однажды, находясь в гостях у знакомого любителя и собирателя минералов, Агои взял в руки и рассматривал друзу призматических кристаллов кальцита. По оплошности Аюи друза упала на пол и разбилась, причем кристаллы раскололись на несколько кусков правильной ромбоэдрической формы. Дома Аюи расколол все кристаллы кальцита из собственной коллекции. Несмотря на то, что эти кристаллы обладали самой разнообразной формой и в ряде случаев вовсе не имели в своем облике граней ромбоэдра, у осколков наблюдались только эти грани. Осколки, в свою очередь, раскалывались на все более а более мелкие ромбоэдры. "Увидев это, Аюи будто бы воскликнул: «Все найдено!»
Преимущественное раскалывание кристаллов по некоторым плоскостям, называемым плоскостями спайности, было известно давно. Однако только Аюи понял, что такое раскалывание кристалла, будучи продолжено достаточно большое число раз, приведет к получению предельно малых многогранных частичек, которые уже нельзя будет расколоть без нарушения природы их вещества. Из этих частичек, как из кирпичиков, строится кристалл, вырастая в природных или искусственных условиях. Эти кирпачики образуют как бы бесконечную (учитывая их малость по сравнению с макроскопическим кристаллом) пространственную решетку.
Умозрительная, хотя и основанная на наблюдении реально существующего явления — спайности, — теория решетчатого строения кристаллов Аюи только через 130 лет получила свое экспериментальное подтверждение. В 1912 г. немецкие физики А. Лауэ, В. Фридрих и П. Книнпинг обнаружили дифракцию рентгеновских лучей в кристаллах. Поскольку рентгеновское излучение имеет электромагнитную природу, то их дифракция может происходить только па пространственной решетке кристалла, т. е. на цепочках атомов или ионов, расстояния между которыми сравнимы с длиной волны рентгеновского излучения. Реальность пространственной структуры была доказана.
Современные экспериментальные методы дают возможность «непосредственно увидеть» расположение атомов кристалла в пространстве. На рис. 1.1.2 и 1.1.3 показано, как выглядит кристалл вольфрама в ионном микроскопе и решетка висмута в туннельном микроскопе.
28,8 А

Рис. 1.1.2 Рис. 1.1.3
Принципиальными особенностями кристаллических тел являются их трансляционная симметрия, то есть тот факт, что в кристаллах их структура (пространственное расположение ее элементов) полностью повторяется через определенное расстояние, называемое периодом решетки.
Принято говорить, что в отличие от дальнего порядка, наблюдаемого в кристаллах (упорядоченное расположение частиц в узлах кристаллической решетки сохраняется по всему объему кристалла), в жидкостях и аморфных телах имеет место ближний порядок в расположении частиц. Это означает, что по отношению к любой частице расположение ближайших соседей является упорядоченным, хотя и не так четко, как в кристалле, но по мере удаления от данной частицы расположение по отношению к ней других частиц становится все менее упорядоченным и довольно быстро (на расстоянии 3-4 эффективных диаметров молекулы) порядок в расположении частиц полностью исчезает.
Ошибочным является представление, что переход вещества из жидкого состояния в твердое означает сближение молекул, которое сопровождается увеличением сил сцепления между ними, а это и создает «твердость» вещества. Дело в том, что некоторые вещества (вода, висмут, сурьма) при кристаллизации увеличиваются в объеме, следовательно средние расстояния между соседними молекулами у этих веществ будут в твердой фазе больше, чем в жидкой, хотя, безусловно, в твердой фазе молекулы будут прочнее связаны между собой. Исходя из этого можно утверждать, что решающим фактором в процессе отвердевания кристаллических тел является не уменьшение расстояния между соседними частицами, а ограничение свободы их теплового движения. Само же ограничение обусловлено увеличением сил связи между частицами, которое возникает при упорядоченном расположении их в кристалле.
Итак, причиной геометрически правильной внешней формы кристалла является геометрически правильное внутреннее его строение — пространственная решетка. Пространственная решетка— это, конечно, абстракция. Просто в пространстве, которое занимает кристалл, наблюдается правильное, закономерное чередование атомов или ионов. Если их соединить воображаемыми прямыми, то получим пространственную решетку, в узлах которой располагаются атомы или ионы.
Рис. 1.1.4
 Для наглядности рассмотрим простой пример — кристалл хлористого натрия (поваренной соли) — см. рис. 1.1.4. Структура этого кристалла представляет собой кубическую решетку, где каждый ион Na+ окружен шестью ионами Сl- на расстоянии 2,81 Ǻ и, в свою очередь, каждый ион С1- окружен шестью ионами Na+. Поэтому ясно, что если кристалл хлористого натрия выращивается в равновесных условиях, то при наслаивании одной сетки чередующихся ионов Na+и Сl- на другую образуется монокристалл кубической внешней формы. Это очевидный пример. В других случаях, когда пространственные решетки более сложны, внешнюю форму кристаллов угадать не легко. Но есть общее свойство, которое однозначно показывает, как пространственная решетка определяет макроскопическую форму кристалла, и это свойство — симметрия.
Для наглядности рассмотрим простой пример — кристалл хлористого натрия (поваренной соли) — см. рис. 1.1.4. Структура этого кристалла представляет собой кубическую решетку, где каждый ион Na+ окружен шестью ионами Сl- на расстоянии 2,81 Ǻ и, в свою очередь, каждый ион С1- окружен шестью ионами Na+. Поэтому ясно, что если кристалл хлористого натрия выращивается в равновесных условиях, то при наслаивании одной сетки чередующихся ионов Na+и Сl- на другую образуется монокристалл кубической внешней формы. Это очевидный пример. В других случаях, когда пространственные решетки более сложны, внешнюю форму кристаллов угадать не легко. Но есть общее свойство, которое однозначно показывает, как пространственная решетка определяет макроскопическую форму кристалла, и это свойство — симметрия.
Симметрия «правит» миром кристаллов. Это общее свойство, определяющее законы расположения структурных элементов в пространственной решетке, взаимное расположение граней макроскопического кристалла, диктующее, какими физическими свойствами может обладать кристалл и по каким пространственным направлениям в нем эти свойства проявляются. Свойство симметрии является проявлением общих фундаментальных законов природы. Вообще под симметрией следует понимать способность фигуры закономерно повторять в себе свои части.
Например, при повороте куба вокруг трех прямых, мысленно проведенных через центры противоположных граней, он будет повторять себя через каждые 90° (см. рис. 1.1.4). Другой пример — прямоугольный параллелепипед. Если мы разделим era мысленно плоскостями, проходящими через середины ребер, и отразим фигуру относительно этих плоскостей, то увидим, что фигура совместилась сама с собой.
Симметрия внешней формы кристалла является проявлением геометрически правильного, симметричного расположения атомов и ионов. Симметрия кристалла кубической формы проявляется в том, что при повороте его вокруг оси, соединяющей центры противоположных граней, он совмещается сам с собой. Теперь вернемся к кубической решетке. Считая ее бесконечной (еще раз отметим, что в макроскопических масштабах мы имеем дело с громадным числом элементов кристалла; если ребро куба равно 1 см, то оно состоит примерно из 3 - 107 ионов!), проведем прямые через любую цепочку чередующихся ионов Na+ и С1- в том месте, где они расположены особенно близко друг к другу. Тогда при повороте решетки вокруг любой из прямых на 90° получаем решетку совершенно идентичную первоначальной.
Однако нетрудно сообразить, что в кристалле конечных размеров в каждом направлении расположена одна такая ось, а в бесконечной пространственной решетке имеется бесконечное число таких параллельных прямых.
Это очень важный вопрос, и связан он с основным признаком пространственной решетки — ее бесконечностью. Как мысленно можно построить бесконечную пространственную решетку? Выберем в любом месте пространства начало координат и поместим в эту точку, для простоты, атом или ион. Теперь из начала координат проведем три взаимно перпендикулярных вектора (в общем случае они могут иметь любое направление), длина каждого из которых равна расстояниям до ближайших атомов или ионов того же сорта, что и помещенный в начало координат. Эти три вектора, называемые векторами трансляции, позволяют построить бесконечную пространственную решетку. Для этого надо просто переносить все атомы или ионы решетки из первоначального положения на расстояния, равные трансляциям по их направлениям в пространстве.
Обозначим векторы трансляции а, Ь, с. Параллелепипед, имеющий в качестве ребер векторы а, Ь, с, называется примитивной ячейкой. Посредством соответствующих операций трансляций с помощью примитивной ячейки можно заполнить все пространство кристаллической структуры. Вообще говоря, можно выбрать бесконечное число элементарных ячеек, путем трансляции которых получается кристаллическая структура, но примитивная ячейка является элементарной ячейкой минимального объема.
Существует много таких физических явлений, в которых атомная структура вещества не проявляется непосредственным образом. При изучении этих явлений вещество можно рассматривать как сплошную среду, отвлекаясь от его внутренней структуры. Таковы, например, тепловое расширение тел, их деформация под влиянием внешних сил, диэлектрическая проницаемость, оптические свойства и т. п. Свойства вещества как сплошной среды называют макроскопическими свойствами.
Макроскопические свойства кристалла различны по разным направлениям в нем. Например, особенности прохождения света через кристалл зависят от направления луча; тепловое расширение кристалла происходит, вообще говоря, различно по разным направлениям; деформация кристалла зависит от ориентации внешних сил и т. п. Происхождение этой зависимости свойств от направления связано, конечно, со структурой кристалла. Так, например, растяжение кубического кристалла вдоль направления, параллельного ребрам кубических ячеек его решетки, будет происходить не так, как при растяжении вдоль диагонали этих ячеек, ибо энергия связи между атомами зависит от расстояния между ними.
Зависимость физических свойств тела от направления называется анизотропией. Анизотропия является характерной особенностью кристаллов, и в этом отношении они принципиально отличаются от изотропных сред — жидкостей и газов, — свойства которых одинаковы по всем направлениям.
Естественно, что кристалл выступает как однородная, непрерывная и анизотропная среда только по отношению к своим макроскопическим свойствам, но эти макроскопические свойства, в конце концов, определяются силами, действующими между структурными элементами пространственной решетки, а, следовательно, природой самих ионов, атомов или молекул, из которых построен кристалл. Этим же определяются и законы повторяемости структурных элементов пространственной решетки, ее симметрия. Это значит, что все физические свойства макроскопического кристалла связаны с его симметрией.
Каковы же элементы симметрии пространственной фигуры? Это воображаемые геометрические образы: точки, прямые и плоскости, относительно которых однообразно располагаются части фигур. Наличие плоскости симметрии свидетельствует о том, что одна часть фигуры совместится с другой, если перенести все ее точки по другую сторону плоскости по перпендикулярам к ней на равные расстояния. В таком случае говорят также, что это соответствует зеркальной симметрии фигуры.
Зеркальная симметрия, или симметрия левого и правого, широко распространена в природе. Почти одновременно понятие симметрии возникло в архитектуре и скульптуре как синоним гармоничности и красоты. Даже без строгих определений каждый скажет, что тело человека обладает зеркальной симметрией. На рис. 1.1.5 изображен рисунок Леонардо да Винчи, иллюстрирующий зеркальную симметрию человеческого тела. Зеркальной симметрией обладают листья деревьев и трав, насекомые, птицы и звери.
Ось симметрии — это прямая, при повороте вокруг которой на определенный угол фигура или части фигуры совмещаются сами с собой. Порядок оси или число совмещений при повороте на 360° определяется выражением

 (1.1)
(1.1)
где α — угол наименьшего поворота, приводящего фигуру в совмещение. Порядок оси —-целое число, и потому возможны следующие оси симметрии: ось первого порядка (n = 1), это естественно возможно для любой фибуры( ибо при повороре на α = 360° фигура совмещается сама с собий, второго (α = 180°), третьего (α 9 120°) и т.д. На рис. 1.1.6 изображены составленные из тетраэдров геометрические фигуры, иллюстрирующие различные законы их симметрии. На рис. 1.1.6 а показаны четыре одинаковых тетраэдра, в их расположении нет закономерности. Но эти тетраэдры можно расположить так, что получатся фигуры с осями 2, 3 и 4 порядка, приведенные на рис. 1.1.6 в, г, д. На рис. 7.6 6 показана фигура, составленная из таких же тетраэдров, но обладающая плоскостью симметрии. На рисунке эта плоскость проходит через ось CD, Рис. 1.1.5, 1.1.6
при отражении в этой плоскости вершины левого тетраэдра А и В переходят в вершины А' и В' правого тетраэдра.
Элементы симметрии не исчерпываются только плоскостью и поворотными осями симметрии. Представим себе, что два тетраэдра связаны как бы осью симметрии второго порядка, но при этом их вершины направлены в противоположные стороны (см. рис. 1.1.6 е). Как понять такую операцию? В принципе это очень просто. Имеется особая точка (ее называют центр инверсии, или центр симметрии) — общая вершина двух тетраэдров, — отражением в которой фигура совмещается сама с собой.
Материальные фигуры и тем более кристаллы обладают, как правило, не одним элементом симметрии. Вот, например, книга: у нее кроме оси второго порядка есть еще две плоскости симметрии, проходящие через эту ось. Кроме того, как и всякая фигура, книга преобразуется в себя при повороте на 360°, т. е. у нее присутствует ось первого порядка.
Полный набор элементов симметрии какой-либо материальной фигуры называется группой (видом) симметрии этой фигуры. Почему для физики особое значение имеют группы симметрии? Оказывается, что именно они чаще всего определяют то или иное физическое явление в кристаллах.
1.2. Типы кристаллических решеток
В основе кристаллической решетки лежит элементарная кристаллографическая ячейка, представляющая собой параллелепипед с характерным для данной решетки расположением атомов.
Важнейшим геометрическим свойством кристаллов, кристаллических решеток и их элементарных ячеек является, как мы уже обсуждали в предыдущем параграфе, симметрия по отношению к определенным направлениям (осям) и плоскостям. Число возможных видов симметрии ограничено. Французский кристаллограф О. Браве в 1848 г. положил начало геометрической теории структуры кристаллов и показал, что в зависимости от соотношения величин и взаимной ориентации ребер элементарной кристаллической ячейки может существовать 14 типов кристаллических решеток, которые получили название решеток Браве.
Различают примитивные (простые), базоцентрированные, объемноцентрированные и гранецентрированные решетки Браве. Если узлы кристаллической решетки расположены только в вершинах параллелепипеда, представляющего собой элементарную ячейку, то такая решетка называется примитивной или простой. Если же, кроме того, имеются узлы в центре основания параллелепипеда, то решетка называется базоцентрированной, если есть узел в месте пересечения пространственных диагоналей — решетка называется объемноцентрированной, а если имеются узлы в центре всех боковых граней — гранецентрированной.
Почти половина всех элементов образует кристаллы кубической или гексагональной симметрии, которые мы рассмотрим подробно. В кристаллах кубической системы возможны три решетки: простая, объемноцентрированная и гранецентрированная. В кубической системе все углы элементарной ячейки прямые и все ребра ее равны между собой. Элементарная ячейка гексагональной системы представляет собой прямую призму, в основании которой лежит ромб с углами 60 и 120°. Два угла между осями ячейки прямые, а один равен 120°.
Во многих случаях можно считать, что кристалл представляет собой систему из соприкасающихся твердых шаров. Минимуму энергии будет соответствовать такая структура, в которой шары наиболее плотно упакованы. Плотность упаковки или коэффициент компактности определяется отношением объема частиц к объему элементарной ячейки, Уа. В случае частиц одного сорта кратчайший период а и соотношение между радиусом шаров R и а определяет контакт между соседними шарами.
Сравним между собой в такой модели три возможных кубических структуры.
1. Простая кубическая ячейка, когда атомы находятся лишь в узлах куба: в этом случае на одну примитивную ячейку приходится один атом.
2. Гранецентрированная кубическая решетка {г. ц. к.): атомы находятся не только в узлах, но и посредине шести граней; такую структуру имеет, например, хлористый натрий.
3. Объемноцентрированная кубическая решетка (о, ц. к.): атомы находятся в узлах куба, и, кроме того, один в его центре.
Наиболее «рыхлой» оказывается структура простого куба, и химические элементы «предпочитают» не кристаллизоваться в такие структуры, хотя многие вещества в кристаллическом состоянии обладают структурой простого куба — например, CsCl, CuPd, BeCu, LiHg. Наибольшей компактностью обладает г. ц. к. структура, поэтому ее называют также кубической структурой с плотной упаковкой. Однако расположить одинаковые твердые шары в пространстве так, чтобы остающийся между ними объем был минимален, можно и другим способом — образуя гексагональную плотную упаковку (г. п. у.), причем в этой структуре плотность упаковки оказывается равной 0,74, как и в г. ц. к.
7.3.  Поэтому многие металлы при определенных температурах довольно легко изменяют свою структуру с гранецентрированной кубической на структуру с гексагональной плотной упаковкой и наоборот. Каркас такой ячейки имеет гексагональное основание, соответствующее плотной упаковке твердых шаров (как мячей на столе). Следующая атомная плоскость упакована аналогично, но сдвинута так, что ее атомы располагаются между атомами первой плоскости; третья плоскость упакована так же, и ее атомы лежат в точности над атомами первой плоскости; четвертая плоскость расположена аналогично второй и т. д. На рис. 1.1.8, показаны три простейшие кристаллические решетки — объемноцентрированный куб {о. ц. к.), гранецентрированный куб {г. ц. к.), гексагональная структура плотной упаковки (г. п. у.) и их схематические представления. Рис. 1.1.8
Поэтому многие металлы при определенных температурах довольно легко изменяют свою структуру с гранецентрированной кубической на структуру с гексагональной плотной упаковкой и наоборот. Каркас такой ячейки имеет гексагональное основание, соответствующее плотной упаковке твердых шаров (как мячей на столе). Следующая атомная плоскость упакована аналогично, но сдвинута так, что ее атомы располагаются между атомами первой плоскости; третья плоскость упакована так же, и ее атомы лежат в точности над атомами первой плоскости; четвертая плоскость расположена аналогично второй и т. д. На рис. 1.1.8, показаны три простейшие кристаллические решетки — объемноцентрированный куб {о. ц. к.), гранецентрированный куб {г. ц. к.), гексагональная структура плотной упаковки (г. п. у.) и их схематические представления. Рис. 1.1.8
Типы связей в кристаллах
Классификация кристаллов по кристаллическим системам дает представление о геометрических характеристиках кристалла, но не затрагивает вопроса о природе сил, удерживающих атомы (молекулы или ионы) в определенных местах друг относительно друга — в узлах кристаллической  решетки. Классификацию кристаллов можно провести по другому принципу — в зависимости от физической природы сил, действующих между частицами кристалла. В таком случае мы получаем четыре типа кристаллов (и кристаллических решеток): ионные, атомные, металлические и молекулярные. Фактически, рассматривая кристаллы с этой точки зрения, мы ищем структуру основного состояния.
решетки. Классификацию кристаллов можно провести по другому принципу — в зависимости от физической природы сил, действующих между частицами кристалла. В таком случае мы получаем четыре типа кристаллов (и кристаллических решеток): ионные, атомные, металлические и молекулярные. Фактически, рассматривая кристаллы с этой точки зрения, мы ищем структуру основного состояния.
Атомные кристаллы. В узлах кристаллической решетки атомных кристаллов находятся атомы того или другого вещества. Атомные или го-меополярные кристаллы образуются при наличии так называемой гомеопо-лярной или ковалентной связи. Такая связь есть результат квантовомеха-нического обменного взаимодействия, которое подробно разбиралось раньше на примере молекулы водорода. Ковалентная химическая связь возникав!' между двумя атомами за счет образования общей пары валентных электронов по одному от каждого атома. За счет ковалентных связей образуются кристаллы углерода (алмаз), кремния, германия, серого олова. Гомеопо-лярная связь бывает не только между одинаковыми атомами, но и между атомами различных элементов — например, карбид кремния SiC, нитрид алюминия A1N
Ковалентная связь образуется в том направлении, в котором расположена наибольшая часть электронного облака обобществленных электронов. Это означает, что такая связь имеет направленный характер и под влиянием го-меополярной связи атомы не только устанавливаются на определенных расстояниях друг от друга, но и образуют определенные пространственные конфигурации. Ковалентная химическая связь очень прочна, поэтому атомные кристаллы отличаются высокой температурой плавления, большой твердостью и малой летучестью.
Ионные кристаллы. В узлах кристаллической решетки ионных кристаллов находятся ионы. Ионы располагаются так, что силы кулоновского притяжения между ионами противоположного знака больше, чем силы отталкивания между ионами одного знака. Таким образом, ионная связь (она также называется полярной, гетерополярной) обусловлена преимущественно электростатическим взаимодействием противоположно заряженных ионов. Ионная связь является типичной для неорганических соединений. Силы электростатического притяжения и отталкивания между ионами обладают сферической симметрией, и поэтому ионы разных знаков ведут себя подобно твердым шарам, притягивающимся друг к другу.
Возникает естественный вопрос: почему многие атомы легко присоединяют электрон и становятся электроотрицательными ионами (как, например, хлор)? Казалось бы, у нейтрального атома нет сил кулоновского взаимодействия с электроном. На самом деле, действительно, взаимодействие нейтрального атома с электроном не является следствием статического притяжения. Электрон наводит в атоме электрический днпольный момент, в результате чего возникает потенциал притяжения, пропорциональный 1/г* и действующий на больших расстояниях. Во многих случаях этот поляризационный потенциал притяжения достаточно велик для того, чтобы свободный атом смог присоединить добавочный электрон.
Число ионов противоположного знака, которое составляет ближайшее окружение данного иона в кристалле, называется координационным числом К. Значение координационного числа определяется величиной отношения радиусов ионов противоположного знака гл/гд. Чем ближе это отношение к единице, тем больше К. Так, например, при равенстве ионных радиусов (гл = гд) К = 12, при гд/гв < 0,22 координационное число К — 2.
Достаточно хорошей моделью ионных кристаллов является модель твердых шаров. Это связано с тем, что степень ионизации атомов, составляющих ионный кристалл, часто такова, что электронные оболочки всех ионов соответствуют электронным оболочкам, характерным для атомов инертных газов. Так, например, электронная оболочка иона Na+ подобна Ne, иона С1~ — Аг, и тем самым ионный кристалл состоит как бы из сферических заряженных атомов. Поэтому тип решетки ионных кристаллов практически определяется соотношением ионных радиусов. Например, кристаллы хлористого натрия имеют структуру граненентрированной кубической решетки вследствие того, что размер иона хлора (1,81 А) почти вдвое превышает размер иона натрия (0,98 А); при таком соотношении ионных радиусов в центре кубической ячейки хлористого натрия свободное пространство оказывается недостаточным для размещения еще одного иона и образования объсмноцен-трированной ячейки. Иначе обстоит дело с кристаллом хлористого цезия. Размеры ионов хлора и цезия близки (1,81 и 1,65 А), пространство и центре элементарного куба оказывается достаточным для размещения еще одного иона, и энергетически выгоднее оказывается более плотно упакованная структура — объемноцептрированный куб.
Металлические кристаллы. Как и в ковалептных кристаллах, в узлах пространственной решетки металлических кристаллов размещаются совершенно одинаковые частицы (для простоты рассуждений мы будем рассматривать чистые металлы, а не сплавы). При конденсации паров металла в жидкое или твердое состояние его атомы сближаются столь близко, что волновые функции валентных электронов существенно перекрываются и становятся «общими» для всего объема металла. Поэтому валентные электроны п металлах принято называть обобществленными или коллективизированными. Можно говорить в таком случае, что внутри металлического кристалла имеется свободный электронный газ. Электроны связывают положительные ионы металла в прочную систему.
Если исходить из модели плотной упаковки шаров, то можно определить атомный радиус элемента как половину расстояния между соседними атомами. Атомный радиус металла значительно больше его ионного радиуса в каком-либо соединении. Например, радиус иона натрия в кристаллах поваренной соли равен 0,98 А, а его атомный радиус в кристалле металлического натрия — 1,89 А. Это говорит о том, что одноименно заряженные ионы металла в металлическом кристалле не могут сближаться так же тесно, как разноименные ионы в ионных соединениях.
Если предположить, что ионы металла имеют сферическую форму, то можно полагать, что структура таких кристаллов должна соответствовать плотной упаковке шаров одинакового размера — гранецентрированному или объемно центрированному кубу, либо гексагональной решетке. Ближе всего к идеальной плотноупаковашюй гексагональной решетке подходит решетка магния. Молекулярные кристаллы. В узлах кристаллической решетки таких кристаллов находятся устойчивые молекулы, которые сохраняют индивидуальность не только в газообразной, но и в жидкой и твердой фазах (На, N2, Cfo, Bra, CH, CC>2, H2O}. Молекулы удерживаются в узлах решетки довольно слабыми вандерваальсовскими силами, природа которых сводится к взаимодействию между молекулярными диполями.
Различают три вида взаимодействия молекул, связанных силами Ван-дер-Ваал ьса.
1. Если молекулы данного вещества являются электрическими диполями, то силы электростатического взаимодействия между ними будут стремиться расположить молекулы в определенном порядке, которому соответствует минимум потенциальной энергии. Такой тип взаимодействия полярных молекул, зависящий от их ориентации, называется ориентационным.
2. Неполярные молекулы некоторых веществ обладают высокой поляризуемостью, поэтому под влиянием внешнего электрического поля (например, при приближении полярной молекулы) у таких молекул возникает наведенный (индуцированный) электрический момент. При сближении такие индуцированные диполи будут взаимодействовать друг с другом аналогично взаимодействию жестких диполей. Такое взаимодействие называют индукционным или поляризационным.
3. Возможен и так называемый дисперсионный вид взаимодействия. Это динамическое по своей природе взаимодействие является результатом того, что атом (молекула) обладает вследствие движения электронов переменным по величине и направлению дипольным моментом, равным произведению заряда электрона на радиус его орбиты. Энергетически оказывается более выгодной такая конфигурация соседних атомов, когда мгновенные значения дипольных моментов соседних атомов совпадают по направлению, что приводит к возникновению притяжения между ними.
Силы Ван-дер-Ваальса являются более короткодействующими, чем ку-лоновские силы. Кулоновские силы пропорциональны г , а вандервааль-ские — ~ г~6. Эта зависимость легко получается из рассмотрения поляризационного взаимодействия, когда статический диполь с моментом р] наводит дипольный момент р2 = 2ар|/т-3. Так как pi || р2, то потенциальная энергия равна
U(г) = -2Р1р2/г3 - 4ар?/г6. (7.2)
Силы Ван-дер-Ваальса всегда слабы, поэтому молекулярные связи четко проявляются лишь в тех случаях, когда они возникают между нейтральными атомами или молекулами. Многие органические соединения (парафиновые цепи и жирные кислоты) образуют молекулярные кристаллы.
Одним из видов межмолекулярного взаимодействия является и водородная связь. Водородная связь между молекулами осуществляется атомом водорода, который, будучи химически связан с одной молекулой (например, через гидроксил), одновременно взаимодействует с атомом кислорода другой молекулы. Соединения с водородной связью обладают тенденцией к полимеризации. Существенную роль водородная связь играет во взаимодействии молекул воды, побуждая их ассоциироваться в группы из двух, четырех или восьми молекул, что обусловливает аномальные физические Конечно, классификация кристаллов по типам связи достаточно условна, ибо в ряде случаев трудно отнести с определенностью кристаллы лишь к тому или иному классу. Но, тем не менее, приближенная классификация оказывается во многих случаях очень полезна, так как она позволяет выявить физическую природу сил, а значит и свойства образующихся структур.
7.4. Жидкие кристаллы
Большинство веществ может находиться только в трех агрегатных состояниях: твердом, жидком или газообразном. Однако некоторые органические вещества, обладающие сложными молекулами, могут образовывать четвертое, жидкокристаллическое. Как следует из самого названия, речь идет о специфическом агрегатном состоянии вещества, в котором оно проявляет одновременно свойства кристалла и жидкости. Оказывается, что при плавлении кристаллов этих веществ образуется жидкокристаллическая фаза, отличающаяся от обычных жидкостей. Эта фаза существует в интервале от температуры плавления до некоторой более высокой температуры, при нагреве до которой жидкий кристалл переходит в обычную жидкость.
Первым, кто обнаружил жидкие кристаллы, т. е. понял, что это самостоятельное агрегатное состояние вещества, был австрийский ученый, ботаник Рейнитцер. Исследуя новое синтезированное им вещество холестерилбензо-ат, он в 1888 г. обнаружил, что при нагреве до температуры 145 °С кристаллы этого вещества плавятся, образуя мутную, сильно рассеивающую свет жидкость. Затем по достижении температуры 179 °С жидкость становится прозрачной, т. е. начинает себя вести в оптическом отношении как обычная жидкость, например вода. Неожиданные свойства холестерилбензоат обнаруживал в мутной фазе. Рассматривая его под поляризационным микроскопом, Рейнитцер обнаружил, что в этой фазе он обладает двулучепреломлением. Это означает, что показатель преломления этой фазы зависит от поляризации света. Но явление двупреломлсния — это типично кристаллический эффект, и в изотропной жидкости он не должен наблюдаться.
Более детальные исследования, к которым Рейнитцер привлек известного физика Лемана, показали, что наблюдаемый эффект не может быть обусловлен двухфазностью этого состояния, т. е. мутная фаза полностью однородна, она не является жидкостью, в которой содержатся кристаллиты. Это фазовое состояние и было названо Лсманом жидкокристаллическим.
Подобно обычным жидкостям, жидкие кристаллы текучи и принимают форму сосуда, в котором помещены. А с другой стороны, образующие их молекулы упорядочены в пространстве. Правда, это упорядочение не такое полное, как в обычных кристаллах. Пространственная ориентация молекул жидких кристаллов состоит в том, например, что все длинные оси молекул одинаково ориентированы. Для характеристики ориентационного порядка вводится вектор единичной длины L, называемый директором, направление которого совпадает с направлением усредненной ориентации длинных осей молекул. Кроме того, вводится еще одна величина, параметр порядка 5, который характеризует степень ориентационного упорядочения молекул. Параметр порядка определяется следующим образом:
5=(3/2)(со?ё-1/3), (7.3)
где 9 — угол между направлениями директора и мгновенным направлением длинной оси молекул, a cos2 в означает среднее по времени значение cos2 в.
ГЛ. 7, Кристаллические структуры твердых тел
Из этой формулы ясно, что параметр 5" может принимать значения от О до 1. Значение 5=1 соответствует полной ориентациопной упорядоченности, a S — 0 означает полный ориентационный беспорядок и соответствует переходу жидкого кристалла в изотропную жидкость.
В зависимости от характера упорядочения осей молекул жидкие кристаллы разделяются на три разновидности: нематические, смектические и хо-лестерические.
Нематики. Чтобы схематично описать устройство нематиков, удобно молекулы, образующие его, представить в виде палочек. Для такой идеализации есть физические основания. Молекулы жидких кристаллов представляют собой типичные для многих органических веществ образования со сравнительно большим молекулярным весом, порядка сотни, сильно вытянутые в одном направлении. Структура типичного нематика приведена на рис. 7.9 а. При наблюдении нематика через микроскоп видна причудлиэая совокупность пересекающихся линий, или, как их называют, нитей, представляющих собой границы раздела между однодоменными областями. Отсюда и произошло название «нематик» — по-гречески «нема» означает «нить».
t \
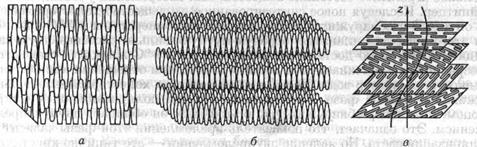
Рис. 7.9
При введенной нами идеализации структуру нематика следует представлять как «жидкость одинаково ориентированных палочек». Это означает, что центры тяжести расположены и движутся хаотически, как в жидкости, а ориентация всех осей при этом остается одинаковой и неизменной.
На самом деле, конечно, молекулы нематика совершают не только случайные поступательные движения, но также и ориентациониые колебания. Поэтому палочки задают преимущественную, усредненную ориентацию. Амплитуда ориентациоиных колебаний молекул зависит от близости жидкого кристалла к точке фазового перехода в обычную жидкость, возрастая по мере приближения температуры нематика к температуре фазового перехода. В точке фазового перехода ориентационное упорядочение молекул исчезает, и ориентация молекул становится полностью хаотической.
Смектики. В смектических жидких кристаллах степень упорядочения молекул выше, чем в нематиках. Схематически структура смектика выглядит так, как это показано на рис. 7.9 б. В смектиках, помимо ориентационной упорядоченности молекул, аналогичной случаю нематиков, существует частичное упорядочение центров тяжести молекул — молекулы смектика организованы в слои, расстояния между которыми фиксированы, что и дает упорядочение слоев. Ориентация молекул в слое может быть как перпендикулярна плоскости слоя, так и направлена под некоторым углом к нему.
Общим для всех смектиков, независимо от описанных выше деталей их структуры, является слабое взаимодействие молекул, принадлежащих к различным слоям, по сравнению с взаимодействием молекул внутри одного слоя. По этой причине слои легко скользят друг относительно друга и смектики на ощупь мылоподобны. Отсюда и их название, в основе которого лежит греческое слово «смегма», что значит мыло. Аналогично нематикам, смектики обладают двулуч
Дата добавления: 2015-01-19; просмотров: 340; Мы поможем в написании вашей работы!; Нарушение авторских прав |