Весовые коэффициенты важности критериев

При появлении многокритериальных задач возникли дополнительные трудности их решения, связанные с получением информации от ЛПР. Естественной реакцией на это было стремление получить такую информацию сразу и быстро устранить многокритериальность. Этот подход был реализован путем объединения многих критериев в один с помощью так называемых весовых коэффициентов важности критериев. Глобальный критерий вычисляется по формуле

где C_i – частные критерии; w_i – веса (коэффициенты важности критериев:

0<=w_i <=1; (2)

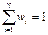Идея такого объединения состоит в том, что ЛПР назначает числа (часто по численной шкале 1-100), представляющие для него ценность рассматриваемого критерия. Считается, что ЛПР может назначить такие числа. Далее весовые коэффициенты нормируются на основе условия (2).

Обратимся к рис., на котором показано множество Эджворта – Парето для двух критериев. Здесь можно увидеть, что решения, соответствующие точкам А и В на множество Парето, могут быть представлены в виде

Существует лемма, утверждающая, что для линейной задачи любое эффективное, находящиеся на множестве Э-П решение может быть представлено в виде (1), т.е. в виде весов, умноженных на частные критерии. Следовательно, формально задача сводится к нахождению весов.