Критерий Смирнова

В критерии Смирнова используют статистику

(10) или статистику , (11) значения которых вычисляют по эквивалентным соотношениям (8), (9).

Реально в критерии обычно используют статистику [3]

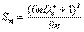, (12)которая при простой гипотезе в пределе подчиняется распределению c² с чис­лом степеней свободы, равным 2.

Гипотезу H₀ не отвергают, если для вычисленного по выборке значения статистики S_m^*

Б6 В1 ДАТЧИКИ ПСЕВДОСЛУЧ ЧИСЕЛ (РЯДОМ))

Появление в настоящее время высокопроизводительных компьютеров существенно расширило область применения метода Монте-Карло для решения самых разнообразных прикладных задач. В основе этого метода лежит использование датчика псевдослучайных чисел при моделировании случайных величин или процессов. В связи с этим весьма актуальной является задача построения качественных датчиков псевдослучайных чисел с заданным распределением. Данная работа посвящена новому методу построения датчика стандартного нормального распределения.

Постановка задачи состоит в следующем. Требуется построить такой алгоритм, который на выходе выдает последовательность случайных чисел, которые независимы и распределены по нормальному закону с нулевым математическим ожиданием и единичной дисперсией.

Существует несколько способов генерирования нормального распределения. Кратко перечислим их:

1. обращение функции распределения;

2. генерирование полярных координат двумерного нормального распределения;

3. использование суммы большого числа независимых равномерно распределенных случайных величин (такая сумма согласно центральной предельной теореме приближенно нормальна).

У каждого из перечисленных методов получения нормального распределения имеются свои достоинства и недостатки, которые в той или иной степени описаны в литературе, и на этом мы здесь останавливаться не будем. Все указанные методы характерны тем, что при генерировании каждого случайного числа требуется по крайней мере одно значение датчика случайных чисел с равномерным на [0,1] распределением. Предлагаемый же в данной работе подход к решению поставленной задачи таков, что для вычисления даже весьма большого количества случайных чисел необходимо воспользоваться лишь относительно малым числом равномерно распределенных случайных чисел.

Основная идея нового метода состоит в следующем. Пусть случайные величины независимы и равномерно распределены на [0,1]. Введем в рассмотрение последовательность комплексных случайных величин вида:

где i - мнимая единица. Cлучайные величины z_k обладают следующими важными свойствами, на которых и базируется новый метод генерирования нормального распределения:

1.

Cлучайные величины некоррелированы.

2.

При в силу центральной предельной теоремы случайные величины z_k асимптотически нормальны и независимы.

3.

Математическое ожидание z_k равняется нулю, а ковариационная матрица равна единичной.

Поэтому, если задать не слишком малое n (например, ) и сгенерировать случайные числа то, вычисляя z_k в соответствии с (1), получаем сколь угодно большую по объему выборку случайных чисел x_k,y_k, которые имеют приближенно стандартное нормальное распределение и независимы. Конечное множество равномерно распределенных случайных чисел порождает в данном методе бесконечную последовательность приблизительно нормальных и независимых случайных чисел. Однако данное утверждение выполняется лишь в том случае, когда числа X_j содержат бесконечное число значащих случайных цифр. На практике все X_j имеют ограниченное число значащих цифр. Рассмотрим более подробно задачу для этого случая.

Пусть теперь случайные величины 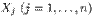независимы и имеют дискретное равномерное распределение на множестве чисел где - число значащих случайных цифр в величинах X_j. Нетрудно показать, что для всех натуральных k, принадлежащих множеству случайные величины z_k, вычисляемые по формуле (1), обладают свойствами 1-3, и, следовательно, эти величины можно использовать для приближенного вычисления 2(10^p-1) стандартных нормальных случайных величин, не зависящих друг от друга. Если же k=m, то z_k принимет значение единица. Кроме того, при дальнейшем увеличении k величины z_k начинают повторятся, т.е. Справедливо также более общее утверждение, состоящее в том, что последовательность является периодической с периодом m=10^p. Увеличивая p, можно получить достаточно большой период этой последовательности. Для формирования случайных цифр чисел X_j желательно использовать некоторые датчики случайных чисел, о хороших свойствах которых заранее известно, например, последовательность цифр числа .

Остановимся далее на чисто технической реализации предложенного метода и оценим необходимые вычислительные затраты. Покажем, что каждое значение может быть получено из предыдущего при помощи только операций умножения и сложения. Действительно, пусть

тогда z_k представляем в следующем виде:

Таким образом, для получения каждого нового значения z_k, необходимо хранить в памяти компьютера 2n комплексных чисел 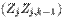и выполнять в соответствии с (2) n операций умножения и n-1 операцию сложения комплексных чисел.

Вычислительная трудоемкость предлагаемого здесь метода несколько выше, чем у многих известных процедур генерирования нормального распределения. Однако он, как уже отмечалось, для каждого нового генерируемого числа, в отличие от других методов, не требует новых значений датчика случайных чисел. Добавим также, что вычисления по формуле (2) легко распараллеливаются, и на компьютерах с соответствующей архитектурой может быть достигнуто значительное уменьшение машинного времени.