Критерий Колмогорова

В случае простых гипотез предельные распределения статистик рассмат­риваемых критериев согласия Колмогорова, Смирнова, w² и W² Мизеса из­вестны и независимы от вида наблюдаемого закона распределения и, в частно­сти, от его параметров. Считают, что эти критерии являются “свободными от распределения”. Это достоинство предопределяет широкое использование дан­ных критериев в различных приложениях.

Предельное распределение статистики

(4)где F_n(x) – эмпирическая функция распределения, F(x,q) – теоретическая функция распределения, n– объем выборки, было получено Колмогоровым в [2]. При n®¥ функция распределения статистики 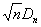сходится равно­мерно к функции распределения Колмогорова

.

(5) Наиболее часто в критерии Колмогорова (Колмогорова-Смирнова) ис­пользуют статистику вида [3]

, (6)

где

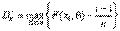, (7) (8) , , (9)

n - объем выборки, x₁,x₂,…,x_n - упорядоченные по возрастанию выборочные значения, F(x) - функция закона распределения, согласие с которым прове­ряют. Распределение величины S_k при простой гипотезе в пределе подчиня­ется закону Колмогорова с функцией распределения K(S).

Если для вычисленного по выборке значения статистики S_k^* выполняется неравенство

P{S> S_k^*}=1-K(S_k^*)>a,

то нет оснований для отклонения гипотезы H₀.