
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ОСНОВНЫЕ ПОНЯТИЯ ФАКТОРНОГО АНАЛИЗА
Под названием модели с латентными переменными будем понимать совокупность статистических моделей, описывающих и объясняющих наблюдаемые данные их зависимостью от ненаблюдаемых характеристик, которые могут быть сконструированы с помощью определенных математических методов [10]. Модель факторного анализа является примером такой модели, в которой общие факторы являются латентными переменными.
Модели с латентными переменными применяются при решении следующих задач:
a. понижение размерности признакового пространства в данных типа “объект-признак",
b. классификация объектов на основе сжатого признакового пространства,
c. косвенные оценки признаков, не поддающихся непосредственному измерению,
d. преобразование исходных переменных к более удобному для интерпретации виду,
e. создание структурной теории исследования объектов.
В большинстве приложений ФА речь идет о выявлении в наблюдаемых признаках  некоторой латентной (скрытой) переменной f, называемой фактором. Гипотеза о наличии этого фактора основано на предположении о существовании чего-то общего в наблюдаемых признаках. В случае существования только одного фактора суть ФА состоит в объяснении корреляции между наблюдаемыми признаками с помощью корреляции этих признаков с фактором
некоторой латентной (скрытой) переменной f, называемой фактором. Гипотеза о наличии этого фактора основано на предположении о существовании чего-то общего в наблюдаемых признаках. В случае существования только одного фактора суть ФА состоит в объяснении корреляции между наблюдаемыми признаками с помощью корреляции этих признаков с фактором 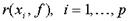 . В общем случае может быть несколько факторов
. В общем случае может быть несколько факторов  . Корреляция между наблюдаемыми признаками и факторами обозначают
. Корреляция между наблюдаемыми признаками и факторами обозначают  . Величины
. Величины  называются факторными нагрузками и они образуют матрицу факторных нагрузок
называются факторными нагрузками и они образуют матрицу факторных нагрузок 
 .
.
Во многих приложениях ФА основная цель состоит в объяснении корреляционной матрицы признаков R ее матрицей факторных нагрузок A. Матрицу Aнаходят численными методами, как правило, определяя собственные числа и векторы матрицы Rприусловии выполнения  .
.
Пример. Рассмотрим основные понятия на простом примере.Пусть дана матрица “объект -признак”, описывающая данные измерений n объектов из четырех переменных 
 .Вычисленная корреляционная матрица матрицы наблюдений Xравна
.Вычисленная корреляционная матрица матрицы наблюдений Xравна  . (7.1)
. (7.1)
Наблюдается тесная связь между переменными  и
и  с коэффициентом корреляции
с коэффициентом корреляции  = 0.72, переменная
= 0.72, переменная  связана слабее с первыми двумя, а
связана слабее с первыми двумя, а 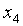 - не зависит от всех остальных переменных.
- не зависит от всех остальных переменных.
Целью факторного анализа является нахождение латентной переменной, так называемого фактора, который бы позволил воспроизвести наблюдаемую корреляционную матрицу с использованием соответствующей процедуры вычислений. Редуцированную (преобразованную) корреляционную матрицу  можно воспроизвести с помощью вектора
можно воспроизвести с помощью вектора  факторной нагрузки по уравнению
факторной нагрузки по уравнению 
 . (7.2)
. (7.2) 

 Вектор
Вектор  =[0.90 0.80 0.50 0.05] представляет собой факторную нагрузку ненаблюдаемого фактора. В результате умножения
=[0.90 0.80 0.50 0.05] представляет собой факторную нагрузку ненаблюдаемого фактора. В результате умножения  получим матрицу
получим матрицу  , отличающуюся от
, отличающуюся от  диагональными элементами. Диагональные элементы матрицы
диагональными элементами. Диагональные элементы матрицы  (элементы в скобках) называются общностями. Общность i - того элемента будем обозначать через
(элементы в скобках) называются общностями. Общность i - того элемента будем обозначать через  . Величина
. Величина  называется характерностью. Диагональные элементы исходной и редуцированной корреляционных матриц связаны соотношением
называется характерностью. Диагональные элементы исходной и редуцированной корреляционных матриц связаны соотношением
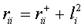 . (7.3) Таким образом значения компонент вектора
. (7.3) Таким образом значения компонент вектора  , называемых факторными нагрузками, воспроизводят все коэффициенты корреляции для четырех переменных. Фактор
, называемых факторными нагрузками, воспроизводят все коэффициенты корреляции для четырех переменных. Фактор  непосредственно для измерения недоступен - он гипотетичен. Факторный анализ призван для установления таких гипотетичных факторов. Из приведенного примера ясно, что прежде чем определить фактор нужно построить редуцированную корреляционную матрицу
непосредственно для измерения недоступен - он гипотетичен. Факторный анализ призван для установления таких гипотетичных факторов. Из приведенного примера ясно, что прежде чем определить фактор нужно построить редуцированную корреляционную матрицу  по значениям общностей. Оценка общностей составляют первую проблему факторного анализа, проблему общности. Второй проблемой является определение фактора. Это так называемая проблема факторов.
по значениям общностей. Оценка общностей составляют первую проблему факторного анализа, проблему общности. Второй проблемой является определение фактора. Это так называемая проблема факторов.
В общем случае для объяснения корреляционной матрицы потребуется не один, а несколько факторов. Каждый фактор характеризуется столбцом,каждая переменная - строкойматрицы А. Фактор называется генеральным(general factor),если все его нагрузки значительно отличаются от нуля и он имеет нагрузки от всех переменных. Генеральный фактор имеет нагрузки от всех переменных и схематически такой фактор изображен на рис.7.1 столбцом  .Фактор называется общим (common factor), если хотя бы две его нагрузки значительно отличаются от нуля. Столбцы
.Фактор называется общим (common factor), если хотя бы две его нагрузки значительно отличаются от нуля. Столбцы 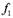 ,
,  ,
,  на рис.7.1 представляют такие общие факторы. Они имеют нагрузки от более чем двух переменных. Если у фактора только одна нагрузка, значительно отличающаяся от нуля, то он называется характерным фактором (unique factor) (см. столбцы
на рис.7.1 представляют такие общие факторы. Они имеют нагрузки от более чем двух переменных. Если у фактора только одна нагрузка, значительно отличающаяся от нуля, то он называется характерным фактором (unique factor) (см. столбцы  на рис. 7.1.
на рис. 7.1.

Рис. 7.1. Схематическое изображение факторного отображения.
Крестик  означает высокую факторную нагрузку.
означает высокую факторную нагрузку.
Каждый такой фактор представляет только одну переменную. Решающее значение в факторном анализе имеют общие факторы. Если общие факторы установлены, то характерные факторы получаются автоматически. Число высоких нагрузок переменной на общие факторы называется сложностью (complexity). Например, переменная  на рис.7.1 имеет сложность 2, а переменная
на рис.7.1 имеет сложность 2, а переменная  - три.
- три.
Итак мы пытаемся построить модель
 ,
, 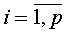 , (7.4)
, (7.4)
где  - ненаблюдаемые факторы k < p,
- ненаблюдаемые факторы k < p, 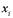 - наблюдаемые переменные (исходные признаки),
- наблюдаемые переменные (исходные признаки),
 ,
,  - факторные нагрузки,
- факторные нагрузки, 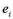 - случайная ошибка связанная только с
- случайная ошибка связанная только с  с нулевым средним и дисперсией
с нулевым средним и дисперсией 
 ,
,  ,
,  и
и  - некорpелированы
- некорpелированы  ,
,
 - некоррелированные случайные величины с нулевым средним и единичной дисперсией
- некоррелированные случайные величины с нулевым средним и единичной дисперсией  .
.
Тогда
 . (7.5) Здесь
. (7.5) Здесь  - i-ая общность представляющая собой часть дисперсии
- i-ая общность представляющая собой часть дисперсии 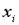 , обусловленная факторами,
, обусловленная факторами,
 - часть дисперсии
- часть дисперсии  , обусловленная ошибкой.
, обусловленная ошибкой.
В матричной записи факторная модель (7.4) примет вид
X = AF + e, (7.6)
где  матрица нагрузок, F- k - вектор факторов, e - вектор ошибок.
матрица нагрузок, F- k - вектор факторов, e - вектор ошибок.  , (7.7)
, (7.7)
где  -диагональная матрица порядка p, содержащая дисперсии ошибок.
-диагональная матрица порядка p, содержащая дисперсии ошибок.
Дата добавления: 2015-01-19; просмотров: 346; Мы поможем в написании вашей работы!; Нарушение авторских прав |