
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
НЕКОТОРЫЕ СВОЙСТВА
1. Факторный анализ, как и главные компоненты позволяет, сократить размерность признакового пространства. Оба метода являются эффективными способами исследовании взаимосвязей между переменными. Основное различие между этими методами заключается в том, что главные компоненты являются линейными функциями от наблюдаемых переменных, в то время как общие факторы не выражаются через комбинацию исходных признаков. Главные компоненты не объясняют корреляции между переменными. В случае некоррелированных данных главных компонент не существует. Факторный анализ представляет корреляционную структуру в терминах гипотетической (латентной) модели, в то время как анализ главных компонент сокращает размерность за счет использования нескольких линейных комбинаций исходных переменных. Таким образом факторный анализ ориентирован на задачи, несколько отличные от задач главных компонент.
2. В отличии от главных компонент факторный анализ (разложение матрицы Kx) нечувствителен к изменению шкал. Действительно, если умножаем каждую переменную xi на  , то условия на
, то условия на  дисперсия не изменяется , наши факторные нагрузки будут иметь вид
дисперсия не изменяется , наши факторные нагрузки будут иметь вид
 ,
,  и вместо Kx будем иметь Rx, и
и вместо Kx будем иметь Rx, и  , (7.8)
, (7.8)  . (7.9)
. (7.9)
3. Факторное решение не единственно. Если В -ортогональная матрица (k  k), то
k), то
X=AF+L
и разложение Х можно переписать
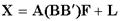 .
.
Но  =I , поэтому заА взять АВ, а за F -
=I , поэтому заА взять АВ, а за F -  и разложение Kx, примет прежний вид
и разложение Kx, примет прежний вид  (7.10)
(7.10)
Последнее означает что имеется бесконечное число факторных нагрузок , удовлетворяющих исходным предпосылкам, структур (A,L2). Эту трудность можно преодолеть, если ввести на А ограничение.
Рассмотрим матричное уравнение (7.10) подробнее. В левой части уравнения с учетом симметрии 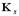 число коэффициентов равно р(р+1)/2. В правой части р(k+1).
число коэффициентов равно р(р+1)/2. В правой части р(k+1).
Если k+1>(р+1)/2, то однозначное решение факторной задачи невозможно. Будем нормализовать постоянные А,полагая 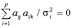 ,
, 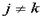 ,
,
что эквивалентно ,что
 , (7.11) где J -диагональная (
, (7.11) где J -диагональная ( 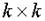 ) матрица ,что накладывает еще
) матрица ,что накладывает еще  ограничений .
ограничений .
В результате имеем
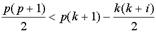 или
или 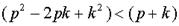 (7.12) Если
(7.12) Если  , (7.13)
, (7.13)
то система уравнений остается неопределенной
Андерсен вывел другое соотношение единственности решения: при вычеркивании из А любой строки, оставшуюся часть матрицы можно было бы разделить на две подматрицы ранга k
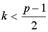 . (7.14)
. (7.14)
Это условие дает такие же результаты, что и предыдущее уравнение. Отсюда случаи:
p = 2 и k = 1;
p = 4 и k = 2
не допускают идентификации. Число независимых коэффициентов 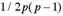 при заданном числе переменных p имаксимальном числе факторов k для положительного числа степеней свободы Максимально возможное число факторов, которое удается извлечь из данной корреляционной матрицы порядка p равно
при заданном числе переменных p имаксимальном числе факторов k для положительного числа степеней свободы Максимально возможное число факторов, которое удается извлечь из данной корреляционной матрицы порядка p равно 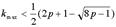 .
.
Дата добавления: 2015-01-19; просмотров: 223; Мы поможем в написании вашей работы!; Нарушение авторских прав |