Б13 В3 Операции над нечеткими множеств

Определения нечетких теоретико-множественных операций объединения, пересечения и дополнения могут быть обобщены из обычной теории множеств. В отличие от обычных множеств, в теории нечетких множеств степень принадлежности не ограничена лишь бинарной значениями 0 и 1 ‑ она может принимать значения из интервала [0, 1]. Поэтому, нечеткие теоретико-множественные операции могут быть определены по-разному. Ясно, что выполнение нечетких операций объединения, пересечения и дополнения над не нечеткими множествами должно дать такие же результаты, как и при использование обычных канторовских теоретико-множественных операций. Ниже приведены определения нечетких теоретико-множественных операций, предложенных Л. Заде.

Определение 20. Дополнением нечеткого множества заданного на называется нечеткое множество с функцией принадлежности для всех . На рис. 4 приведен пример выполнения операции нечеткого дополнения.

Рисунок 4 - Дополнение нечеткого множества

Определение 21. Пересечением нечетких множеств и заданных на называется нечеткое множество с функцией принадлежности для всех . Операция нахождения минимума также обозначается знаком , т.е. .

Определение 22. Объединением нечетких множеств и заданных на называется нечеткое множество с функцией принадлежности для всех . Операция нахождения максимума также обозначается знаком , т.е. .

Обобщенные определения операций нечеткого объединения и пересечения - треугольной нормы (t-нормы) и треугольной конормы (t-конормы или s-нормы) приведены ниже.

Определение 23. Треугольной нормой (t-нормой) называется бинарная операция 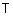на единичном интервале , удовлетворяющая следующим аксиомам для любых :

1. (граничное условие);

2. если (монотонность);

3. (коммутативность);

4. (ассоциативность).

Наиболее часто используются такие t-нормы: пересечение по Заде ‑ ; вероятностное пересечение ‑ ; пересечение по Лукасевичу ‑ . Примеры выполнения пересечения нечетких множеств с использованием этих t-норм показаны на рис. 5.

Рисунок 5 - Пересечение нечетких множеств с использованием различных t-норм

Определение 25. Треугольной конормой (s-нормой) называется бинарная операция на единичном интервале , удовлетворяющая следующим аксиомам для любых :

1. (граничное условие);

2. если (монотонность);

3. 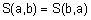(коммутативность);

4. (ассоциативность).

Наиболее часто используются такие s-нормы: объединение по Заде ‑ 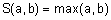; вероятностное объединение ‑ 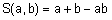; объединение по Лукасевичу ‑ . Примеры выполнения объединения нечетких множеств с использованием этих s-норм показаны на рис. 6.

Наиболее известные треугольные нормы приведены в табл. 1.

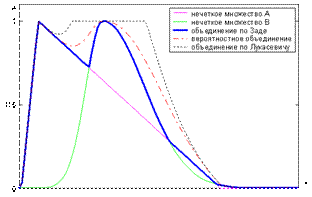
Рисунок 6 - Объединение нечетких множеств с использованием различных s-норм

Таблица 1 - Примеры треугольных норм

		Параметр
		‑
		‑
		‑
		‑

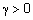
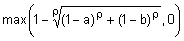
Б14 В3 Нечеткая арифметика ???????????????

В этом разделе рассматриваются способы расчета значений четких алгебраических функций от нечетких аргументов. Материал основывается на понятиях нечеткого числа и принципа нечеткого обобщения. В конце раздела приводятся правила выполнения арифметических операций над нечеткими числами.

Определение 25. Нечетким числом называется выпуклое нормальное нечеткое множество с кусочно-непрерывной функцией принадлежности, заданное на множестве действительных чисел. Например, нечеткое число "около 10" можно задать следующей функцией принадлежности: .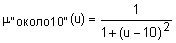

Определение 26. Нечеткое число называется положительным (отрицательным) если , ( ).

Определение 27. Принцип обобщения Заде. Если ‑ функция от n независимых переменных и аргументы заданы нечеткими числами , соответственно, то значением функции называется нечеткое число с функцией принадлежности:

.

Принцип обобщения позволяет найти функцию принадлежности нечеткого числа, соответствующего значения четкой функции от нечетких аргументов. Компьютерно-ориентированная реализация принципа нечеткого обобщения осуществляется по следующему алгоритму:

Шаг 1. Зафиксировать значение .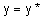

Шаг 2. Найти все n-ки , , 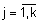удовлетворяющие условиям и , .

Шаг 3. Степень принадлежности элемента нечеткому числу вычислить по формуле: .

Шаг 4. Проверить условие "Взяты все элементы y?". Если "да", то перейти к шагу 5. Иначе зафиксировать новое значение и перейти к шагу 2.

Шаг 5. Конец.

Приведенный алгоритм основан на представлении нечеткого числа на дискретном универсальном множестве, т.е. 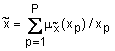. Обычно исходные данные , задаются кусочно-непрерывными функциями принадлежности: . Для вычисления значений функции аргументы , дискретизируют, т.е. представляют в виде . Число точек 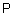выбирают так, чтобы обеспечить требуемую точность вычислений. На выходе этого алгоритма получается нечеткое множество, также заданное на дискретном универсальном множестве. Результирующую кусочно-непрерывную функцию принадлежности нечеткого числа получают как верхнюю огибающую точек .

Пример 4.Нечеткие числа и заданы следующими трапециевидными функциями принадлежности:

и .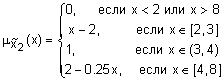

Необходимо найти нечеткое число 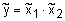с использованием принципа обобщения из определения 27.

Зададим нечеткие аргументы на четырех точках (дискретах): {1, 2, 3 4} для и {2, 3, 4 8} для . Тогда: и . Процесс выполнения умножения над нечеткими числами сведен в табл. 2. Каждый столбец таблицы соответствует одной итерации алгоритма нечеткого обобщения. Результирующее нечеткое множество задано первой и последней строчками таблицы. В первой строке записаны элементы универсального множества, а в последней строке - степени их принадлежности к значению выражения . В результате получаем: . Предположим, что тип функция принадлежности будет таким же, как и аргументов и , т. е. трапециевидной. В этом случае функция принадлежности задается выражением: . На рис. 7 показаны результаты выполнения операции 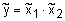с представлением нечетких множителей на 4-х дискретах. Красными звездочками показаны элементы нечеткого множества из табл. 2, а тонкой красной линией - трапециевидная функция принадлежности.

Исследуем, как измениться результат нечеткого обобщения при увеличении числа дискрет, на которых задаются аргументы. Нечеткое число при задании аргументов и на 30 дискретах приведено на рис. 7. Синими точками показаны элементы нечеткого множества , найденные по принципу обобщения, а зеленой линией - верхняя огибающая этих точек ‑ функция принадлежности . Функция принадлежности результата имеет форму криволинейной трапеции, немного выгнутой влево.

Таблица 2 - К примеру 4

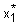
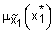
Рисунок 7 - К примеру 4

Применение принципа обобщения Заде сопряжено с двумя трудностями:

1. большой объем вычислений - количество элементов результирующего нечеткого множества, которые необходио обработать, равно 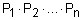, где ‑ количество точек, на которых задан i-й нечеткий аргумент, ;

2. необходимость построения верхней огибающей элементов результирующего нечеткого множества.

Более практичным является применение -уровневого принципа обобщения. В этом случае нечеткие числа представляются в виде разложений по -уровневым множествам: , где ‑ минимальное (максимальное) значение на -уровне.

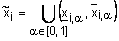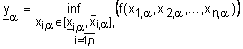Определение 28. -уровневый принцип обобщения. Если ‑ функция от n независимых переменных и аргументы заданы нечеткими числами , , то значением функции называется нечеткое число , где и .

Применение -уровневого принципа обобщения сводится к решению для каждого -уровня следующей задачи оптимизации: найти максимальное и минимальное значения функции при условии, что аргументы могут принимать значения из соответствующих -уровневых множеств. Количество -уровней выбирают так, чтобы обеспечить необходимую точность вычислений.

Пример 5. Решить задачу из примера 4 применяя -уровневый принцип обобщения.

Будем использовать 2 следующих -уровня:{0, 1}. Тогда нечеткие аргументы задаються так: и . По -уровневому принципу обобщения получаем: . На рис. 8 показан результат умножения двух нечетких чисел 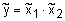: красными горизонтальными линиями изображены -сечения, а тонкой красной линией - кусочно-линейная аппроксимация функции принадлежности нечеткого числа .

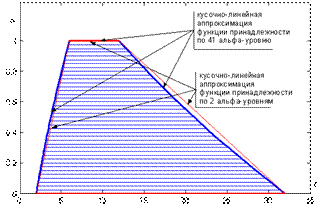Исследуем, как измениться результат нечеткого обобщения при увеличении числа -уровней. Нечеткое число при задании аргументов и на 41 -уровне показано на рис. 8. Синими горизонтальными линиями изображены -сечения нечеткого множества, а жирной синей линией -кусочно-линейная аппроксимация функции принадлежности нечеткого числа для 41 -уровня. Сравнивая рис. 7 и 8, видим, что результаты обобщения по определениям 27 и 28 близки.

Рисунок 8 - К примеру 5

Применение -уровневого принципа обобщения позволяет получить правила выполнения арифметических операций над нечеткими числами. Правила выполнения арифметических операций для положительных нечетких чисел приведены в табл. 3. Эти правила необходимо применять для каждого -уровня.

Таблица 3 -Правила выполнения арифметических операций для положительных нечетких чисел (для каждого -уровня)

Арифметическая операция

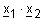
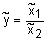
Б15 В2 Оценка методов и систем имитационного моделирования (МОЖНО И РАССКАЗАТЬ В Б23 В1)

Наиболее широкое применение методика имитационного моделирования находит при исследовании систем массового обслуживания (СМО). В настоящее время для имитационного моделирования разработано большое количество специальных языков (GPSS, SLAM, GASP, SIMSCRIPT и др.). Не будем останавливаться на особенностях имитационного моделирования с помощью этих языков – достаточно хороший анализ этих и других языков имитационного моделирования приведен в работах [1, 4–8]. Эти языки (и их модификации), как правило, написаны или базируются на других языках типа: ассемблер, фортран, паскаль или других языках высокого уровня. При этом авторы разработок этих языков в качестве основных положительных качеств своих разработок зачастую отмечают простоту и компактность разрабатываемых моделей и отсутствие необходимости в изучении достаточно сложных языков программирования, которые послужили базовой основой для этих разработок. Конечно это не совсем так: чтобы грамотно и достаточно адекватно описать моделируемую систему необходимо знать все тонкости не только языка моделирования, на котором разрабатывается имитационная модель, но и среду моделирования и базовый язык программирования.

Рассмотрим особенности имитационного моделирования систем массового обслуживания тремя методами: 1) с применением только языков высокого уровня (далее для простоты этот метод будем называть ЯВУ); 2) с применением языка моделирования SIMPAS [5], событийная часть которого основана на языке моделирования GPSS [8]; 3) с применением языка (и пакета) визуально-ориентированного программирования SIMULINK, входящего составной частью в систему MATLAB [2, 3].

Приведем характеристику методов и систем имитационного моделирования, рассмотренных выше.

1. Метод ЯВУ (языки программирования Pascal, С, С++ и их модификации):

а) в изучении эти языки достаточно сложны, причем этим отличается в большей степени язык С++; б) язык Pascal по сравнению с языками типа С, С++ отличается простотой программирования, хотя версия этого языка с указателями, объектами и т. п. по сложности программирования приближается к языку С++, а система DELPHI по своим возможностям близка к системе Borland C++ Builder; в) по сравнению с системами моделирования SIMPAS и SIMULINK метод ЯВУ отличается хорошей гибкостью в использовании различных подходов моделирования.

2. Система имитационного моделирования SIMPAS: а) сравнительно проста в изучении; б) однако при программировании требуется знать кроме самой системы моделирования SIMPAS также и систему программирования Pascal; в) очевидно, что выигрывая в простоте изучения и программировании, эта система проигрывает в гибкости использования различных подходов моделирования.

3. Система визуально-ориентированного программирования SIMULINK, примененная для имитационного моделирования: а) отличается сравнительной сложностью (по сравнению с системой имитационного моделирования SIMPAS) при изучении и простотой при программировании; б) по удобству графического пользовательского интерфейса, по обилию компонентов в множестве библиотек, разнообразию виртуальных средств регистрации и визуализации результатов моделирования эта система выгодно отличается от других систем моделирования.