Б18 В1 МЕТОДОЛОГИЯ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ РАСПРЕДЕЛЕННЫХ ИНТЕЛЛЕКТУАЛЬНЫХ ИНФОРМАЦИОННЫХ СИСТЕМ

С. А. Яковлев (Санкт-Петербург)

Имитационное моделирование (ИМ) является эффективным инструментом оценки характеристик процессов функционирования сложных систем на этапах их исследования и проектирования. Но этим возможности данного метода не ограничиваются: в современных системах управления ИМ используется непосредственно в контуре управления, на его основе решаются задачи прогнозирования для принятия решений по управлению территориально разнесенным объектом, т. е. реализуются распределенные интеллектуальные информационные системы (РИИС). Построение РИИС стало возможным, с одной стороны, после решения вопросов информационного подхода к проблеме управления, а с другой стороны, после проработки задач ИМ в реальном масштабе времени (РМВ) на современных ЭВМ с учетом ограниченности ресурсов.

Одной из центральных проблем современной теории управления является проблема интеллектуализации управления динамическими объектами в условиях неопределенности, т. е. проблема построения адаптивных систем, принцип работы которых основан на изменении параметров и структуры в результате наблюдения и обработки текущей информации так, чтобы адаптивная или обучающая система с течением времени улучшила свое функционирование, достигая в конечном итоге оптимального состояния. В адаптивных системах недостаток априорной информации компенсируется благодаря целенаправленной обработке текущей информации. Рассмотрим возможность и особенности использования имитационных моделей М_и для решения основных задач построения РИИС.

Под адаптацией понимается процесс изменения структуры, алгоритмов и параметров системы Sна основе информации, получаемой в процессе управления с целью достижения оптимального (в смысле принятого критерия) состояния или поведения системы при начальной неопределенности и изменяющихся условиях работы системы во взаимодействии с внешней средой Е. Адаптация использует обучение и самообучение для получения в условиях неопределенности информации о состояниях и характеристиках объекта, необходимой для оптимального управления. Обучение понимается как процесс выработки в некотором объекте тех или иных свойств его реакции на внешние воздействия путем многократных испытаний и корректировок. Самообучение отлича­ется от обучения отсутствием внешней корректировки.

Характерная черта адаптации – текущее накопление информации о процессе функционирования системы S и внешней среды E и ее использование для улучшения избранного показателя качества. Процесс накопления информации связан с затратами времени, что в итоге приводит к запаздыванию в получении системой управления информации, необходимой для принятия решений. Это существенно снижает эффективность работы систем управления в реальном масштабе времени. Поэтому актуальной является задача прогнозирования состояний (ситуаций) системы Sи внешней среды Еи характеристик (поведения) системы Sдля адаптивного управления. Такой прогноз может быть выполнен при использовании методов ИМ в системе управления в РМВ.

Создание и развитие теории ИМ обусловлено, прежде всего, неполнотой априорной информации о процессе функционирования исследуемого объекта (в нашем случае РИИС и ее элементов). Именно от объема априорной информации зависит и математическая постановка задачи, а часто этим определяется не только подход, но и метод ее решения. Исходя из того, что элементы РИИС часто являются мало изученными объектами, т. е. практически отсутствуют априорные сведения о них, напрашивается вывод о необходимости построения непараметрических систем адаптации. Но для такой сложной системы, как РИИС, следует отметить возникающие существенные трудности при использовании непараметрической адаптации для всей системы, т. е. при практическом рассмотрении объекта управления как «черногоящика»: сложность методов и громоздкость алгоритмов адаптивного управления и, как следствие, их практическая нереализуемость с учетом ограничений вычислительных ресурсов РИИС, а часто и необходимости управления в РМВ.

Создание РИИС требует наличия большого объема информации, как о самом объекте, так и о его входных и выходных переменных. Эта информация необходима для построения адекватной модели РИИС, на основе которой может быть эффективно осуществлен процесс управления. При этом следует различать два вида информации, необходимой для построения и совершенствования модели: априорную и текущую. Априорная информация об объекте, его входных и выходных переменных, внутренних состояниях необходима для построения ИМ, по которой будет создаваться РИИС: выбираться структура, алгоритмы и параметры системы, критерий функционирования. Обычно для сложных вновь проектируемых РИИС задача должна решаться в условиях недостаточной или вовсе отсутствующей априорной информации об объекте. Речь идет об отсутствии информационной («управленческой») модели объекта, устанавливающей взаимосвязь между выходными и входными переменными.

Проблема создания РИИС неизбежно возникает при разработке систем и при их модернизации. На первый взгляд может показаться, что в тех случаях, когда новая
РИИС разрабатывается для системы S, длительное время находящейся в эксплуатации, положение с априорной информацией лучше и построение модели проще. Опыт показывает, что это не так, и получение информационной модели и в этом случае весьма трудоемко. Таким образом, как для случая вновь проектируемой системы S, так и для уже функционирующей возникает проблема получения дополнительной информации для создания РИИС. Единственным эффективным путем получения такой информации в настоящее время является ИМ. В том случае, когда РИИС создана и функционирует, существует необходимость в получении текущей информации, вызванная в основном двумя причинами. Во-первых, это потребность в совершенствовании РИИС, а во-вторых, необходимость уточнения поведения системы и возникающих в ней ситуаций с целью компенсации изменений характеристик системы S. Процессы, с которыми связана текущая информация первого вида, являются достаточно медленными и для управления ими необходима подсистема эволюционного управления, а процессы второго типа являются более быстрыми и для управления ими необходима подсистема оперативного управления в реальном масштабе времени (РМВ).

Следует подчеркнуть, что по темпу принятия решений и месту решения задач подсистемы эволюционного и оперативного управления существенно отличаются друг от друга. Так, например, процессы оперативного управления могут быть на несколько порядков более быстрыми по сравнению с процессами эволюционного управления. Важнейшей задачей современной теории и практики является построение модели, т. е. формализация закономерностей функционирования объекта. На основе этой модели определяются структура, алгоритмы и параметры РИИС, выбираются аппаратно-программные средства реализации системы. Одним из эффективных методов построения модели сложного объекта является идентификация.

Широкое развитие в настоящее время работ по формализации процессов и построению их моделей во многих областях исследований (технике, экономике, социологии и т. д.) преследуют две основные цели. Первая из них связана со значительным увеличением возможностей изучения на базе ЭВМ сложных процессов функционирования различных объектов при помощи метода моделирования, для чего необходимо математическое описание исследуемого процесса. Не меньшее значение в технических системах имеют модели, используемые для достижения второй цели, т. е. применяемые непосредственно в контуре управления объектами.

Невозможность ограничиться только одной универсальной моделью связана с тем, что, с одной стороны, перед этими моделями ставятся различные цели, а с другой стороны, они описывают процессы, протекающие в различных масштабах времени, причем степень полноты модели, ее соответствие реальному объекту зависят от целей, для которых эта модель используется. Модели первого типа имеют в основном гносеологический характер, от них требуется тесная связь с методами той конкретной области знаний, для которой они строятся. Модели такого типа являются достаточно «инерционными» в своем развитии, так как отражают эволюцию в конкретной области зна­ний. Такие модели будем называть эволюционными. Модели второго типа имеют информационный характер и должны соответствовать конкретным целям по принятию решений по управлению объектом, который они описывают. Такие модели будем называть десиженсными. Деление на гносеологические (эволюционные) и информационные (десиженсные) модели достаточно условно, но оно удобно для отражения целей моделирования.

В информационных моделях, используемых непосредственно для принятия решений в РИИС, требование оперативности является одним из основных. Оно вызвано тем, что при каждом воздействии на объект необходимо в модели учесть действительные изменения, происшедшие в объекте, и внешние возмущения, на основе которых рассчитывается управление. Это требование оперативности, т. е. необходимость работы такой модели в РМВ, часто ведет к отказу от сложных и точных моделей, к разработке специальных, так называемых робастных, алгоритмов построения моделей, использование которых в РИИС обычно ведет к поставленной цели.

Появление идентификации в начале 60-х годов было связано с острой необходимостью разработки методов построения именно информационных моделей объектов управления. Отсутствие таких моделей сдерживало процесс автоматизации этих объектов, использования ЭВМ в контуре управления. Объекты оказались неподготовленными к внедрению вычислительной техники из-за отсутствия их математического описания, их информационных моделей. Построение информационной модели методами идентификации должно быть направлено на ликвидацию этого разрыва и разработку методов оперативного получения модели объекта. При этом методы идентификации должны предусматривать использование ЭВМ для решения задач построения информационной модели.

Отсутствие формальных методов перехода от гносеологических моделей к информационным в современной теории управления не дает возможности получить по имеющейся информации адекватное описание, необходимое для создания РИИС. Но учет сведений, содержащихся в гносеологических моделях, может значительно увеличить объем априорной информации о рассматриваемой РИИС. Поставив цель построения гносеологической модели процесса функционирования системы Sдля получения необходимой априорной информации для построения эффективной РИИС и сузив класс объектов моделирования до конкретного, т. е. до поведения конкретной системы S, решим задачу построения прикладной теории эволюционного и десиженсного моделирования, позволяющей эффективно (в реализационном аспекте) перейти от гносеологических («исследовательских») моделей к информационным («управленческим») моделям. Наиболее просто такой переход можно совершить, если оба этих класса моделей будут базироваться на единую концептуальную модель, использовать единую систему информации (базу знаний) и иметь единую критериальную систему.

Вопрос применимости некоторой математической модели к изучению рассматриваемого объекта не является чисто математическим вопросом и не может быть решен математическими методами. Только критерий практики позволяет сравнивать различные гипотетические модели и выбрать из них ту, которая является наиболее простой и в то же время правильно передает свойства изучаемого объекта, т. е. системы S. Ориентируясь на общие вопросы методологии моделирования сложных технических систем, сформулируем требования к прикладной теории моделирования, а точнее – к элементам этой теории в ее приложении для решения конкретно поставленной задачи. Как уже отмечалось выше, эта задача ставится следующим образом. Необходимо сначала построить и реализовать на ЭВМ эволюционную модель процесса функционирования системы S, полученную в ходе стратегической идентификации объекта, а затем на ее базе построить десиженсную модель, используемую для решения практических задач оперативного управления в РИИС. Или, используя терминологию теории идентификации, необходимо построить конкретную дискретную адаптивную систему управления с идентификатором и предсказателем (комбинированную) в цепи обратной связи, т. е. реализовать сначала стратегический идентификатор, а затем на его базе тактический оперативный иден­тификатор и предсказатель, рассматривая в качестве объекта не реальную систему S(ввиду ее отсутствия), а ИМ процесса ее функционирования. Таким образом, можно поставленную задачу трактовать и как задачу

автоматизации исследования объекта (имитационной модели М_и) для целей синтеза тактической и оперативной модели, используемой непосредственно в контуре управления системой S, а затем для проверки эффективности РИИС в целом.

Прежде чем переходить к изложению элементов теории моделирования процессов в системе S, дадим ряд определений. Напомним, что под моделированием будем понимать исследование объекта посредством изучения его модели, т. е. другого объекта, более удобного для этой цели. Под сложностью моделируемого объекта будем понимать фактически сложность сведений о нем (его описания), зависящую от целей моделирования и уровня, на котором выполняется описание. Таким образом, сложность возрастает не только при введении в рассмотрение новых качеств, но и при переходе к более детальному описанию процесса функционирования объекта моделирования, т. е. системы S.

Задачу прикладной теории моделирования сформулируем, исходя из тех требований, которые будет предъявлять к ней пользователь (исследователь, разработчик системы S), проводящий эксперименты с процессами функционирования и ее элементов для решения конкретной прикладной задачи. В таком контексте основной задачей при решении проблем управления является выбор моделей на уровне оперативного управления, сохраняющих при этом существенные для РИИС с учетом ограничений реализации в РМВ (особенно при оперативном управлении). В дальнейшем модель, практически реализуемую с учетом ограниченности ресурсов, будем называть трактабельной. Таким образом, помимо теоретических вопросов построения модели вообще будем рассматривать вопросы трактабельности модели, связанные с формальным представлением ее описания, его упрощением, проверкой адекватности упрощенной модели и т. д.

Тот факт, что моделируемая система Sсуществует лишь как замысел разработчика, вносит в проблему разработки такой теории значительные трудности. В частности, не удается непосредственно проверить адекватность модели процесса функционирования системы S с помощью реального объекта. Частично эта трудность устраняется путем проведения натурных экспериментов с элементами S. Ряд существенных трудностей возникает из-за неполноты исходной информации об объекте моделирования.

Большой объем знаний о системах и их элементах, накопленный к настоящему времени, подлежащий объединению в рамках теории моделирования и несоизмеримый с познавательными возможностями одного исследователя, выдвигает необходимость организации и детализации таких знаний (теории) в систему, затрагивающую лишь существенно ограниченное число объектов при сохранении общности подхода. При этом развитие отдельных методов статистического моделирования, языков моделирования, теории планирования машинных экспериментов и т. д. оказывается недостаточным.

Создание прикладной теории, обеспечивающей конкретные потребности разработчика модели и охватывающей весь процесс моделирования в широком смысле этого слова, требует системного подхода и, прежде всего, установления основ теории: понятий об объекте, предмете, содержании, структуре и логике теории.

Объектом разрабатываемой прикладной теории является непосредственно процесс моделирования поведения системы S, т. е. процесс перехода от моделируемого объекта (системы S) сначала к статической модели S^s, используемой при стратегической идентификации, а затем и к динамической модели D^ss, непосредственно используемой при оперативном управлении с использованием методов и алгоритмов РИИС. При этом ориентируются на критериальную систему K. Такой переход осуществляется через описание (концептуальную модель), фиксирующее сведения об объекте Sв понятиях языка L(терминах типовых математических схем). При выборе математической схемы моделирования Mвводится также понятие среды S, позволяющее использовать информацию прикладного характера J о целях моделирования, законах функционирования системы S, имеющемся математическом аппарате и т. д. для исследования методов и алгоритмов управления системой A.

Таким образом, так как объектом данной прикладной теории моделирования является процесс моделирования, то возникает необходимость в построении и изучении «модели моделей», или репромодели RМ(от англ. reproduce – воспроизводить, порождать). Репромодель представляет собой упрощенный и наглядный прототип создаваемых моделей, используемых в РИИС, и дает возможность эффективного приближения к таким моделям с максимальным использованием априорной и оперативной информации о поведении системы S, поступающей в процессе ее функционирования.

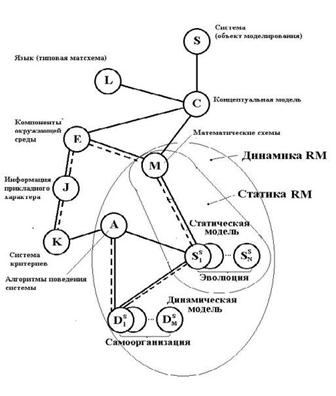
Для решения поставленной задачи разработки модели для РИИС схема репромодели приведена на рисунке. После того как сформулирована концептуальная модель С и введены понятия компонент сред S, основное содержание элементов прикладной теории моделирования для управления системой составят компоненты М, А, S^s и D^s(критерий К считается заданным), причем переход от М к S^s составит статику моделирования, а переход от М к множеству D^s с привлечением информации из компонент S^s и А составит динамику моделирования. Такое разделение на статику и динамику условно показано на рисунке пунктирной и сплошной линиями соответственно.

Движение в пространстве статических моделей процесса функционирования системы S^s назовем эволюцией (или эволюционным моделированием), а движение в пространстве динамических (активных) моделей D , используемых в контуре управления,– самоорганизацией (или моделированием с самоорганизацией). Важно отметить, что компоненты объекта теории L, С, Е, М имеют искусственное происхождение, базирующееся на эвристических представлениях, и могут при необходимости изменяться (развиваться) в интересах самой прикладной теории. Это существенно отличает прикладную теорию моделирования от естественно-научных теорий. (РИС)

Высказывания, составляющие любую теорию, формируются относительно предмета теории, а именно системы понятий, отображающих с той или иной степенью обобщения объект теории (репромодель). Таким образом, задание предмета прикладной теории моделирования процессов в системе S равносильно заданию репромоделей. Очевидно, что вообще различным репромоделям должны соответствовать различные аспекты теории. Применительно к РИИС сужаем круг этих аспектов за счет конкретизации целей моделирования путем введения в репромодель компонент А, ограниченных методами и алгоритмами оперативного управления. Построение репромодели по схеме, приведенной на рисунке, позволяет использовать как информацию общего характера о процессах моделирования и управления J, так и конкретную информацию о методах и алгоритмах управления системой Sс учетом выбранных критериев оценки эффективности К.

Содержание прикладной теории моделирования охватывает две части: базис J теории, включающей систему эвристических принципов, полученных при обобщении имеющегося опыта моделирования сложных объектов вообще, и тело теории, содержащее эвристические правила имитационной реализации конкретных моделей процесса функционирования S (S^s и D^s).

Предложения теории, относящиеся к компонентам М, A, S^s и D^sили возможным переходам между ними, содержат множество условий, позволяющих точно их сформулировать лишь для простейших случаев. В пределе предложения сводятся к описанию фактов, относящихся к отдельным реализациям процесса моделирования, которые назовем прецедентами Рr. Отметим, что Рr составляют эмпирическую основу прикладной теории моделирования, а множество {Рr}, классифицированное по условиям, может рассматриваться как обобщенное предложение теории, содержащее весь зафиксированный в {Рr} опыт моделирования сложных систем вообще.

Более определенные предложения теории могут быть получены на основе системного подхода с детализацией репромодели по этапам построения и реализации S^s и D^s, когда ставятся различные цели при моделировании процессов в системе S. В общем случае репромодель, т. е. ее базис, задается множеством принципов {Пr}, определяющих желаемые свойства моделей (S^s и D^s) и другие ограничения. Использование {Пr} регламентируется предложениями теории, относящимися к ограниченному множеству обобщенных ситуаций. Поиск этих ситуаций в множестве известных {Рr} позволяет накопить необходимые факты в количестве, достаточном для формулировки обобщенных предложений.

Говоря о прикладной теории моделирования с системных позиций, невозможно обойти ее реализационный аспект. В теории это отражено введением понятия трактабельности модели, т. е. ее реализуемости в рамках принятых ресурсных ограничений (например, на оперативную память и быстродействие ЭВМ). Особенно важна трактабельность десиженсных моделей, непосредственно используемых в РИИС, так как часто от нее зависит эффективность конкретного метода и алгоритма управления (а иногда и возможность его использования вообще). Вопросы трактабельности модели ставятся во главу угла при проведении стратегического и тактического планирования машинных экспериментов. Поэтому не будем останавливаться на этих вопросах детально, отметим только, что трактабельность модели достигается выполнением набора практических правил реализации модели {Рr}, которые и составляют тело прикладной теории моделирования.

Таким образом, в конечном итоге множество прецедентов {Рr} выражается через меньшее число эвристических принципов {Пr} и практических правил реализации {Рr} (базис и тело теории). Это позволяет считать репромодель и систему [{Пr}, {Рr}] основой «системного» аспекта прикладной теории моделирования. При практическом применении неизбежно объединение «прецедентного» и «системного» аспектов теории моделирования на основе логического понятия дополнительности. В данном случае это способствует сужению общей проблемы моделирования за счет введения в прикладную теорию компоненты А. Для обеспечения возможности развития репромодель должна строиться как открытая система, т. е. с соблюдением принципов архитектуры открытых систем, что нашло свое отражение при имитационной реализации моделей.

Относительно логики прикладной теории моделирования отметим, что она опирается на индуктивный подход, т. е. обобщение и классификацию множества прецедентов {Рr}, оставляя место для дедуктивного подхода в рамках конкретных математических схем М. Вопросы практического воплощения прикладной теории моделирования непосредственно связаны с реализацией соответствующих инструментальных средств моделирования и возможностью ее использования для решения задач имитационного моделирования конкретных систем.

Основной целью ИМ является прогнозирование в широком смысле этого слова. ИМ позволяет сделать вывод о принципиальной работоспособности объекта (системы S), оценить его потенциально возможные характеристики, установить зависимость характеристик от различных параметров и переменных, определить оптимальные значения параметров и т. п. Имитационные модели М_и, используемые в качестве имитаторов и тренажеров, дают возможность предсказать поведение системы S в условиях взаимодействия с внешней средой Е.

Использование метода ИМ для получения прогноза при принятии решений в системе управления в РМВ времени выдвигает на первое место задачу выполнения ограничения на ресурс времени моделирования процесса функционирования системы S. Для управления объектом может использоваться либо информация о состояниях (ситуациях) системы Sи внешней среды Е, либо информация о выходных характеристиках (поведении) системы Sво взаимодействии с внешней средой Е. Это обстоятельство определяет и цели моделирования. В одном случае требуется оценить изменения состояний z_k Z, k=1,n_z, за время прогнозирования Т_п (назовем такое моделирование ситуационным). В другом случае требуется оценить выходные характеристики z_j Y, j= 1,n_Y, на интервале времени (О, T) (назовем такое моделирование бихевиоральным).

Цель ситуационного моделирования – получение прогноза вектора состояния z (t), а цель бихевиорального моделирования – оценка вектора выходных характеристик у (t). Соответственно целям ситуационного и бихевиорального моделирования должен отличаться и подход к разработке и реализации моделирующих алгоритмов, хотя принципы их построения («принцип t» и «принцип z») сохраняются.

Другой особенностью моделирования для принятия решений по управлению объектом в РМВ является существенная ограниченность вычислительных ресурсов, так как такие системы управления, а, следовательно, и ИМ М_иреализуются, как правило, на базе специализированных микропроцессорных наборов, когда имеется ограничение по быстродействию и объему памяти. Это требует тщательного подхода к минимизации затрат ресурсов по имитационному моделированию в РМВ.

Кроме того, следует учитывать, что достоверность и точность решения задачи моделирования (прогнозирования ситуаций или поведения) системы существенно зависят от количества реализаций N, которые затрачены на получение статистического прогноза. Таким образом, возникает проблема поиска компромисса между необходимостью увеличения затрат времени на моделирование, т. е. числа реализаций N [на интервале (О, Т)]для повышения точности и достоверности результатов моделирования (прогнозирования), и необходимостью уменьшения затрат машинного времени из условий управления в реальном масштабе времени. При использовании имитационной модели М_м в контуре управления системой Sв реальном масштабе времени возникает также проблема оперативного обновления информации как в базе данных об объекте, так и в базе данных об эксперименте, т. е. в данном случае о конкретном прогнозе.

При ситуационном моделировании важно не потерять информацию о смене состояний системы S, так как от этого зависит эффективность управления. Поэтому построение детерминированных моделирующих алгоритмов, когда используется «принцип t», приводит либо к увеличению времени моделирования при уменьшении t, либо к снижению достоверности прогноза состояний при увеличении t. Это говорит в пользу использования стохастических алгоритмов, а именно тех вариантов, которые наиболее просто реализуются, т. е. асинхронных спорадических алгоритмов.

Таким образом, моделирование процесса функционирования систем для целей управления в реальном масштабе времени имеет ряд специфических особенностей, но методика моделирования и принципы реализации моделирующих алгоритмов сохраняются.

Б19 В2

Во многих областях науки и техники важную роль играет понятие иерархии, иерархической структуры. Для таких областей как теория систем, теория управления, типичным является представление объекта исследования (системы) в виде структуры подчиненности одних элементов системы другим. Математической моделью иерархических структур являются ориентированные графы. Ориентированным графом (орграфом) называется кортеж > < E V , , где V – это множество вершин,е(V1?V2 V1?V2 GHBYFL V множество дуг. Присутствие во множестве E вектора ) соответствует наличию связи (дуги) между вершинами 1 v и 2 v графа. Тогда иерархией, или иерархической структурой обычно называют ациклический орграф.

В настоящее время области применения теории графов весьма многочисленны – теория кодирования, нелинейная динамика, управление проектами и т.д. Во многих приложениях графы используются именно для моделирования иерархий, и одной из типичных задач является оптимизация иерархии, то есть поиск оптимальной в некотором смысле иерархической структуры на множестве допустимых иерархий2.

Обычно подобные задачи рассматриваются практически независимо,при их решении существенно используется специфика предметной области. В то же время сходство между этими задачами делает актуальными сведение их к единой постановке и разработку единых подходов к их решению. Основной чертой данного подхода должно быть стремление к рассмотрению задачи оптимизации иерархии в абстрактном виде без привязки к конкретным содержательным интерпретациям. Примерами реализации этой программы служат работы [1-4], и данная статья может 1 Орграф называется ациклическим, если в нем нет циклов – последовательностей дуг вида v1?v2? v3?v4 и т.д.

2 В [6] приведены примеры подобных задач из теории алфавитного кодирования,

теории массового обслуживания, теории управлении

рассматриваться как продолжение намеченной в них программы исследования.

1. Постановка задачи и основные понятия

Как отмечалось выше, задачу оптимизации иерархии можно сформулировать как задачу выбора оптимальной в некотором смысле иерархической структуры из некоторого множества допустимых иерархий (ациклических орграфов).

На практике обычно рассматриваются конечные иерархии, в графе каждой из которых множество вершин конечно. В то же время, анализ бесконечных иерархий иногда позволяет выявить важные свойства оптимальных иерархических структур [5], поэтому далее рассматривается общий случай.

В то же время пока не создано единого методологического подхода к исследованию организационных систем как многоуровневых систем с иерархической структурой. Причем наименее разработанной является проблема синтеза иерархической структуры: поиск структуры общего вида, оптимальной в смысле некоторого критерия. В подавляющем большинстве существующих моделей рассматриваются только древовидные структуры, а ограничения, критерий оптимальности и методы исследования определяются спецификой конкретной задачи. Очевидно, что в общем случае критерий оптимальности может быть произвольным, возможно множественное подчинение, наличие нескольких элементов верхнего уровня

Б19 В3

Статические модели поиска оптимальной структуры предполагают минимизацию некоторого критерия оптимальности на определенном множестве структур. Ключевым моментом при определении статической модели является выбор функционала стоимости. Для различных примеров организационных систем (например, для отраслей промышленности) накоплен огромный эмпирический материал, позволяющий определить некоторые агрегированные параметры структуры. Например, норма управляемости (максимальное число подчиненных) численность управленческого персонала Такие исследования позволяют сравнивать некоторые “типичные” структуры и выбирать из них наиболее подходящую для конкретной системы. Тестирование функционалов на этих “типичных” вариантах позволяет уточнять их вид и параметры, исходя из эмпирических данных и результатов моделирования

Развитие технологии имитационного моделирования. На сегодняшний день имитационное моделирование становится все более зрелой технологией, ее применение в СППР обусловлено созданием развитых многофункциональных оболочек компьютерного моделирования, имеющих средства интеграции с другими интеллектуальными средами. В докладе обозначены основные тенденции в развитии имитационного моделирования, включающие основные аспекты:

 методологический,

 математический,

 технологический.

Развитие методологических основ системного моделирования связано с созданием новых концепций формализации и структуризации моделируемых систем; математической и информационной поддержкой процесса системного моделирования, ориентированной на весь цикл исследования: от постановки проблемы и формирования концептуальной модели – до анализа результатов вычислительного эксперимента и принятия решения; отработкой подходов к созданию стратифицированных описаний моделируемых систем, разработкой методологических подходов к построению СППР и Ситуационных центров, реализацией комплексных проектов по моделированию и многими другими.

Математическая поддержка имитационного моделирования прежде всего связана с широким использованием на разных стадиях имитационного исследования, и в процедурах направленного вычислительного эксперимента, в первую очередь, статистических методов самого различного назначения, математических методов оптимизации и принятия решения, методов искусственного интеллекта.

Технологический уровень современной системы моделирования определяется:

 универсальностью и гибкостью базовой и альтернативной к базовой концепций структуризации и формализации моделируемых динамических процессов, заложенных в систему моделирования. Сегодня популярны среди систем моделирования дискретного типа процессно-ориентированные концепции структуризации, основанные на сетевых парадигмах, автоматном подходе и некоторые другие; среди систем моделирования непрерывного типа – модели и методы системной динамики;

 наличием средств проблемной ориентации, когда система моделирования содержит наборы понятий, абстрактных элементов, языковые конструкции из предметной области соответствующего исследования;

 применением объектно-ориентированных специализированных языков программирования, поддерживающих авторское моделирование и процедуры управления процессом моделирования;

 наличием удобного и легко интерпретируемого графического интерфейса, когда блок-схемы дискретных моделей и системные потоковые диаграммы реализуются на идеографическом уровне, параметры моделей определяются через подменю;

 использованием развитой двух- и трехмерной анимации в реальном времени;

 возможностью для реализации нескольких уровней представления модели, средствами для создания стратифицированных описаний. Стратификация систем, являясь общим принципом системного моделирования, реализуется в технологии имитационного моделирования либо путем детализации, итерационной процедуры эволюции имитационной модели, – либо путем создания комплекса взаимосвязанных моделей, с развитыми информационными и имплицитными связями между моделями. Стратифицированные модели представляют собой машинно-ориентированные понятия, предполагающие конструирование баз данных и знаний, над которыми определены вычислительные процессы решения задач системного анализа и принятия решения. Современные системы моделирования применяют структурно-функциональный подход, многоуровневые иерархические, вложенные структуры и другие способы представления моделей на разных уровнях описания;

 наличием линеек и инструментов для проведения и анализа результатов сценарных, вариантных расчетов на имитационной модели;

 математической и информационной поддержкой процедур анализа входных данных, анализа чувствительности и широкого класса вычислительных процедур [3], связанных с планированием, организацией и проведением направленного вычислительного эксперимента на имитационной модели. Специализированные аналитические блоки на основе методов планирования факторного эксперимента, дисперсионного, регрессионного анализа и широкого спектра статистических методов [5], методологии анализа поверхности отклика и другими блоками оптимизации, ориентированными на специфику имитационного моделирования не исчерпывают весь инструментарий аналитической поддержки направленного вычислительного эксперимента на имитационной модели. Перспективно применение итерационных имитационно-оптимизационных процедур [6], балансовых методов и логистических процедур, логических методов принятия решения [7], экспертных систем и методов искусственного интеллекта при организации и обработке результатов эксперимента на имитационной модели. Экспериментальные исследования на имитационной модели информативны, поэтому необходима реализация подхода Simulation Data Base, основанного на доступе к базам данных моделирования. Технологически это решается при помощи собственных специализированных аналитических блоков системы моделирования или за счет интеграции с другими программными средами;

 применением многопользовательского режима работы, интерактивного распределенного моделирования, разработками в области взаимодействия имитационного моделирования со Всемирной паутиной и др.