Свойства нечетких множеств

Определение 12.Высотой нечеткого множества называется верхняя граница его функции принадлежности: . Для дискретного универсального множества супремум становится максимумом, а значит высотой нечеткого множества будет максимум степеней принадлежности его элементов

Определение 13.Нечеткое множество называется нормальным, если его высота равна единице. Нечеткие множества не являющиеся нормальными называются субнормальными. Нормализация ‑ преобразование субнормального нечеткого множества в нормальное определяется так: . В качестве примера на рис. 1 показана нормализация нечеткого множества с функцией принадлежности .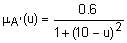

Рисунок 1 - Нормализация нечеткого множества

Определение 14.Носителем нечеткого множества называется четкое подмножество универсального множества , элементы которого имеют ненулевые степени принадлежности: .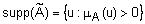

Определение 15.Нечеткое множество называется пустым, если его носитель является пустым множеством.

Определение 16.Ядром нечеткого множества называется четкое подмножество универсального множества , элементы которого имеют степени принадлежности равные единице: . Ядро субнормального нечеткого множества пустое.

Определение 17. -сечением (или множеством -уровня)нечеткого множества называется четкое подмножество универсального множества , элементы которого имеют степени принадлежности большие или равные : 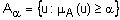, . Значение называют -уровнем. Носитель (ядро) можно рассматривать как сечение нечеткого множества на нулевом (единичном) -уровне.

Рис. 2 иллюстрирует определения носителя, ядра, -сечения и -уровня нечеткого множества.

Рисунок 2 - Ядро, носитель и -сечение нечеткого множества

Определение 18.Нечеткое множество называется выпуклым если: , , . Альтернативное определение: нечеткое множество будет выпуклым, если все его -сечения - выпуклые множества. На рис. 3 приведены примеры выпуклого и невыпуклого нечетких множеств.

Рисунок 3 - К определению выпуклого нечеткого множества Определение 19.Нечеткие множества и равны ( ) если .