
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ускорение.
Ускорение- векторная физическая величина, характеризующая быстроту изменения скорости 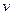 .
.
Ускорением называется вектор 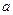 , равный первой производной по времени
, равный первой производной по времени 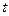 от скорости
от скорости 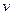 этой точки. Ускорение точки также равно второй производной по времени от радиуса-вектора
этой точки. Ускорение точки также равно второй производной по времени от радиуса-вектора 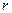 этой точки:
этой точки:
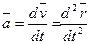 .
.
Разложение ускорения точки по базису  , то есть на составляющие по осям прямоугольной декартовой системы координат, имеет вид:
, то есть на составляющие по осям прямоугольной декартовой системы координат, имеет вид:
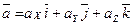 , где
, где
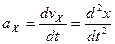 ,
,  ,
, 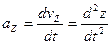 .
.
Здесь  ,
, 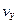 ,
, 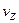 - компоненты скорости точки, а
- компоненты скорости точки, а 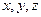 - координаты точки в рассматриваемый момент времени.
- координаты точки в рассматриваемый момент времени.
Если траектория точки- плоская кривая, то ускорение 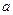 точки лежит в этой плоскости. В общем случае траектория точки- пространственная кривая, а ускорение
точки лежит в этой плоскости. В общем случае траектория точки- пространственная кривая, а ускорение 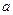 лежит в соприкасающейся плоскости. В соприкасающейся плоскости есть два избранных направления- касательной к траектории (орт
лежит в соприкасающейся плоскости. В соприкасающейся плоскости есть два избранных направления- касательной к траектории (орт 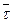 ) и главной нормали (орт
) и главной нормали (орт  ). Поэтому вектор
). Поэтому вектор 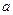 удобно разложить на две составляющие вдоль этих направлений, то есть по базису
удобно разложить на две составляющие вдоль этих направлений, то есть по базису 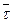 , n:
, n:
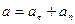
Составляющая  называется касательным или тангенциальным ускорением точки, а составляющая
называется касательным или тангенциальным ускорением точки, а составляющая 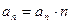 - нормальным ускорением точки.
- нормальным ускорением точки.
Для нахождения значений  и
и  компонент вектора
компонент вектора 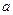 воспользуемся выражением для скорости точки
воспользуемся выражением для скорости точки 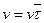 . Следовательно,
. Следовательно,
 .
.
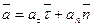
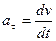 .
.
 При перемещении по траектории на малое расстояние
При перемещении по траектории на малое расстояние 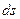 единичный вектор касательной поворачивается на угол
единичный вектор касательной поворачивается на угол 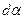 . Из равнобедренного треугольника векторов видно, что ввиду малости
. Из равнобедренного треугольника векторов видно, что ввиду малости 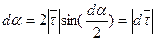 , а по направлению вектор
, а по направлению вектор 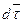 совпадает с ортом главной нормали
совпадает с ортом главной нормали  . Таким образом:
. Таким образом:
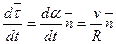
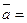
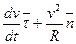 .
.
Дата добавления: 2015-01-19; просмотров: 286; Мы поможем в написании вашей работы!; Нарушение авторских прав |