Момент пары сил.

Парой называются силы равные по величине, противоположные по направлению, но не действующие по одной прямой.

Момент пары сил не зависит от выбора оси

( -плечо пары сил).

Момент импульса:

- материальной точки относительно неподвижной точки

Моментом импульса 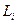материальной точки относительно неподвижной точки 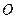называется векторное произведение радиуса-вектора материальной точки, проведенного из точки O, на импульс этой материальной точки

- системы материальных точек относительно неподвижной точки

Моментом импульса механической системы относительно неподвижной точки 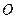называется вектор равный геометрической сумме моментов импульса относительно той же точки всех материальных точек системы.

- материальной точки относительно неподвижной оси.

- системы материальных точек относительно неподвижной оси.

Моментом импульса механической системы относительно оси называется проекция на эту ось вектора момента импульса системы относительно любой точки, выбранной на рассматриваемой оси.

БИЛЕТ 13. Момент инерции относительно оси. Теорема Штейнера. Примеры расчета момента инерции.

Величина 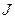, равная сумме произведений масс всех материальных точек , образующих механическую систему, на квадраты их расстояний от данной оси, называется моментом инерции системы относительно этой оси.

Момент инерции:

Материальной точки Системы материальных точек Абсолютно твердого тела

Таким образом, момент импульса тела относительно оси ОZ равен

Теорема Штейнера:

Момент инерции 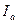тела относительно произвольной оси 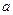равен сумме моментов инерции тела относительно параллельной ей оси ,

проходящей через центр масс тела и произведения массы тела 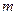на квадрат расстояния между этими осями.

Доказательство:

На рисунке ос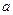и и направлены перпендикулярно плоскости чертежа, а расстояния от малого элемента тела массой до этих осей обозначены соответственно 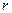и . По теореме косинусов:

где - абсцисса элемента тела в системе координат с началом в центре масс тела и осью абсцисс, пересекающей ос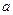и и и лежащей в перпендикулярной им плоскости. Из определения центра масс следует, что

так как центр масс совпадает с началом координат . Справедливость соотношения доказана.

Примеры расчета момента инерции.