
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Система материальных точек.







Импульсом системы материальных точек назовем векторную сумму импульсов всех материальных точек системы


БИЛЕТ 5. Центр масс. Теорема о движении центра масс.
Центром масс (центром инерции) системы материальных точек называется точка  , радиус вектор которой равен отношению суммы произведений масс всех материальных точек системы на их радиусы-векторы к массе всей системы.
, радиус вектор которой равен отношению суммы произведений масс всех материальных точек системы на их радиусы-векторы к массе всей системы.
 ,
,
где  и
и  - масса и радиус-вектор
- масса и радиус-вектор  -й материальной точки,
-й материальной точки,  и
и  - общее число этих точек в системе и ее суммарная масса.
- общее число этих точек в системе и ее суммарная масса.
В частности, если радиусы-векторы проведены из центра масс  (обозначим их
(обозначим их  ), то
), то

Таким образом, центр масс- это геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиусы-векторы, проведенные из этой точки, равна нулю.
Координаты центра масс системы:



В случае непрерывного распределения массы в системе (например, в случае протяженного тела) радиус-вектор центра масс системы
 ,
,
где 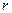 - радиус-вектор малого элемента системы, масса которого равна
- радиус-вектор малого элемента системы, масса которого равна  , а интегрирование производится по всем элементам системы, то есть по всей ее массе
, а интегрирование производится по всем элементам системы, то есть по всей ее массе 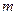 .
.

Соответственно импульс системы равен произведению ее массы на скорость центра масс  . Получаем закон движения центра масс:
. Получаем закон движения центра масс:

Центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору приложения к системе внешних сил.
Этот закон показывает, что для изменения скорости центра масс системы необходимо, чтобы на систему действовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызвать изменения скоростей этих частей (например при разрыве снаряда не несколько частей), но они не могут повлиять на суммарный импульс системы и на скорость ее центра масс.
БИЛЕТ 6. Закон сохранения импульса. Абсолютно неупругий удар.
На замкнутую систему внешние силы не действуют. Поэтому из закона изменения импульса вытекает закон сохранения импульса:Импульс замкнутой системы не изменяется с течением времени.
 и
и 
где  и
и  - масса и скорость
- масса и скорость  -й материальной точки системы, состоящей из n точек.
-й материальной точки системы, состоящей из n точек.
Соответственно не изменяются также и проекции импульса замкнутой системы на оси декартовых координат инерциальной системы отсчета:



Импульс системы  , где
, где 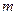 - масса всей системы, а
- масса всей системы, а  - скорость ее центра масс. Поэтому из закона сохранения импульса следует, что при любых процессах, происходящих в замкнутой системе, скорость ее центра масс не изменяется.
- скорость ее центра масс. Поэтому из закона сохранения импульса следует, что при любых процессах, происходящих в замкнутой системе, скорость ее центра масс не изменяется.
Рассмотрим применение закона сохранения импульса к расчету абсолютно неупругого прямого центрального удара двух тел. Ударом называется явление изменения скоростей тел на конечные значения за очень короткий промежуток времени, происходящее при их столкновениях В процессе удара возникают кратковременные ударные силы взаимодействия между сталкивающимися телами, причем эти силы во много раз превосходят все внешние силы, действующие на тела. Поэтому в процессе удара систему соударяющихся тел можно приближенно считать замкнутой и применять к ней закон сохранения импульса. Общая нормаль к поверхности соударяющихся тел в точке их соприкосновения называется линией удара. Удар называется прямым, если перед ударом скорости центров масс соударяющихся тел параллельны линии удара. Удар называется центральным, если центры масс соударяющихся тел лежат на линии удара. Прямой центральный удар называется абсолютно неупругим, если после удара тела движутся как одно целое, т. е. с одной и той же скоростью. Бели скорости тел до удара равны  и
и 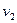 , а их массы равны
, а их массы равны 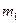 и
и 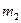 , то в соответствии с законом сохранения импульса общая скорость поступательного движения этих тел после абсолютно неупругого прямого центрального удара равна
, то в соответствии с законом сохранения импульса общая скорость поступательного движения этих тел после абсолютно неупругого прямого центрального удара равна

При неупругом ударе происходят различного рода процессы в соударяющихся телах (их пластические деформации, трение и др.), в результате которых кинетическая энергия системы частично преобразуется в ее внутреннюю энергию, т. е. происходит диссипация механической энергии системы.
Изменение кинетической энергии системы двух сталкивающихся тел при абсолютно неупругом прямом центральном ударе равно

Для абсолютно неупругого удара:
 и
и  (часть механической энергии системы переходит во внутреннюю энергию
(часть механической энергии системы переходит во внутреннюю энергию  )
)







БИЛЕТ 7. Работа. Мощность. Кинетическая энергия. Закон изменения кинетической энергии.
Изменение механического движения тела и, следовательно, его механической энергии происходит в процессе механического действия на рассматриваемое тело со стороны других тел. Мерой этого действия служат соответствующие силы. Поэтому следует говорить об изменении механической энергии тела под влиянием приложенных к нему сил. Для количественного описания такого процесса изменения энергии тела вводят в механике понятие работы силы.
Элементарной работой  силы
силы 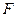 на малом перемещении
на малом перемещении 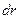 точки
точки  приложения силы называется скалярное произведение
приложения силы называется скалярное произведение 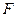 на
на 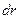 :
:
 =
= 
где 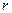 и
и  - радиус-вектор и скорость точки
- радиус-вектор и скорость точки  ,
,  - малый промежуток времени в течение которого сила
- малый промежуток времени в течение которого сила 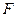 совершает работу
совершает работу  .
.
Так как скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними, то
 =
= 
где  - путь точки
- путь точки  за малое время
за малое время  ,
,  -угол между силой
-угол между силой 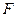 и элементарным перемещением
и элементарным перемещением 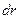 (или скоростью
(или скоростью 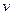 ) точки
) точки  ,
, 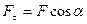 - проекция силы
- проекция силы 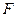 на направление
на направление 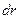 (или
(или 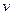 ).
).
Сила не совершает работы в двух случаях:
1). Точка приложения силы неподвижна ( 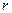 =const, а
=const, а 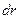 =0)
=0)
2). Угол  , то есть сила
, то есть сила 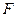 направлена по нормали к траектории точки ее приложения.
направлена по нормали к траектории точки ее приложения.  .
.
Если угол  острый, то сила движущая, если тупой, то тормозящая.
острый, то сила движущая, если тупой, то тормозящая.
Согласно правилу скалярного умножения векторов, элементарная работа силы 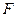 в декартовых координатах равна:
в декартовых координатах равна:
 =
= 
Работа, совершаемая силой 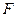 на конечном перемещении точки ее приложения из положения 1 в положение 2 равна сумме элементарных работ силы на всех малых участках траектории от точки 1 до точки 2. Эта сумма приводится к интегральной:
на конечном перемещении точки ее приложения из положения 1 в положение 2 равна сумме элементарных работ силы на всех малых участках траектории от точки 1 до точки 2. Эта сумма приводится к интегральной:
 .
.
Работа при прямолинейном движении равна:  и численно равна площади под графиком.
и численно равна площади под графиком.

Работа потенциальной силы на произвольной замкнутой траектории  точки ее приложения равна нулю.
точки ее приложения равна нулю.


Дата добавления: 2015-01-19; просмотров: 359; Мы поможем в написании вашей работы!; Нарушение авторских прав |