Закон изменения кинетической энергии.

Изменение кинетической энергии равно сумме работ, совершаемых при этом всеми внешними и внутренними силами:

,

причем сумму элементарных работ 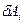всех сил, приложенных к 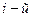материальной точке системы удобно разбить на две части:

.

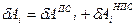БИЛЕТ 8. Консервативные и неконсервативные силы. Потенциальная энергия. Связь потенциальной энергии с силой. Потенциальная энергия тела в положении равновесия.

Сила F, действующая на материальную точку М называется потенциальной (консервативной), если работа этой силы зависит только от начального и конечного положений точки М.

(Пример: гравитационные силы и силы упругости)

Диссипативными (неконсервативными) называются силы, зависящие от скоростей точек механической системы и совершающие отрицательную суммарную работу при любых перемещениях этой системы.

(Пример: силы трения скольжения, силы сопротивления движению).

Работа , совершаемая потенциальными силами при изменении конфигурации системы, то есть расположения ее частей (материальных точек) относительно системы отсчета, не зависит от того, как конкретно осуществляется процесс перехода из начальной конфигурации системы (1) в конечную (2). Работа полностью определяется начальной и конечной конфигурацией системы. Следовательно, ее можно представить в виде разности значений некоторой функции конфигурации системы 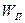, называемой потенциальной энергией системы:

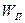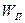= (1)- (2).

Соответственно элементарная работа потенциальных сил при малом изменении конфигурации системы

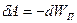
Если внешние потенциальные силы нестационарны, то потенциальная энергия системы зависит не только от конфигурации системы, но также и от времени 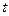. Между тем работу эти силы совершают только при перемещении системы. Поэтому данное соотношение справедливо лишь при условии стационарности внешних потенциальных сил. В общем случае:

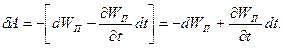
Член показывает, как изменяется за малое время потенциальная энергия системы при условии, что конфигурация системы остается одной и той же. Измеряя работу потенциальных сил, приложенных к системе, можно найти только разность значений потенциальной энер­гии этой системы в двух ее состояниях: начальном и конечном. Иначе говоря, потенци­альную энергию системы можно найти только с точностью до произвольного постоян­ного слагаемого. В каждой конкретной задаче для получения однозначной зависимости потенциальной энергии рассматриваемой системы от ее конфигурации выбирают нуле­вую конфигурацию, в которой потенциальную энергию системы полагают равной нулю. Таким образом, потенциальной энергией механической системы называется вели­чина, равная работе, которую совершают все действующие на систему потенциальные силы при переводе системы из рассматриваемого состояния в состояние, соответст­вующее ее нулевой конфигурации.

Рассмотрим простейшую механическую системы, состоящую из одной материальной точки, на которую действует потенциальная сила F.

Так как координаты точки х, у, z — независимые переменные, то в последнем уравне­нии должны быть попарно равны слева и справа коэффициенты при dx, dy и dz. Таким образом, связь между потенциальной энергией материальной точки и соответствующей ей потенциальной силой F имеет

вид:

= , = , = ,

или

Вектор, стоящий в квадратных скобках и построенный с помощью скалярной функции 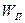, называется градиентом функции 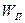и обозначается grad .

.

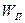Вид формулы потенциальной энергии зависит от характера взаимодействия тел.

Например, сила тяжести: , сила упругости .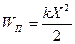

Изменить 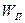могут гравитационные силы и силы упругости (в электростатике еще и кулоновские силы). Работа этих сил по замкнутой траектории всегда равна нулю. Такие силы называют консервативными.