Дискретная случайная величина. Закон распределения.

Ответ: Реальное содержание понятия «случайная величина» может быть выражено с помощью такого определения: случайной величиной, связанной с данным опытом, называется величина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, причем заранее неизвестно, какое именно. Случайные величины будем обозначать буквами Определение. Говорят, что задана дискретная случайная величина , если указано конечное или счетное множество чисел

и каждому из этих чисел поставлено в соответствие некоторое положительное число , причем: Числа называются возможными значениями случайной величины , а числа 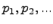- вероятностями этих значений ( ). Таблица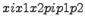

называется законом распределения дискретной случайной величины . Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины . Если возможными значениями дискретной случайной величины являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли: то говорят, что случайная величина имеет биномиальный закон распределения: 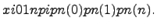Пусть заданы натуральные числа m, n, s, причем Если возможными значениями дискретной случайной величины являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле: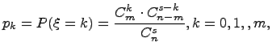

то говорят, что случайная величина имеет гипергеометрический закон распределения.

Другими часто встречающимися примерами законов распределения дискретной случайной величины являются: геометрический: где ; Закон распределения Пуассона: где: - положительное постоянное. Закон распределения Пуассона является предельным для биномиального при , , 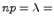. Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона: где .