
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вероятность попадания непрерывной случайной величины в заданный интервал. Ответ: Равномерный закон распределения
Ответ: Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, т.е. f(x) имеет вид:

| 
| 
| 
| 
| |||
| Функция плотности вероятности f(x) | Функция плотности вероятности f(x) | Функция распределения F(x) | |||||
| Рис.1. Равномерный закон распределения | Рис.1. Равномерный закон распределения | ||||||
Математическое ожидание:  . Математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка. Дисперсия:
. Математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка. Дисперсия:

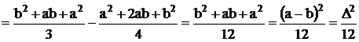 Величина
Величина  называется поправкой Шеппарда. Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]:
называется поправкой Шеппарда. Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]: 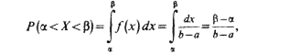

|
Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения иоднозначно определяют равномерное распределение. Пример 4. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины.

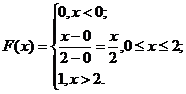
Дата добавления: 2015-01-19; просмотров: 316; Мы поможем в написании вашей работы!; Нарушение авторских прав |